DSP定点运算学习路线图：系统性掌握定点数运算的必备知识


# 摘要
随着数字信号处理技术的广泛应用，定点运算在DSP系统中的重要性日益凸显。本文首先介绍了DSP定点运算的基本概念及其数学基础，阐述了定点数与浮点数的区别和定点数的表示、运算规则以及转换原理。接着，文章深入探讨了定点数在DSP编程中的实现方法，包括C语言中的定点数编程技巧和DSP处理器的指令集优化，同时对定点数运算的性能进行评估。此外，本文还分析了定点数运算在DSP系统中的应用案例，如滤波器设计和图像处理，并探讨了音频及视频处理中定点数的具体运用。最后，文章着眼于定点运算的进阶话题，包括精度分析、定点数与深度学习的结合，以及优化算法的研究，为未来的DSP定点运算研究和应用提供了新的视角和方法。

# 关键字
DSP定点运算；定点数表示；定点数运算；性能评估；滤波器设计；图像处理；深度学习

参考资源链接：[DSP定点运算详解：数的定标与Q/S表示法](https://wenku.csdn.net/doc/5yn7kromu1?spm=1055.2635.3001.10343)
# 1. DSP定点运算简介

在数字信号处理（DSP）领域，定点运算是一种重要的技术，它对于理解DSP硬件和软件的实现至关重要。相对于浮点运算，定点运算由于其简单性和高效性，在实时系统中被广泛应用。本章将介绍定点运算的基本概念和重要性，为读者提供一个全面的概述。

## 1.1 定点运算的定义和优势
定点运算指的是使用整数进行运算，以表示数字信号处理中的各个参数和中间结果。其优势在于占用的存储资源较少，运算速度更快，这对于硬件要求严格的嵌入式系统而言，是非常必要的。

## 1.2 定点运算在DSP中的应用
在数字信号处理中，如滤波、编码解码等操作，都依赖于高效的定点数计算。定点运算是实现实时信号处理的基础，同时它也优化了算法的执行速度和资源消耗。

随着技术的进步，定点运算是现代DSP设计和应用中的一个核心话题。下一章节，我们将深入探讨定点数的基本概念和表示方法。

# 2. 定点数的基本概念

定点数是计算机科学与数字信号处理中的基础概念，广泛应用于各类数字系统中。相较于浮点数，定点数在资源受限的环境（例如嵌入式系统或硬件加速器）中有着性能上的优势。本章深入探讨了定点数与浮点数的区别、定点数的表示方式、定点数的运算规则以及定点数与浮点数之间的转换方法。

### 2.1 数学基础与定点表示法

#### 2.1.1 定点数与浮点数的区别

在计算机中，数值的表示方法主要有定点数和浮点数两种。浮点数的表示基于科学计数法，通过一个尾数（mantissa）、基数（一般为2）和指数（exponent）来表示一个数。这种表示方法可以覆盖很大范围的数值，但相对于定点数需要更多的硬件资源和运算时间。

定点数则使用固定的小数点位置来表示数值，这个位置不会变动。定点数在进行运算时，小数点位置保持不变，因此定点运算可以更加高效。定点数的运算比浮点数更快，因为其运算规则更简单，不需要处理尾数和指数的动态变化。但是，定点数表示数值的范围受限，当数值超出其表示范围时，就会发生溢出。

#### 2.1.2 定点数的表示与范围

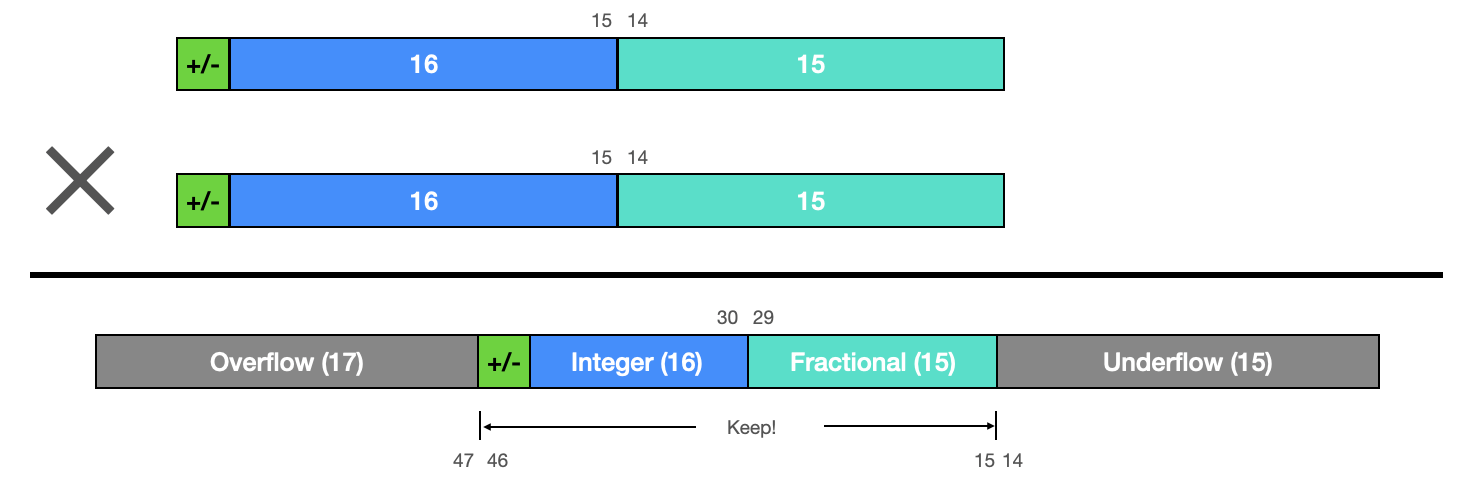
定点数的表示包括整数部分和小数部分，通常采用Q格式来描述。Q格式是一种符号-值表示法，例如Q15表示一个16位的数，其中最高位为符号位，剩余的15位用于表示数值。Q格式将数值分为整数部分和小数部分，小数点的位置根据Q值的不同而固定。

定点数的表示范围和精度取决于其占用的位数和小数点的位置。Q格式的具体表示能力可以通过以下公式计算：

表示范围 = [-2^(n-1), 2^(n-1) - 1] 或 [-(2^(n-1) - 1), 2^(n-1)]
精度 = 1 / 2^m

这里，n为定点数的位数（包括符号位），m为小数部分的位数。

### 2.2 定点数的运算规则

#### 2.2.1 四则运算

定点数的四则运算遵循数学的基本规则，但有其特殊性。例如，加减法运算时，需要确保两个数的小数点对齐，这意味着在运算前可能需要对操作数进行适当的移位操作。乘法运算中，定点数相乘后的结果位数会增加，因此需要通过截断或舍入的方式恢复到定点数的原始位宽。除法则通常通过乘以倒数的方式来实现。

#### 2.2.2 乘法与除法的截断处理

在进行定点数乘法时，结果的位宽为两个操作数位宽之和。如果结果位宽超过了定点数原有的位宽，必须进行截断以适应Q格式的规定。截断过程通常涉及舍入到最接近的定点数。

除法是四则运算中最复杂的，因为除法运算可能会导致无限循环小数的情况。在定点数系统中，除法常常通过乘以一个近似值来实现，或者转换为一个可逆的乘法运算。例如，除以一个数等价于乘以它的倒数。由于乘法运算通常比较快速，因此除法运算经过这种转换后可以实现更高效的处理。

### 2.3 定点数与浮点数的转换

#### 2.3.1 转换原理

定点数与浮点数之间的转换是一种常见的需求，尤其是在需要与其他使用浮点数的系统或算法交互时。转换的过程需要考虑到数值的范围和精度损失。转换通常通过乘除操作和移位操作来实现，有时还会引入舍入误差。

#### 2.3.2 转换中的舍入误差分析

舍入误差是定点数转换过程中难以避免的。由于定点数的表示范围和精度都是有限的，当数值太大或太小无法用定点数表示时，就需要通过舍入到最接近的可表示数值。这可能会引入误差，特别是在多次运算累积误差时。为了控制误差，通常需要预先分析误差传播特性，并在设计定点算法时考虑误差控制策略。

在本章中，我们深入理解了定点数的基础概念和相关数学原理，为后续章节深入定点数的编程实现、应用实践以及优化策略打下了坚实的基础。通过具体案例和详细的技术分析，我们将在后续章节中探讨定点数在DSP系统中的实际应用，以及如何针对这些应用进行有效的编程实践和性能优化。

# 3. 定点数的编程实现

## 3.1 C语言中的定点数编程
### 3.1.1 数据类型的选用
在C语言中，定点数的实现主要依赖于整数类型，因为定点数的运算可以通过整数运算来模拟。整数类型的选择将影响到定点数表示的范围和运算精度。例如，在嵌入式系统或DSP应用中常用的有`int16_t`和`int32_t`，这些类型分别表示16位和32位的有符号整数。

### 3.1.2 编译器优化与定点数操作
编译器的优化设置对定点数的性能影响很大。在C语言中使用定点数时，应当充分理解并利用编译器的优化指令，例如GCC编译器中的`-O2`和`-O3`优化选项。此外，还可以使用特定的编译器指令，如`__builtin_clz`（计算前导零的数量），以提高定点数运算的效率。

int16_t multiply(int16_t a, int16_t b) {
    // 无符号扩展乘法，编译器可能优化
    return (int16_t)((uint32_t)a * (uint32_t)b >> 16);
}

在上述代码中，`multiply`函数用于计算两个16位定点数的乘积。代码使用无符号扩展，以避免溢出，并将结果右移16位来恢复定点表示。编译器可能对这种模式的乘法进行优化。

## 3.2 DSP处理器的定点数指令集
### 3.2.1 指令集概览
DSP处理器提供了专门的指令集来执行定点数运算，这些指令集通常包括了对定点数的高效处理。例如，TI（德州仪器）的C6000系列DSP提供了多条专门用于定点数运算的指令，如MPY（乘法）、ADD（加法）等。

### 3.2.2 优化定点运算的指令使用
在DSP中使用定点运算指令时，应当考虑指令流水线和并行处理能力，从而达到最优的性能表现。例如，C