【数据分析核心算法】：深入Origin矩阵转置算法与应用


# 摘要
本论文全面探讨了矩阵转置的概念、理论基础及其在数据分析中的应用。首先介绍了矩阵转置的基本概念和理论，包括矩阵的定义、分类、转置的数学原理及算法复杂度分析。其次，详细阐述了Origin软件中的矩阵转置算法，包括算法流程、关键技术点以及优化策略，并对其性能进行了评估。通过数据预处理与矩阵构建，进一步探讨了矩阵转置在数据特征提取、变换和降维技术中的应用。在进阶应用章节中，研究了高级矩阵转置技术，探讨了其与机器学习算法的结合以及大数据分析环境下的挑战和应对策略。最后，论文总结了矩阵转置算法的关键原理和实践应用，并展望了其未来的发展方向。

# 关键字
数据分析；矩阵转置；理论基础；算法复杂度；Origin软件；并行计算；机器学习；大数据分析

参考资源链接：[Origin入门：详细教程——矩阵转置与工作环境设置](https://wenku.csdn.net/doc/5mxv9nf4ba?spm=1055.2635.3001.10343)
# 1. 数据分析与矩阵转置的基本概念

数据分析在现代社会扮演着越来越重要的角色，无论是商业决策、科学研究，还是工程应用，数据分析都提供着洞察力与预测能力。矩阵转置是数据分析中不可或缺的一个环节，它涉及到数据结构的转换，是许多复杂算法的基础。矩阵转置本质上是对矩阵行列进行交换，但其背后的数学意义和应用价值远远超出了这一简单操作。本章将带你了解数据分析的基础概念，并深入解析矩阵转置的基本定义、重要性以及它在数据分析中的作用。

# 2. 矩阵转置的理论基础

### 2.1 矩阵的基本性质

#### 2.1.1 矩阵定义及分类
矩阵是由数或表达式构成的矩形阵列。在数学中，矩阵可以表示线性变换和系统中的线性关系。矩阵中的元素可以是实数、复数、甚至可以是矩阵本身，从而形成高阶矩阵。矩阵根据其元素类型和维度大小进行分类，常见的有以下几种：

- 方阵：行数和列数相等的矩阵，具有行列式这一重要性质。
- 零矩阵：所有元素均为零的特殊矩阵。
- 单位矩阵：主对角线上元素为1，其余为0的方阵。
- 对角矩阵：主对角线以外的元素均为零的方阵。
- 稀疏矩阵：大部分元素为零的矩阵，常在科学计算中出现。
- 稠密矩阵：大部分非零元素的矩阵。

| 矩阵类型       | 特征描述                             |
| -------------- | ------------------------------------ |
| 方阵           | 行数和列数相等的矩阵                 |
| 零矩阵         | 所有元素均为零的矩阵                 |
| 单位矩阵       | 主对角线上元素为1，其余为0的方阵     |
| 对角矩阵       | 主对角线以外的元素均为零的方阵       |
| 稀疏矩阵       | 大部分元素为零的矩阵                 |
| 稠密矩阵       | 大部分非零元素的矩阵                 |

在进行矩阵转置时，以上类型矩阵的性质会影响转置算法的复杂度和实现方式。例如，对角矩阵转置后仍然为对角矩阵，而稀疏矩阵的转置则需优化存储和计算过程以提升效率。

#### 2.1.2 矩阵转置的数学原理
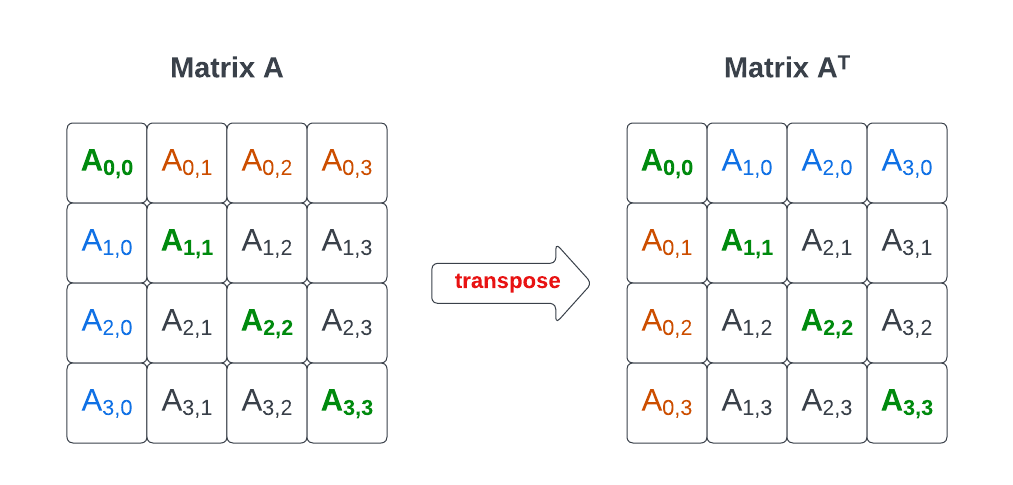
矩阵转置是将矩阵的行换成列，列换成行的操作。对于一个m×n的矩阵A，其转置记为A^T，是一个n×m的矩阵，矩阵中元素a_ij在转置后变为a_ji。

矩阵转置的基本性质如下：

- (A^T)^T = A
- (A + B)^T = A^T + B^T
- (kA)^T = kA^T，其中k是标量。
- (AB)^T = B^T A^T
- 若A可逆，则(A^T)^(-1) = (A^(-1))^T

### 2.2 矩阵运算与算法复杂度

#### 2.2.1 矩阵的基本运算规则
矩阵运算包括加法、减法、数乘、乘法、求逆等，转置作为一种特殊的矩阵运算，其计算规则相对简单。具体而言，矩阵转置过程中，原矩阵的第i行第j列元素在转置矩阵中变为第j行第i列元素。

例如，设有矩阵A：

| 1  2  3 |
| 4  5  6 |

A转置后表示为A^T：

| 1  4 |
| 2  5 |
| 3  6 |

#### 2.2.2 算法复杂度分析
在进行矩阵转置算法复杂度分析时，通常关注时间复杂度和空间复杂度。对于一个m×n的矩阵A，标准转置算法的时间复杂度为O(mn)，这是因为每个元素都需要从其原始位置移动到新位置。

对于稀疏矩阵或块矩阵，可以通过特定的数据结构如压缩行存储(CRS)或压缩列存储(CCS)来降低时间复杂度和空间复杂度。例如，在块矩阵转置中，如果每个块内部已经是转置好的，则整个矩阵转置可以通过交换块的顺序实现，其时间复杂度通常会低于O(mn)。

### 2.3 矩阵转置在数据分析中的重要性

#### 2.3.1 数据处理中的矩阵应用
在数据分析中，矩阵常用于表示数据集中的数据点和特征。例如，在机器学习的特征工程中，特征矩阵就是用于训练模型的数据结构。矩阵转置在数据预处理阶段尤为重要，因为它可以帮助我们将数据的维度从宽格式转换为长格式，反之亦然。

举例而言，考虑以下宽格式的CSV文件，记录了某几个人的身高、体重和年龄：

| Name | Height | Weight | Age |
| ---- | ------ | ------ | --- |
| Tom  | 180    | 70     | 30  |
| Bob  | 175    | 65     | 28  |

在很多数据分析工具中，如Python的pandas库，这些数据通常以二维矩阵形式展示，每个特征成为一列。若要将每个特征视为一个观测值，我们需要将矩阵转置。

#### 2.3.2 矩阵转置对算法效率的影响
在某些情况下，矩阵转置可以作为一种算法优化的手段。比如，在矩阵乘法中，如果输入矩阵的维度不匹配，先进行转置操作可能会产生更小的中间矩阵，从而减少乘法过程中的计算量和存储空间。

例如，设矩阵A的维度为m×n，矩阵B的维度为n×p，其乘法结果C的维度为m×p。如果A或B中的一个矩阵为非方阵且非常大，直接相乘可能很耗时。但如果先对其中一个矩阵进行转置，可能会使得两个矩阵的乘法更高效。

import numpy as np

A = np.random.rand(1000, 500)  # 1000x500 矩阵
B = np.random.rand(500, 200)   # 500x200 矩阵

# 直接乘法
C = np.dot(A, B)  # 时间复杂度为O(mnp)

# A转置后乘法
A_T = A.T
C_T = np.dot(B.T, A_T)  # 时间复杂度可能降低

通过上述代码示例，我们可以看到在矩阵乘法操作中引入转置可能会改变计算量。特别是当m远大于p时，转置B矩阵后，其维度变为200x500，可能能降低时间复杂度。

转置操作在算法中的效率提升通常依赖于具体问题和上下文。因此，对于数据科学家和工程师而言，理解矩阵转置的原理及其在算法中的应用是实现高效计算的关键。

# 3. Origin矩阵转置算法详解

## 3.1 Origin软件概述

### 3.1.1 Origin软件功能与应用领域

Origin 是一款专业的科学绘图和数据分析软件，它广泛应用于物理学、化学、工程学、生物学等领域。软件提供了一整套丰富的工具和功能，包括数据处理、统计分析、信号处理、图像分析以及二维和三维图形绘制等。Origin 的灵活性和强大的数据处理能力使其成为科研人员和工程师不可或缺的工具。

在 Origin 中，用户可以通过内置的函数、公式和脚本语言，对数据进行各种复杂的处理。此外，Origin 支持多种数据导入格式，并且可以导出为多种格式，便于与其他应用程序交互和报告结果。

### 3.1.2 Origin中的矩阵操作

Origin 中的矩阵操作功能特别强大，用户可以通过其内置的矩阵函数和方法，对数据进行矩阵级的运算。Origin 支持矩阵的创建、编辑、转置、乘法、加法等基本操作。在数据分析过程中，Origin 也提供了高级矩阵操作，如矩阵分解、特征值计算、矩阵运算符重载等，这些功能对于需要进行数值计算和工程计算的用户非常有用。

在 Origin 中，矩阵操作通常可以通过菜单、工具栏按钮或是通过内置的 LabTalk 脚本语言和 Origin C 编程语言来执行。

## 3.2 Origin矩阵转置算法流程

### 3.2.1 算法步骤分析

Origin 的矩阵转置算法是一个直接且高效的过程。要对一个矩阵进行转置，用户首先需要在 Origin 中选择或创建一个矩阵对象。接着，用户可以通过点击矩阵操作工具栏中的“转置”按钮，或者使用 Ori