【科学实验数据处理】：Origin转置矩阵在实验分析中的关键作用


# 摘要
Origin软件以其强大的数据处理能力在科研领域广泛应用，其中矩阵操作是其核心功能之一。本文详细介绍了Origin软件中矩阵转置的理论基础、应用方法和在实验数据分析中的高级技巧。首先，从矩阵转置的定义和数学原理出发，阐述了其在数据分析中的重要性。然后，介绍了如何在Origin中通过视图操作、菜单命令和脚本自动化实现矩阵转置。此外，本文还探讨了矩阵转置与其他矩阵操作如乘法、逆矩阵的关联性。在实验数据处理方面，本文分析了转置矩阵在数据导入、预处理、多变量分析及统计分析中的应用。最后，通过案例分析，展示了转置矩阵在化学、生物和物理实验数据分析中的具体应用，进一步加深了对Origin中矩阵转置操作的理解和运用。

# 关键字
Origin软件；矩阵转置；数据分析；脚本自动化；数据预处理；案例分析

参考资源链接：[Origin入门：详细教程——矩阵转置与工作环境设置](https://wenku.csdn.net/doc/5mxv9nf4ba?spm=1055.2635.3001.10343)
# 1. Origin软件及其矩阵操作基础

Origin软件是一款集数据处理、统计分析和图形绘制于一体的科研软件，它广泛应用于工程、物理、生物、医学等多个领域。矩阵操作是Origin中的重要功能，尤其在复杂数据处理和分析中具有独特的作用。

Origin中的矩阵操作提供了丰富的功能，包括矩阵的基本运算，矩阵函数运算，矩阵的转置、求逆等。其中，矩阵转置是进行数据分析的一个重要手段，它可以通过改变矩阵元素的行列位置，重新组织数据，从而达到简化问题、发现数据间关系的目的。

Origin软件在处理矩阵数据时，提供了一种独特的矩阵视图方式，这使得用户可以直观地查看和编辑矩阵数据。在Origin中，我们可以通过菜单命令，或者编写脚本的方式来实现矩阵的转置操作，极大地方便了用户的操作。

# 2. 矩阵转置的理论基础与应用

矩阵转置是线性代数中一个基础且重要的概念，它在数据分析、数学运算以及工程计算等领域有着广泛的应用。在这一章节中，我们将深入探讨矩阵转置的定义、数学原理及其在数据分析中的重要性，并通过Origin软件这一平台，阐述如何高效地实现矩阵转置及其与其他矩阵操作的关联。

### 矩阵和转置的概念

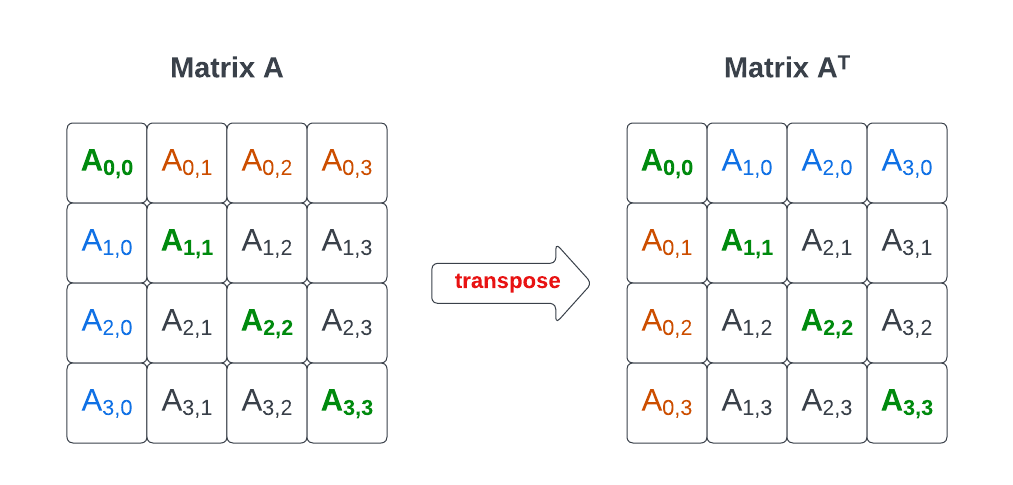
矩阵是由数字、符号或表达式按一定规则排列成的矩形阵列。在数学中，矩阵是表示和处理线性关系的一种重要方式。矩阵的转置是将矩阵的行变成列、列变成行的操作，用符号`A^T`表示原矩阵`A`的转置。转置操作是可逆的，即`(A^T)^T = A`。对于一个`m×n`的矩阵，其转置将是一个`n×m`的矩阵。

#### 矩阵转置的数学原理

从线性代数的角度来看，矩阵转置是线性空间内一个特殊的线性变换，它反映了向量空间中基向量的对换。在进行矩阵乘法操作时，转置操作常常会与之相伴，以确保矩阵的维数匹配。例如，假设有两个矩阵`A(m×n)`和`B(n×p)`，则它们的乘积`C = AB`是一个`m×p`的矩阵。当需要进一步计算`C`与另一个矩阵的乘积时，可能需要对`C`进行转置。

#### 矩阵转置在数据分析中的重要性

在数据分析中，矩阵转置是一个基础操作，常用于数据结构的转换。例如，在进行多变量统计分析时，可能需要将数据矩阵从宽格式转换为长格式，或反之。此外，在矩阵乘法中，转置操作可以改变矩阵的行与列，从而使得矩阵乘法可以顺利进行。特别是在处理大型矩阵时，转置操作可以将存储和计算的瓶颈从CPU转移到内存，从而提高计算效率。

### Origin中矩阵转置的实现步骤

Origin是一款广泛应用于科学绘图和数据分析的软件，其矩阵视图提供了丰富的矩阵操作功能。下面我们将介绍通过Origin实现矩阵转置的不同方法，包括菜单命令和脚本自动化等。

#### Origin矩阵视图的操作基础

在Origin中操作矩阵之前，首先需要了解其矩阵视图的基本概念。Origin的矩阵视图可以理解为Excel的二维表格，其中包含数值型的数据，但Origin的矩阵视图可以更有效地处理矩阵运算。

- 在Origin中打开矩阵窗口，可以通过菜单栏选择`Matrix` -> `New`，然后选择矩阵的行列数，来创建一个新的矩阵。
- 也可以通过导入外部数据文件（如CSV，MAT等格式）来创建矩阵。

#### 通过菜单命令实现矩阵转置

Origin提供了直观的菜单命令来实现矩阵转置，具体步骤如下：

1. 打开矩阵窗口，并确保矩阵窗口处于激活状态。
2. 点击菜单栏中的`Matrix` -> `Matrix Operation` -> `Transpose`。此时Origin会自动将选中的矩阵进行转置操作，并弹出一个新的矩阵窗口来显示转置后的矩阵。

#### 使用Origin脚本自动化矩阵转置

Origin脚本是实现复杂矩阵操作自动化的有效手段。Origin提供的LabTalk脚本语言可以执行包括矩阵转置在内的多种操作。

// 创建一个脚本文件，执行以下命令进行矩阵转置
win -o myMatrix; // 打开名为myMatrix的矩阵窗口
matrix -o myMatrix; // 使用矩阵操作命令
matrix transpose:=1; // 设置矩阵转置参数为1（即进行转置）

在脚本中，`transpose`参数设置为1表示执行转置，为0则不进行转置操作。

### 矩阵转置与其他矩阵操作的关联

矩阵转置在矩阵运算中扮演着桥梁的角色，它与其他矩阵操作有着密切的关联，特别是在矩阵乘法和矩阵求逆等操作中。

#### 矩阵乘法和转置的关系

在矩阵乘法中，根据分配律和结合律，转置操作可以简化某些计算步骤，尤其是在处理大规模矩阵乘法时。例如，如果`A(m×n)`，`B(n×p)`，则`(AB)^T = B^T A^T`。这意味着转置操作允许我们首先计算`B^T`和`A^T`的乘积，有时这样做会更加高效。

#### 转置与逆矩阵的关系

对于一个方阵`A`，如果它可逆，则其逆矩阵记为`A^-1`。若`A`进行转置得到`A^T`，那么如果`A`可逆，`A^T`也可逆，且`(A^-1)^T = (A^T)^-1`。这一性质在处理矩阵方程和进行数学推导时非常有用。

通过Origin软件，我们不仅可以实现基本的矩阵操作，还可以借助其强大的脚本功能实现自动化和优化处理。在下一章节中，我们将探讨如何在实验数据处理中应用转置矩阵，以及如何构建和组织实验数据以适应矩阵操作的需要。

# 3. 转置矩阵在实验数据处理