深度学习正则化实战：应用技巧与案例研究

# 1. 深度学习正则化基础

在构建和优化深度学习模型的过程中，正则化技术扮演着至关重要的角色。正则化不仅仅是防止模型过拟合的一个手段，更是提升模型泛化能力、处理不确定性以及增强模型在现实世界数据上的表现的关键策略。本章将深入探讨正则化的根本概念、理论基础以及在深度学习中的重要性，为后续章节中对各类正则化技术的分析和应用打下坚实的基础。

# 2. 正则化技术的理论与实践

正则化技术是深度学习领域中防止过拟合、提升模型泛化能力的关键策略。在这一章节中，我们将深入了解正则化在深度学习中的作用、探索常见的正则化方法，并分析正则化参数的调优策略。

## 2.1 正则化在深度学习中的作用

### 2.1.1 防止过拟合

过拟合是指模型对训练数据拟合得太好，以至于泛化到未知数据的能力下降的现象。深度学习模型的参数众多，容易在训练集上学习到过于复杂的关系，导致过拟合。正则化通过向损失函数中添加一个额外的惩罚项来抑制模型复杂度，迫使模型学习更加平滑和简洁的特征。

例如，L2正则化项在损失函数中添加了一个权重的平方和，权重较大时惩罚项值显著增加，从而驱动权重整体变小，减少模型复杂度。代码示例：

# L2正则化项添加至损失函数中
def l2_regularized_loss(weights, regularization_strength):
    loss = compute_loss(weights)  # 假设这是计算损失的函数
    l2_penalty = regularization_strength * sum(w ** 2 for w in weights)
    return loss + l2_penalty

# 假设的权重列表
weights = [1.0, -2.0, 3.0, -4.0]
# 正则化系数
regularization_strength = 0.1

# 计算带有L2正则化的损失值
loss_with_regularization = l2_regularized_loss(weights, regularization_strength)
print(f"Loss with L2 regularization: {loss_with_regularization}")

### 2.1.2 提升模型泛化能力

正则化技术的核心目的是提高模型在未知数据上的表现，即泛化能力。通过减小模型复杂度，正则化促使模型学习更加通用的特征，这些特征能够在新的数据集上产生更好的性能。

在实际应用中，通过交叉验证等技术，选择合适的正则化参数能够显著提升模型的泛化性能。下面的表格展示了几种常见的正则化方法及其优缺点：

| 正则化方法 | 优点 | 缺点 |
| --- | --- | --- |
| L1正则化 | 产生稀疏权重，有助于特征选择 | 可能导致模型不稳定 |
| L2正则化 | 防止过拟合，保持模型稳定性 | 对异常值敏感 |
| Dropout | 提升模型鲁棒性，易于实现 | 可能需要调整更多的超参数 |
| 数据增强 | 增加模型对数据变化的鲁棒性 | 计算成本高，可能引入噪声 |

## 2.2 常见正则化方法

### 2.2.1 L1和L2正则化

L1正则化和L2正则化是两种经典的正则化方法，它们通过不同的方式对模型复杂度进行控制。L1正则化倾向于生成稀疏模型，有助于特征选择；而L2正则化则使模型权重更加平滑，对于防止过拟合尤其有效。

在实际应用中，选择L1还是L2正则化取决于具体问题和模型的需求。代码示例展示了L1和L2正则化在优化问题中的体现：

import numpy as np

def l1_regularized_gradient_descent(X, y, learning_rate, regularization_strength):
    weights = np.zeros(X.shape[1])
    for _ in range(iterations):
        # 假设这里计算了梯度
        gradient = compute_gradient(X, y, weights)
        # 添加L1正则化项
        gradient += regularization_strength * np.sign(weights)
        weights -= learning_rate * gradient
    return weights

def l2_regularized_gradient_descent(X, y, learning_rate, regularization_strength):
    weights = np.zeros(X.shape[1])
    for _ in range(iterations):
        # 假设这里计算了梯度
        gradient = compute_gradient(X, y, weights)
        # 添加L2正则化项
        gradient += regularization_strength * 2 * weights
        weights -= learning_rate * gradient
    return weights

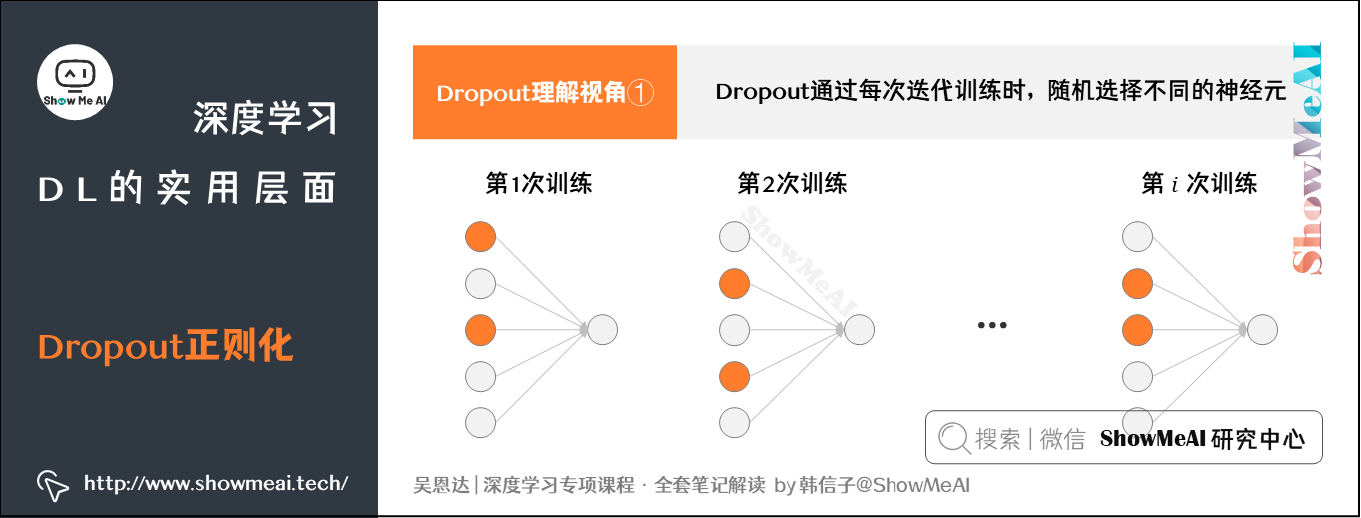
### 2.2.2 Dropout技术

Dropout是一种在训练期间随机丢弃网络中部分神经元的正则化技术，其目的是减少神经元间的共适应性，迫使网络学习更加鲁棒的特征表示。

在深度学习框架中，如TensorFlow或PyTorch，Dropout可以简单地通过在神经网络模型中加入Dropout层来实现。下面是一个简单的例子：

from keras.layers import Dropout
from keras.models import Sequential

# 假设input_shape是模型输入层的形状
model = Sequential()
model.add(Dense(64, activation='relu', input_shape=input_shape))
# 添加Dropout层，rate参数表示丢弃的比例
model.add(Dropout(0.5))
model.add(Dense(10, activation='softmax'))

### 2.2.3 数据增强

数据增强是通过对训练数据进行一系列变换来人为增加数据多样性的方法，常用的变换包括旋转、缩放、平移和颜色变换等。在图像识别任务中，数据增强是一种非常有效的正则化手段。

数据增强的实现依赖于数据集的特性，下面是一个简单的图像数据增强流程，使用了Python的imgaug库：

import imgaug.augmenters as iaa

# 定义一个增强序列，包括旋转和缩放
seq = iaa.Sequential([
    iaa.Affine(rotate=(-10, 10)),  # 旋转
    iaa.Affine(scale={'x': (0.8, 1.2), 'y': (0.8, 1.2)})  # 缩放
])

# 假设images是一个包含图像数据的NumPy数组
augmented_images = seq.augment_images(images)

## 2.3 正则化参数调优

### 2.3.1 超参数的重要性

在正则化方法中，例如L1和L2正则化的强度，或者Dropout层中神经元被丢弃的概率，这些参数被统称为超参数。超参数的选择对模型的性能有着决定性的影响。

超参数的调整是一个迭代的过程，通常需要使用如网格搜索、随机搜索或贝叶斯优化等方法来系统地寻找最优值。下面是使用网格搜索进行超参数优化的基本流程：

from sklearn.model_selection import GridSearchCV

# 假设estimator是我们的模型，param_grid是我们希望搜索的参数网格
grid_search = GridSearchCV(estimator, param_grid, cv=5)
grid_search.fit(X_train, y_train)

# 最佳参数及最佳分数
best_params = grid_search.best_params_
best_score = grid_search.best_score_

### 2.3.2 调优策略与方法

正则化参数的调优策略包括但不限于网格搜索、随机搜索、贝叶斯优化等。在实际操作中，根据问题的复杂性、数据的规模和模型的类型，选择合适的调优方法至关重要。

贝叶斯优化是一种考虑先验信息和已评估点的性能，来指导搜索最优超参数的方法。它通常能够更高效地在参数空间中找到较优的配置。以下是使用贝叶斯优化的一个代码示例：

from skopt im