多目标优化问题的挑战与NSGA-II的解决方案：解决策略全解析


# 摘要
多目标优化是决策科学中的一个关键领域，其目的是在多个相互冲突的目标之间找到最佳平衡。NSGA-II算法因其在处理这类问题时的高效性和有效性而受到广泛关注。本文首先介绍了多目标优化的基础知识以及NSGA-II算法的理论框架，包括目标冲突、偏好排序以及Pareto优化理论。随后，详细探讨了NSGA-II的关键技术与实施步骤，如快速非支配排序、密度估计与拥挤距离，以及算法参数的敏感性分析和调优策略。此外，本文还涉及NSGA-II的并行化策略和改进版本，以及该算法在工程设计、路径规划和调度问题中的实际应用实例。最后，本文总结了NSGA-II当前面临的挑战、未来研究方向和从理论到实践转化的潜力。

# 关键字
多目标优化；NSGA-II算法；Pareto优化；快速非支配排序；并行化策略；工程应用实例

参考资源链接：[NSGA-II算法详解：多目标优化与Pareto最优解](https://wenku.csdn.net/doc/87dsdawwwu?spm=1055.2635.3001.10343)
# 1. 多目标优化问题的基础知识

在这一章节中，我们将探讨多目标优化问题的核心概念和基本原理。首先，我们将定义何为多目标优化问题，并解释目标冲突与权衡的本质。这将引导我们理解为什么在存在相互冲突目标的场景下，单一解决方案往往无法满足所有条件，因此需要在不同目标之间进行选择和折衷。

接下来，我们将深入了解偏好和解的排序，这是理解和解决多目标问题的关键。我们将讨论如何通过定义偏好来对潜在解决方案进行排序，并探索这些排序如何帮助我们识别最优解集。通过这些讨论，读者将对多目标优化问题有一个全面而深入的理解，为后续章节深入探讨NSGA-II算法以及其关键技术和应用案例打下坚实的基础。

## 1.1 目标的冲突与权衡

在真实世界的决策过程中，往往面临着多个目标之间的权衡。例如，开发一个产品时，我们可能需要在成本、功能和上市时间之间做出选择。这些目标之间可能存在冲突，比如增加功能可能会导致成本上升或上市时间推迟。多目标优化问题正是要寻找满足所有这些目标的最佳解决方案。

## 1.2 偏好和解的排序

偏好定义了决策者对于不同目标的重要性和优先级。一个解（解决方案）的排序依赖于其如何满足这些偏好。排序过程会根据决策者设定的权重和目标之间的相对重要性，对一组潜在解进行排序。理解偏好对于在众多可行解中筛选出最优解集至关重要。

## 1.3 本章小结

本章为理解多目标优化问题奠定了基础。我们讨论了目标冲突的本质以及偏好设置在解排序中的作用。在下一章，我们将深入探讨NSGA-II算法，这是一个有效的多目标优化算法，它利用特定的排序机制和选择策略来找到一组高质量的Pareto最优解。

# 2. NSGA-II算法的理论框架

### 2.1 多目标优化的基本概念

在研究多目标优化问题时，我们首先需要掌握一些基础概念。多目标优化问题与单目标优化问题不同的是，它同时涉及到多个需要优化的目标函数，并且这些目标之间往往存在冲突，即一个目标的改善可能会影响其他目标的效果。

#### 2.1.1 目标的冲突与权衡

在多目标优化中，目标之间的冲突意味着我们不可能同时达到所有目标的最优解。这就要求我们必须在不同目标之间做出权衡。例如，在设计一辆汽车时，我们可能需要在车辆的速度和油耗之间做出选择：追求高速度可能会导致更高的油耗。这种权衡在多目标优化中至关重要，需要通过优化算法来找到一个折中的解决方案。

#### 2.1.2 偏好和解的排序

在实际的多目标优化问题中，决策者通常对不同的目标有不同的偏好。这些偏好可以通过为不同目标赋予不同的权重来体现，或者通过其他方法如目标规划来综合考虑。解的排序是指对所有可能的解进行比较，根据决策者的偏好以及各个目标的优化程度来排序，找出最优解集。

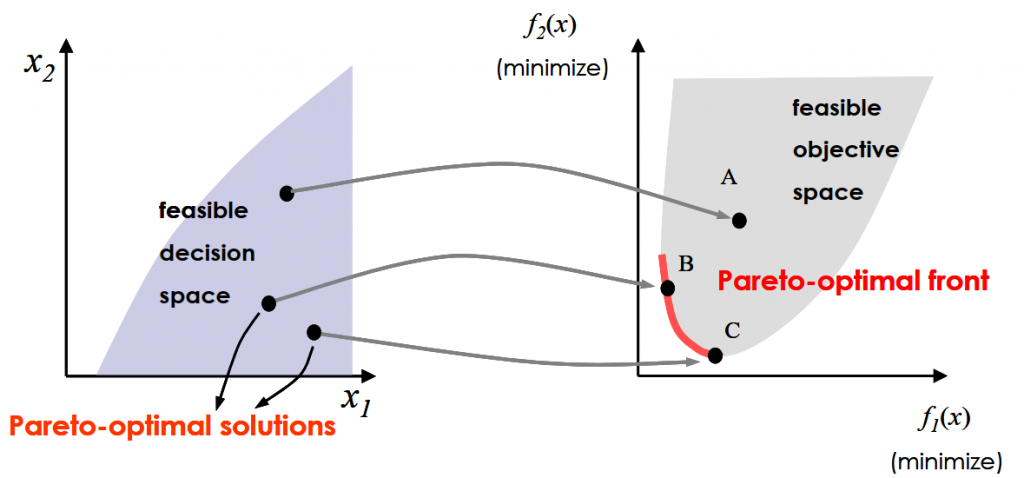
### 2.2 Pareto优化理论

Pareto优化理论是多目标优化领域的基石，它的核心思想是通过找到一组解，其中任何一个解的改进都会导致至少一个其他解变差。

#### 2.2.1 Pareto支配关系

Pareto支配关系是定义在一组解上的一个二元关系。一个解被定义为支配另一个解，如果它在所有目标上都不弱于另一个解，并且至少在一个目标上比另一个解更好。换句话说，如果一个解不能在所有目标上同时被另一个解所支配，则该解被认为是Pareto最优的。

#### 2.2.2 Pareto前沿和Pareto最优解集

Pareto前沿是指所有Pareto最优解的集合，它代表了问题的最优解的边界。Pareto最优解集包含了所有可能的最优权衡解，为决策者提供了选择的余地。在实际应用中，决策者可以根据自己的偏好从Pareto前沿中选择最终的解决方案。

### 2.3 NSGA-II算法概述

NSGA-II算法，即非支配排序遗传算法II（Non-dominated Sorting Genetic Algorithm II），是一种流行的多目标优化算法。它通过模拟自然选择过程来寻找问题的Pareto最优解。

#### 2.3.1 算法的起源和动机

NSGA-II是在其前身NSGA的基础上发展起来的。NSGA在解决多目标优化问题时表现出色，但其高计算复杂度限制了其应用范围。NSGA-II通过引入快速非支配排序和拥挤距离的概念，显著降低了计算复杂度，同时提高了算法的性能，尤其是在解决大规模问题时表现更为突出。

#### 2.3.2 算法的组成和流程

NSGA-II主要由三个关键部分组成：初始化种群、快速非支配排序、以及选择、交叉和变异操作。算法流程如下：

1. 初始化一个随机种群。
2. 进行快速非支配排序，确定种群中各个个体的支配等级。
3. 使用拥挤距离来保持种群的多样性。
4. 通过选择、交叉和变异操作生成新的种群。
5. 重复步骤2-4，直到满足终止条件（如达到预定的迭代次数或解的质量不再提高）。

NSGA-II的核心思想在于通过迭代过程逐步逼近问题的Pareto最优解集。在接下来的章节中，我们将深入探讨NSGA-II的关键技术与实施步骤。

# 3. NSGA-II的关键技术与实施步骤

## 3.1 快速非支配排序

### 3.1.1 排序过程详解

快速非支配排序是NSGA-II算法的核心，它旨在将种群中的个体划分成不同的等级或层级，每个层级代表了个体在Pareto支配关系中的位置。第一等级包含那些没有被任何其他个体支配的个体，这些个体被认为是当前种群中的最佳解。随后的等级包含的是那些被较少个体支配的个体，以此类推，直到最后所有的个体都被排序完毕。

非支配排序的执行流程如下：
1. **初始化**：对于种群中的每一个个体，计算其支配计数（即被多少其他个体支配）和支配集（支配该个体的所有个体集合）。
2. **选择第一等级**：找出支配计数为零的个体，这些个体构成第一等级。
3. **移除已排序个体**：从种群中移除所有第一等级的个体，并更新剩余个体的支配计数和支配集。
4. **递归排序**：重复上述过程，直到所有个体被排序到不同的等级。

以下是第一等级个体选择的伪代码：