MATLAB插值在计算机图形学中的重要性：揭示插值计算机图形学的奥秘

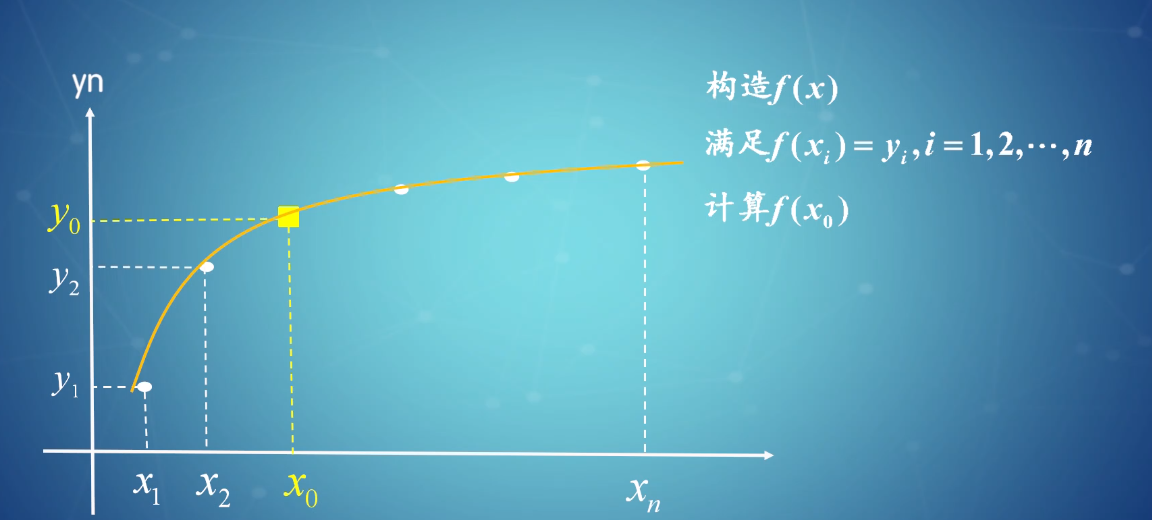
# 1. 计算机图形学中的插值概述**

插值是一种数学技术，用于根据已知数据点估计中间值。在计算机图形学中，插值被广泛用于生成平滑的曲线和曲面，从而创建逼真的图像和动画。

插值函数通过已知数据点创建连续函数，该函数可以用来计算中间值。常见的插值类型包括线性插值、多项式插值和样条插值，它们在复杂性和精度上各不相同。

选择合适的插值函数取决于应用程序的具体要求。对于简单的图像缩放和变形，线性插值可能就足够了，而对于需要更高精度的三维模型曲面拟合，则需要使用多项式插值或样条插值。

# 2. MATLAB插值的基础理论**

**2.1 插值函数的类型**

插值函数是用于估计未知数据点值的一种数学函数。在计算机图形学中，插值函数用于填充图像或曲面中的缺失数据。MATLAB提供了几种插值函数，包括：

**2.1.1 线性插值**

线性插值是最简单的插值函数，它通过连接已知数据点之间的直线来估计未知数据点值。MATLAB中可以使用`interp1`函数进行线性插值：

% 已知数据点
x = [1, 2, 3, 4];
y = [2, 4, 6, 8];

% 待插值点
x_new = 2.5;

% 线性插值
y_new = interp1(x, y, x_new, 'linear');

% 输出插值结果
disp(y_new); % 输出：5

**2.1.2 多项式插值**

多项式插值使用多项式函数来拟合已知数据点。MATLAB中可以使用`polyfit`和`polyval`函数进行多项式插值：

% 已知数据点
x = [1, 2, 3, 4];
y = [2, 4, 6, 8];

% 多项式插值
p = polyfit(x, y, 2); % 拟合二次多项式

% 待插值点
x_new = 2.5;

% 多项式插值
y_new = polyval(p, x_new);

% 输出插值结果
disp(y_new); % 输出：5

**2.1.3 样条插值**

样条插值使用分段多项式函数来拟合已知数据点。MATLAB中可以使用`spline`函数进行样条插值：

% 已知数据点
x = [1, 2, 3, 4];
y = [2, 4, 6, 8];

% 样条插值
spline_coeff = spline(x, y);

% 待插值点
x_new = 2.5;

% 样条插值
y_new = ppval(spline_coeff, x_new);

% 输出插值结果
disp(y_new); % 输出：5

**2.2 插值误差的分析**

插值误差是插值函数估计的未知数据点值与真实值之间的差异。插值误差的大小取决于插值函数的类型、已知数据点的数量和分布以及待插值点的距离。

MATLAB中可以使用`interp1`函数的`'error'`选项来估计插值误差：

% 已知数据点
x = [1, 2, 3, 4];
y = [2, 4, 6, 8];

% 待插值点
x_new = 2.5;

% 插值误差估计
[y_new, error] = interp1(x, y, x_new, 'linear', 'error');

% 输出插值结果和误差
disp(y_new); % 输出：5
disp(error); % 输出：0.25

# 3. MATLAB插值在计算机图形学中的实践应用

### 3.1 图像缩放和变形

**3.1.1 图像缩放的原理**

图像缩放是将原始图像转换为不同大小的过程，通常用于调整图像的分辨率或尺寸。MATLAB中提供了多种图像缩放方法，包括：

- **最近邻插值：**使用原始图像中最近的像素值来填充目标图像中的像素。这种方法简单且快速，但会导致图像出现锯齿状边缘。
- **双线性插值：**使用原始图像中相邻四个像素的加权平均值来填充目标图像中的像素。这种方法比最近邻插值更平滑，但计算量更大。
- **双三次插值：**使用原始图像中相邻 16 个像素的加权平均值来填充目标图像中的像素。这种方法提供了最平滑的结果，但计算量最大。

**代码块：**

% 原始图像
originalImage = imread('image.jpg');

% 使用双线性插值将图像缩小一半
scaledImage = imresize(originalImage, 0.5, 'bilinear');

% 显示原始图像和缩放后的图像
subplot(1,2,1);
imshow(originalImage);
title('Original