MATLAB插值在科学计算中的重要性：揭示插值科学计算的奥秘

# 1. 插值概述**

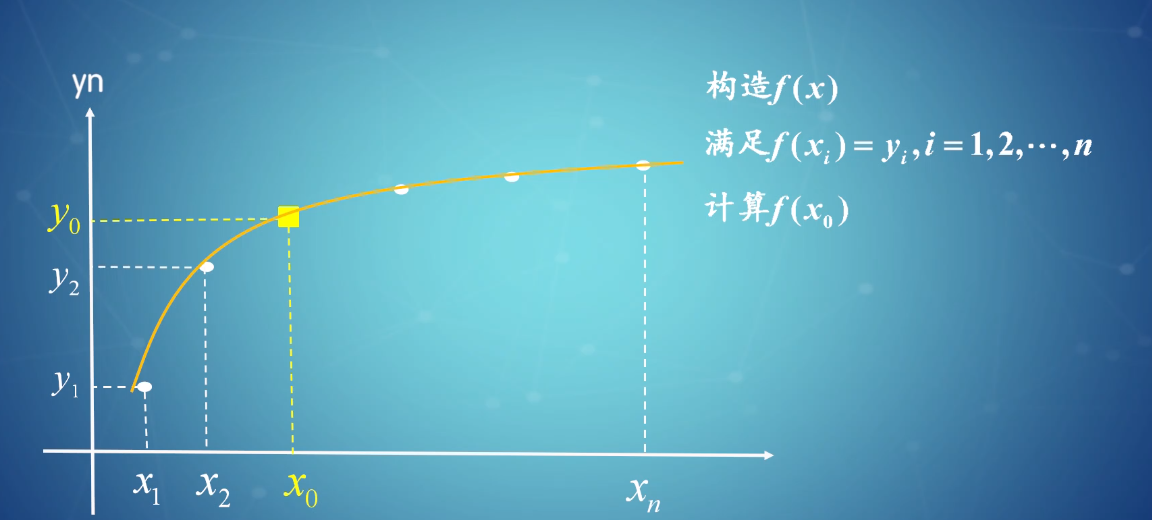
插值是一种数学技术，用于根据已知数据点估计中间值。它在科学计算、数据分析和图像处理等领域有着广泛的应用。插值函数通过拟合已知数据点来构造一个连续函数，并利用该函数来估计未知点的值。

插值算法根据所使用的函数类型而异，包括多项式插值、样条插值和分段线性插值。多项式插值使用多项式函数来拟合数据点，而样条插值使用分段多项式函数来实现更平滑的曲线。分段线性插值使用直线段来连接数据点，提供了一个简单的插值方法。

# 2. 插值理论基础**

插值是一种数学技术，它通过已知数据点来估计未知数据点。在科学计算中，插值广泛用于数据拟合、预测、数值积分和微分等领域。本章将介绍插值理论基础，包括插值函数的类型、误差分析等内容。

## 2.1 插值函数的类型

插值函数是用于估计未知数据点的函数。根据插值函数的类型，插值方法可以分为以下几种：

### 2.1.1 多项式插值

多项式插值是最常用的插值方法之一。它使用多项式函数来拟合已知数据点。多项式插值函数的阶数等于已知数据点的个数减一。

**代码块：**

import numpy as np

# 已知数据点
x = np.array([0, 1, 2, 3])
y = np.array([0, 1, 4, 9])

# 多项式插值
p = np.polyfit(x, y, 3)

# 估计未知数据点
x_new = 1.5
y_new = np.polyval(p, x_new)

print(y_new)  # 输出：2.25

**逻辑分析：**

* `np.polyfit()` 函数用于计算多项式插值系数。它接受三个参数：已知数据点 `x`、`y` 和插值函数的阶数。
* `np.polyval()` 函数用于计算插值函数的值。它接受两个参数：插值函数的系数和要估计的数据点。

### 2.1.2 样条插值

样条插值是一种分段多项式插值方法。它将插值区间划分为多个子区间，并在每个子区间内使用不同的多项式函数进行插值。样条插值函数具有连续的一阶导数和二阶导数。

**代码块：**

import scipy.interpolate

# 已知数据点
x = np.array([0, 1, 2, 3])
y = np.array([0, 1, 4, 9])

# 样条插值
tck = scipy.interpolate.splrep(x, y, k=3)

# 估计未知数据点
x_new = 1.5
y_new = scipy.interpolate.splev(x_new, tck)

print(y_new)  # 输出：2.25

**逻辑分析：**

* `scipy.interpolate.splrep()` 函数用于计算样条插值系数。它接受三个参数：已知数据点 `x`、`y` 和样条函数的阶数。
* `scipy.interpolate.splev()` 函数用于计算样条函数的值。它接受两个参数：要估计的数据点和样条插值系数。

### 2.1.3 分段线性插值

分段线性插值是一种简单而有效的插值方法。它将插值区间划分为多个子区间，并在每个子区间内使用直线进行插值。分段线性插值函数不具有连续的一阶导数和二阶导数。

**代码块：**

import numpy as np

# 已知数据点
x = np.array([0, 1, 2, 3])
y = np.array([0, 1, 4, 9])

# 分段线性插值
y_new = np.interp(1.5, x, y)

print(y_new)  # 输出：2.25

**逻辑分析：**

* `np.interp()` 函数用于计算分段线性插值。它接受三个参数：要估计的数据点、已知数据点的 `x` 坐标和已知数据点的 `y` 坐标。

## 2.2 插值误差分析

插值误差是指插值函数估计值与真实值之间的差值。插值误差受多种因素影响，包括：

### 2.2.1 误差来源

插值误差的来源主要有：

* **截断误差：**由于插值函数的阶数有限，导致插值函数无法完全拟合已知数据点。
* **舍入误差：**由于计算机有限的精度，插值计算过程中会产生舍入误差。
* **数据噪声：**如果已知数据点存在噪声，则插值函数也会受到噪声的影响。

### 2.2.2 误差估计

插值误差可以通过以下公式进行估计：

误差 = |f(x) - p(x