【R语言MCMC探索性数据分析】：方法论与实例研究，贝叶斯统计新工具

# 1. MCMC方法论基础与R语言概述

## 1.1 MCMC方法论简介
**MCMC (Markov Chain Monte Carlo)** 方法是一种基于马尔可夫链的随机模拟技术，用于复杂概率模型的数值计算，特别适用于后验分布的采样。MCMC通过构建一个马尔可夫链，使得其平稳分布为目标后验分布，通过链的遍历来获取样本，进而进行统计推断。

## 1.2 R语言在统计分析中的地位
R语言是一种用于统计计算和图形表示的编程语言和环境。它因其强大的统计分析能力和开放的社区支持，成为数据科学家和统计学者的首选。R语言提供了丰富的包来支持从基本的统计测试到高级的机器学习算法。

## 1.3 MCMC与R语言的结合
将MCMC方法与R语言结合起来，可以构建强大的统计模型并进行精确的推断分析。R的贝叶斯统计包如 `rstan`、`MCMCpack` 等，为MCMC算法的实现和应用提供了便利。本章将介绍MCMC的基本原理、R语言的安装和使用，以及二者结合的重要性和实践方法。

通过本章的学习，读者将对MCMC方法有初步认识，并掌握在R语言环境中实现MCMC算法的基础知识，为深入学习后续章节奠定坚实基础。

# 2. R语言中的贝叶斯统计基础

### 2.1 贝叶斯统计原理

#### 2.1.1 概率与先验分布

在贝叶斯统计中，概率不仅仅是一个频率的概念，它还是对不确定性的量化表达。这与经典的频率论概率观形成对比，后者认为概率是长期频率的稳定值。在贝叶斯框架中，概率是度量个人信念的强度的一种方法。先验分布，即在观测数据之前对参数的个人信念，是贝叶斯方法论的核心组成部分。

先验分布的引入使得我们可以将先前的知识或信念纳入到分析中。它是对参数可能取值的一个概率分布，代表了在观察到数据之前我们对参数状态的了解。例如，在抛硬币实验中，如果没有任何先前信息，我们可以使用均匀分布作为先验，表示硬币正面朝上的概率是0.5。如果有先前信息表明硬币可能不平衡，我们可以使用更偏向一边的先验分布。

在R语言中，我们可以使用专门的函数或分布来表示先验，例如`dbeta()`函数可用于创建贝塔分布，它是一个常用的先验分布形式，特别是在二项分布参数的贝叶斯分析中。

#### 2.1.2 后验分布的理解和计算

后验分布是在考虑了先验分布和新数据之后，对参数的更新后的信念。它是贝叶斯统计中的核心输出，反映了在观测到数据之后对参数的认识。后验分布的计算遵循贝叶斯定理：

\[ P(\theta | X) = \frac{P(X | \theta) P(\theta)}{P(X)} \]

其中，\( P(\theta | X) \) 是后验分布，\( P(X | \theta) \) 是似然函数，\( P(\theta) \) 是先验分布，而 \( P(X) \) 是边缘似然，用于归一化计算。

在实际应用中，后验分布的计算往往较为复杂，可能涉及高维积分或者复杂的模拟过程。然而，借助R语言和相应的统计包，我们可以有效地计算后验分布，并且可以进一步分析这些分布来估计参数值、预测未来数据或者进行假设检验。

在R中，`rstan`包是一个常用的工具来通过基于哈密尔顿蒙特卡洛方法的Stan语言进行后验推断。我们可以使用`stan()`函数来抽取后验样本，并进一步对这些样本进行分析以得到参数估计的统计特性。

### 2.2 R语言的贝叶斯统计包

#### 2.2.1 介绍常用的贝叶斯统计包

R语言提供了丰富的贝叶斯统计包，使得在实践中应用贝叶斯方法变得更为简便和高效。一些流行的包包括`rstanarm`、`brms`和`MCMCpack`。这些包为不同类型的数据分析提供了广泛的功能，涵盖了线性回归、广义线性模型、多层次模型等。

- `rstanarm`：基于Stan的语言，允许用户以类似`lm()`和`glm()`的语法来拟合贝叶斯模型。
- `brms`：一个灵活的R包，可以拟合全贝叶斯广义线性模型和多层次模型。
- `MCMCpack`：提供一系列用于Markov Chain Monte Carlo算法的函数，用于模拟各种统计模型。

这些包极大地降低了实现贝叶斯分析的门槛，使得没有深厚贝叶斯理论和编程背景的用户也能够使用贝叶斯方法。

#### 2.2.2 包的安装和基础使用方法

安装这些包非常简单，通常只需要使用R的包管理工具`install.packages()`函数。例如，安装`rstanarm`包的命令是：

install.packages("rstanarm")

安装之后，我们可以使用`library()`函数加载包：

library(rstanarm)

基础使用方法涉及到如何使用包内的函数来定义模型、拟合模型以及生成后验预测。例如，使用`rstanarm`包进行线性回归的代码如下：

# 使用rstanarm包进行线性回归
stan_glm(y ~ x, family = gaussian(), data = my_data)

这里的`stan_glm()`函数是`rstanarm`包中用于拟合广义线性模型的函数。`y ~ x`定义了模型公式，`family = gaussian()`指定了因变量的分布，`data = my_data`指定了数据集。拟合模型后，我们可以进一步利用输出的结果进行诊断、预测和参数估计。

### 2.3 MCMC在贝叶斯框架中的角色

#### 2.3.1 MCMC算法简介

MCMC算法是一类利用马尔可夫链的特性来进行采样，从而估计复杂概率分布的数值方法。贝叶斯框架下参数的后验分布往往是高维且复杂的，直接进行数学上的积分计算非常困难，甚至是不可能的。MCMC算法则能够有效地在后验分布上进行采样，从而获取后验分布的特征信息。

MCMC算法包括许多类型，比如吉布斯采样、Metropolis-Hastings算法、哈密尔顿蒙特卡洛等。每种算法有其独特的采样策略和适用场景。

在R语言中，我们可以利用多个包来实现MCMC算法。如`MCMCpack`提供了一系列实现不同MCMC方法的函数，`rstan`包提供了基于Stan语言的高效MCMC算法。

#### 2.3.2 MCMC与贝叶斯推断的关系

MCMC算法与贝叶斯推断的结合为复杂统计问题的解决提供了强大的工具。在贝叶斯框架下，一旦确定了先验分布和似然函数，我们就可以利用MCMC算法来获得后验分布的样本。这些样本不仅能够给出参数的点估计（比如后验均值、中位数），还可以给出关于参数不确定性的完整描述（比如后验分布的方差、可信区间）。

在实际操作中，`rstan`包的`stan()`函数就是通过哈密尔顿蒙特卡洛算法来实现这一过程的，它不仅可以处理简单的模型，还能够应对包含多种分布和复杂结构的模型。

下一章节将深入探讨MCMC算法的理论基础及其在R语言中的实现方式，包括MCMC算法的调优以及收敛性检验等关键概念。

# 3. MCMC算法与R语言实现

在理解了贝叶斯统计和MCMC方法论的基础之后，我们将深入了解如何在R语言中实现MCMC算法。这一章节将带领读者从理论上掌握马尔可夫链的性质和随机游走的基本概念，并实际操作如何在R语言中进行MCMC采样、诊断和收敛性检验。进一步，我们将探讨如何通过调优MCMC参数以提高算法效率，以及处理高维问题的技术。

## 3.1 MCMC算法的理论基础

### 3.1.1 马尔可夫链的性质

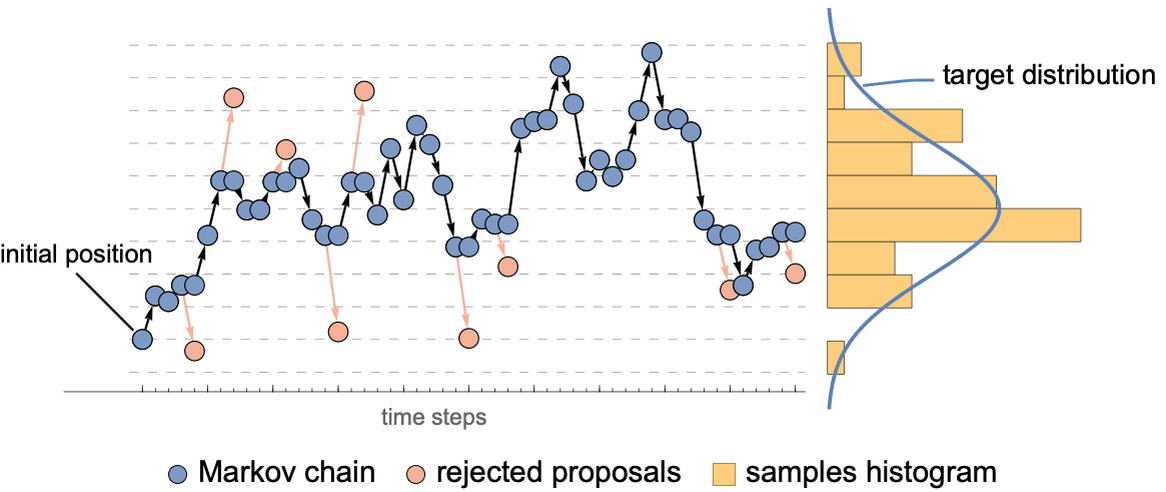
马尔可夫链是一个随机过程，其未来状态仅依赖于当前状态，而不依赖于如何到达当前状态。这意味着，如果系统当前处于状态X，那么它下一步转移到状态Y的概率只与X有关，与之前的状态历史无关。这种“无记忆性”是马尔可夫链的核心特性。

理解马尔可夫链对于MCMC算法来说至关重要。MCMC算法利用了马尔可夫链的性质，通过设计满足特定条件的转移概率，来确保马尔可夫链在经过足够长时间的迭代后，其状态分布能够近似目标分布。

### 3.1.2 随机游走和平稳分布

随机游走是马尔可夫链的一种特例，它代表了一个在状态空间中随机移动的序列。在MCMC中，随机游走通常用来描述潜在参数空间中的探索过程。这个过程是随机的，并且通过精心设计的转移概率，可以在目标分布上进行采样。

对于MCMC算法而言，一个非常重要的概念是平稳分布。平稳分布是指，当马尔可夫链足够长时间地运行后，其状态分布会收敛到一个固定不变的分布，这个分布就被称为平稳分布。如果一个马尔可夫链的平稳分布恰好是我们想要采样的目标分布，那么这个马尔可夫链就是可用的。

graph LR
    A[起始状态] --> B{转移概率}
    B -->|p| C[状态1]
    B -->|1-p| D[状态2]
    C --> E[随机游走]
    D --> E
    E -->|循环| B

在上面的流程图中，我们展示了马尔可夫链的随机游走过程。初始状态A经过一次转移概率B到达状态1或状态2，之后进入随机游走E，直到达到平稳分布。这个过程可以在R语言中通过编程实现，通过循环迭代来模拟马尔可夫链的行为。

## 3.2 R语言中的MCMC实现

### 3.2.1 使用R语言进行MCMC采样

在R语言中，我们可以利用一些现成的包来进行MCMC采样，例如`MCMCpack`和`coda`等。这些包提供了很多有用的函数，可以帮助我们构建马尔可夫链并进行采样。例如，使用`MCMCpack`包中的`MCMCmetrop1R`函数就可以实现基于Metropolis-Hastings算法的采样：

li