【R语言MCMC进阶教程】：深入学习贝叶斯线性回归与网络模型构建

# 1. R语言与MCMC入门

## 1.1 R语言简介

R语言是一种主要用于统计分析、图形表示和报告的编程语言。它因其强大的数据处理能力、丰富的统计方法以及包扩展性而被广泛用于学术研究和工业界。R语言拥有一个庞大的国际社区，不断有新的包和功能被开发出来，以支持各种复杂的数据分析任务。

## 1.2 MCMC方法概述

MCMC（Markov Chain Monte Carlo）是一种随机模拟算法，用于计算复杂统计模型中的数值解。它通过构建马尔可夫链来逼近感兴趣的高维概率分布，并最终用于估计模型参数或进行预测。MCMC方法特别适用于那些无法直接计算的模型，如贝叶斯推断中的后验分布。

## 1.3 R语言与MCMC的结合

在R语言中，存在多个包专门用于实现MCMC，如`coda`, `MCMCpack`, `rstan`等。这些包使得在R环境下进行MCMC分析变得十分方便。使用者可以利用R语言的函数和包轻松地进行数据分析、模型拟合以及结果展示。对于MCMC的初学者来说，R语言提供了一个良好的起点。

通过本章节的介绍，你将了解R语言的基础知识和MCMC方法的基本原理，为进一步学习贝叶斯线性回归和其它高级MCMC技术打下坚实的基础。

# 2. 贝叶斯线性回归理论与实践

## 2.1 贝叶斯线性回归基础

### 2.1.1 贝叶斯定理简介

贝叶斯定理，也称为贝叶斯规则，是概率论中的一个重要定理。它描述了在已知某些条件下，一个事件的概率如何根据相关条件概率来改变。其公式如下：

\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]

其中：

- \( P(A|B) \) 是在B发生的条件下A发生的条件概率。
- \( P(B|A) \) 是在A发生的条件下B发生的条件概率。
- \( P(A) \) 是事件A发生的边缘概率。
- \( P(B) \) 是事件B发生的边缘概率。

贝叶斯定理的关键在于，它允许我们通过条件概率来反推或者更新对A的信念。这一点在贝叶斯线性回归中尤为重要，因为它可以用来更新参数的后验分布。

### 2.1.2 线性回归模型回顾

线性回归是一种统计方法，用来建立一个变量（因变量）与一个或多个其他变量（自变量）之间的关系模型。简单线性回归模型可以表示为：

\[ Y = \beta_0 + \beta_1 X + \epsilon \]

其中：

- \( Y \) 是因变量。
- \( X \) 是自变量。
- \( \beta_0 \) 是截距。
- \( \beta_1 \) 是斜率。
- \( \epsilon \) 是误差项。

在实际应用中，通过最小化误差项的平方和来估计\( \beta_0 \) 和 \( \beta_1 \) 的值。然而，在贝叶斯线性回归中，我们不仅关心参数的最佳估计，还关心参数的不确定性。贝叶斯方法允许我们通过后验分布来量化这种不确定性。

## 2.2 MCMC算法原理

### 2.2.1 MCMC算法概述

马尔可夫链蒙特卡洛（MCMC）方法是一种基于模拟的计算算法，用于得到复杂分布的随机样本。MCMC算法的核心在于它构建了一个马尔可夫链，该链的平稳分布即为目标分布。算法从任意的初始状态开始，通过迭代地应用转移函数来探索目标分布的结构。

MCMC算法的典型步骤如下：

1. 选择一个合适的概率分布作为转移核（Transition Kernel），它决定了如何从当前状态转移到下一个状态。
2. 初始化参数。
3. 在每一步迭代中，根据转移核更新参数状态。
4. 经过足够多的迭代之后，链达到平稳分布，此时的参数抽样可以用来估计目标分布。

### 2.2.2 Gibbs采样与Metropolis-Hastings算法

Gibbs采样是MCMC方法中的一种特殊情况，它专门用于多变量分布的采样。Gibbs采样通过轮流抽取各分量变量来生成样本，每次只考虑其他分量的当前状态值，即：

\[ x^{(t+1)}_i \sim p(x_i|x^{(t+1)}_1, \ldots, x^{(t)}_{i-1}, x^{(t)}_{i+1}, \ldots, x^{(t)}_d) \]

其中\( d \)是变量的维数，\( t \)表示当前迭代步骤。

Metropolis-Hastings算法是另一种MCMC方法，它允许从任意目标分布中抽取样本。算法的关键在于接受比率（Acceptance Ratio），它决定了是否接受一个新状态。接受比率为：

\[ \alpha = \min\left(1, \frac{p(x_{\text{new}})q(x_{\text{old}}|x_{\text{new}})}{p(x_{\text{old}})q(x_{\text{new}}|x_{\text{old}})}\right) \]

其中\( p(x) \)是目标分布，\( q(\cdot|\cdot) \)是建议分布，用于从当前状态生成新状态。

## 2.3 R语言中的贝叶斯线性回归

### 2.3.1 使用R语言实现贝叶斯线性回归

在R语言中，我们可以使用各种贝叶斯统计包来实现贝叶斯线性回归。最流行的包之一是`rstanarm`或`brms`，它们都依赖于Stan语言来构建后验分布。以下是使用`brms`包进行贝叶斯线性回归的一个简单示例：

# 安装和加载brms包
if (!require("brms")) install.packages("brms")
library(brms)

# 使用brms进行贝叶斯线性回归
fit <- brm(y ~ x, data = mydata)

# 查看模型摘要
summary(fit)

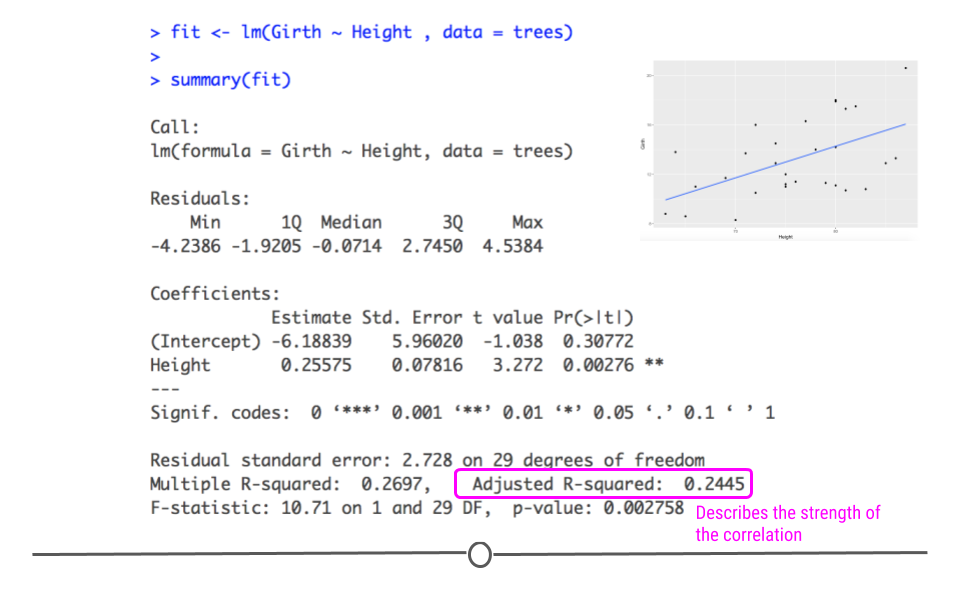
在上述代码中，我们首先检查并安装了`brms`包，随后使用该包的`brm`函数拟合了线性回归模型，并将结果存储在`fit`对象中。最后，我们通过`summary`函数来查看模型的详细摘要，包括参数的估计值、标准误、置信区间等。

### 2.3.2 模型结果解释与验证

拟合好贝叶斯线性回归模型之后，重要的是对结果进行解释和验证。模型摘要会提供参数的估计值，以及这些估计值的不确定性。在贝叶斯框架中，我们得到的是后验分布，而不仅仅是点估计值。

我们可以通过绘制参数的后验分布图来直观地展示结果：

# 绘制参数的后验分布图
plot(fit)

此外，还需要对模型进行诊断以验证其拟合的质量。我们可以检查残差的分布，检验模型预测与实际观测值之间的差异，以及评估链的混合情况和自相关性。通过这些验证步骤，我们可以确定模型是否可靠，以及是否需要进一步的模型调整。

# 检查链的混合情况
mcmc_trace(fit)

# 检查自相关性
mcmc_acf(fit)

# 检查残差图
residuals <- resid(fit)
plot(residuals ~ fitted(fit))

在上述代码块中，我们使用了`brms`包和`bayesplot`包的功能来进行模型诊断。通过这些诊断图，我们可以直观地了解模型的稳定性和准确性。

接下来，我们将进一步深入探讨高级MCMC技术及其在R语言中的应用。

# 3. 高级MCMC技术与应用

## 3.1 Hamiltonian Monte Carlo

### 3.1.1 HMC算法原理

Hamiltonian Monte Carlo（HMC）是一种基于物理学中的哈密顿动力学的算法，用于高效地探索多维参数空间，并生成MCMC样本。与传统的随机游走相比，HMC利用梯度信息来引导采样过程，使得在参数空间中的移动更加有效率，特别是在目标分布的形状复杂或者存在强相关性时。

HMC算法的核心思想是将参数看作系统的物理位置，将目标分布的对数看作势能，从而定义一个哈密顿能量函数。这个函数由动能项和势能项组成。动能项和势能项共同构成了哈密顿量（Hamiltonian），而MCMC的每一步则是通过对哈密顿量的模拟来实现的。

### 3.1.2 Stan与R语言的结合

Stan是一个专门用于贝叶斯统计分析的软件包，它提供了强大的HMC算法实现。在R语言中，可以借助`rstan`包来访问Stan的功能。`rstan`包为R用户提供了编写和运行Stan模型的接口，这使得R用户可以方便地使用HMC算法进行复杂模型的建模和参数推断。

使用`rstan`包时，用户首先需要安装和加载`rstan`，然后编写Stan模型的描述文件，这个文件是`.stan`格式的文本文件，其中包含了模型的统计结构。接着在R中读入这个模型，并使用`stan()`函数来运行模型，生成MCMC样本。

# 安装并加载rstan包
install.packages("rstan", dependencies = TRUE)
library(rstan)

# 编写Stan模型文件（例如：model.stan）
# model {
#   // ... Stan代码 ...
# }

# 读取模型文件
model_code <- readLines("model.stan")

# 编译模型
fit <- stan_model(model_code = model_code)

# 运行模型生成MCMC样本
samples <- sampling(fit, ..