【R语言MCMC包使用技巧】：链收敛性分析与优化策略

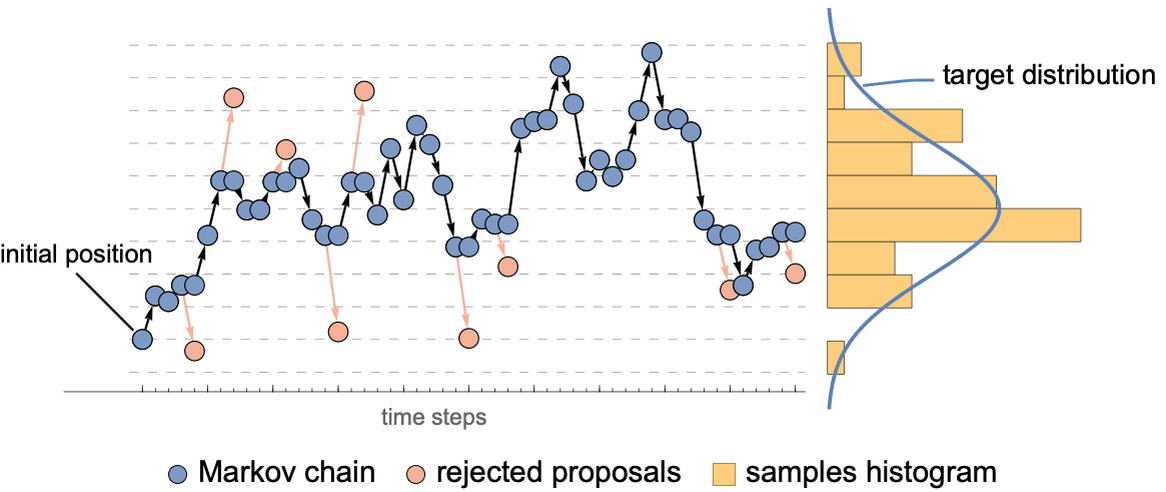
# 1. R语言MCMC包概述

MCMC包是R语言中用于执行蒙特卡洛模拟的重要工具包，它集成了多种MCMC（Markov Chain Monte Carlo）算法，以解决复杂统计模型中的参数估计问题。MCMC方法是一种统计学上的模拟技术，通过构造马尔可夫链来生成目标分布的样本。这些样本随后可用于估计复杂的多维概率分布、计算积分、优化问题等。在R语言环境中，MCMC包提供了一种直观和灵活的途径，允许用户轻松实施MCMC算法，并对结果进行分析和解释。本章将初步介绍MCMC包的安装、配置，以及如何使用这些工具来执行基本的MCMC模拟任务。

# 2. MCMC算法基础

### 2.1 马尔可夫链与蒙特卡洛方法

#### 2.1.1 马尔可夫链的基本原理
在统计学和概率论中，马尔可夫链是一类特殊的随机过程，由俄国数学家Andrey Markov提出。其核心特性是系统当前状态的统计特性只与前一个状态有关，与更早的状态无关，即所谓的无记忆性。形式上，马尔可夫链可以表述为一个状态转移概率矩阵，矩阵中的元素 \( P_{ij} \) 表示从状态 \( i \) 转移到状态 \( j \) 的概率。

在MCMC（Markov Chain Monte Carlo）算法中，我们利用马尔可夫链来生成一系列依赖于当前状态的随机样本，这些样本构成马尔可夫链的轨迹。由于马尔可夫链的性质，当链足够长且达到稳定状态时，这些样本的分布近似于目标分布，这样就可以用于各种统计推断问题。

#### 2.1.2 蒙特卡洛方法在统计推断中的应用
蒙特卡洛方法是一类以随机抽样为基础的计算方法。它通过模拟随机过程，计算各种统计量的期望值，从而用于解决数学问题和工程问题。在统计推断中，蒙特卡洛方法可以用来计算复杂概率分布下的积分问题，例如后验分布的期望值或者边缘概率分布。

举一个简单的例子，考虑一个后验分布的期望值计算问题。我们可以使用蒙特卡洛方法来估计它，即从后验分布中抽取大量的样本，然后计算这些样本的算术平均值。根据大数定律，当样本量足够大时，样本的平均值将接近期望值。

### 2.2 MCMC算法的理论框架

#### 2.2.1 接受-拒绝采样
接受-拒绝采样是一种基本的蒙特卡洛方法，它通过“建议分布”来生成服从目标分布的样本。这种方法的核心思想是，我们首先从一个较为容易抽样的建议分布中抽取一个样本，然后根据目标分布与建议分布的比值来决定是否“接受”这个样本。

具体来说，假设我们有一个目标分布 \( f(x) \) 和一个建议分布 \( g(x) \)，以及一个常数 \( c \) 使得对于所有的 \( x \)，都有 \( c \cdot g(x) \geq f(x) \)。接受-拒绝采样的算法步骤如下：

1. 从 \( g(x) \) 抽取 \( x \)。
2. 从均匀分布 \( U(0, 1) \) 抽取一个随机数 \( u \)。
3. 如果 \( u \leq \frac{f(x)}{c \cdot g(x)} \)，则接受 \( x \) 作为一个样本；否则，拒绝 \( x \) 并返回步骤1。

#### 2.2.2 Metropolis-Hastings算法
Metropolis-Hastings算法是一种更为通用的MCMC算法，它允许从任意的概率分布中抽取样本。Metropolis-Hastings算法的关键在于选择一个适当的转移核（或称为建议分布），该转移核能够保证链的平稳分布为目标分布。

算法步骤如下：

1. 初始化：选择一个初始状态 \( x_0 \)。
2. 迭代：
a. 给定当前状态 \( x_t \)，从转移核 \( q(x_t | x_{t-1}) \) 中抽取一个候选状态 \( x' \)。
b. 计算接受概率 \( \alpha(x_t, x') = \min \left(1, \frac{f(x')q(x_{t-1}|x')}{f(x_{t-1})q(x'|x_{t-1})}\right) \)，其中 \( f(x) \) 是目标分布。
c. 以概率 \( \alpha(x_t, x') \) 接受 \( x' \) 作为新的状态 \( x_{t+1} \)；否则，保持 \( x_{t+1} = x_t \)。

#### 2.2.3 Gibbs采样
Gibbs采样是另一种常用的MCMC算法，特别适用于多变量分布的采样问题。Gibbs采样通过依次对每个变量进行采样，来生成整个变量空间的样本。这种方法假设我们可以容易地从每个变量的条件分布中抽取样本。

Gibbs采样的算法步骤如下：

1. 初始化：为每一个变量 \( x_1, x_2, ..., x_n \) 选择初始值。
2. 迭代：
a. 对于每个 \( i = 1, ..., n \)，从条件分布 \( P(x_i | x_{-i}) \) 中抽取 \( x_i \) 的新值，其中 \( x_{-i} \) 表示除了 \( x_i \) 以外的其他变量的当前值。

Gibbs采样特别适合高维问题，因为每次只更新一个维度的值，从而简化了计算过程。但同时也存在局限性，比如对于某些条件分布的采样可能是困难的，或者对于变量之间的依赖关系过于紧密时收敛速度可能会很慢。

在下一章节中，我们将深入探讨MCMC包的安装与配置，以及如何为MCMC模拟设置正确的初始条件。

# 3. MCMC包的安装与配置

在本章节中，我们将深入探讨如何在R环境中安装和配置MCMC包，为后续的MCMC模拟打下基础。我们将从R语言环境的设置开始，逐步介绍MCMC包安装的具体步骤，以及如何配置MCMC模拟的初始