【R语言MCMC数据分析】：克服参数估计挑战，提升模型验证效能

# 1. R语言与MCMC数据分析概述

在现代数据分析领域中，R语言凭借其强大的统计计算能力及丰富的第三方包支持，已经成为不可或缺的工具之一。MCMC（Markov Chain Monte Carlo，马尔可夫链蒙特卡洛）作为一种统计模拟方法，尤其在贝叶斯推断框架中扮演着核心角色。本章将简要介绍R语言及其在MCMC数据分析中的应用概况，为后续章节打下坚实的基础。

## 1.1 R语言在数据分析中的地位

R语言自1990年代初问世以来，因其开源、灵活、扩展性强等特点，迅速成长为统计分析师和数据科学家的首选。R提供了丰富的统计分析函数，便捷的数据操作方式，以及强大的图形展示能力。此外，R的社区活跃，有大量的开发者贡献了各种专用的包，使其在金融分析、生物统计、市场研究等诸多领域都有广泛的应用。

## 1.2 MCMC方法的重要性

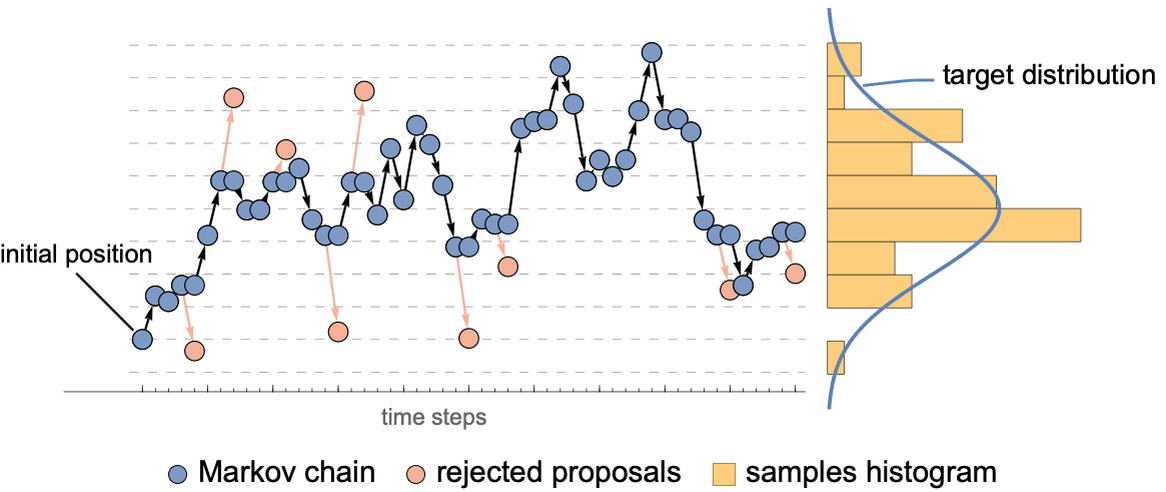
MCMC方法是一种利用随机抽样来解决复杂积分问题的技术，尤其是那些难以用传统数学方法解决的问题。它在概率模型的参数估计、预测以及模型比较中显示出巨大的潜力。MCMC方法的核心在于模拟一个马尔可夫链，以得到目标分布的样本，进而计算出分布的特征，比如期望值、方差、边缘概率等。

## 1.3 R语言与MCMC的结合

在R中集成MCMC方法，不仅可以提高数据处理的效率，还可以利用R的可视化能力，对模拟结果进行直观展示与分析。通过MCMC，用户可以对复杂模型的不确定性进行量化，这对进行科学决策和风险评估具有重要意义。在后续章节中，我们将深入探讨如何在R中实现MCMC数据分析，并分享一些实用的技巧和工具。

# 2. MCMC理论基础及其在数据分析中的应用

## 2.1 马尔可夫链蒙特卡洛方法（MCMC）简介

### 2.1.1 马尔可夫链的原理

马尔可夫链是马尔可夫过程的一种，其中的下一个状态仅依赖于当前状态，而不依赖于过去的历史。这可以用一个简单的数学定义来概括：如果一个系统在时间点n的状态为S(n)，那么下一个状态S(n+1)的出现仅依赖于S(n)，而不受S(n-1), S(n-2), ...等之前的任何状态影响。这使得马尔可夫链特别适合用来建模随时间变化的随机过程。

在MCMC中，马尔可夫链被用于生成后验分布的样本，这些样本可用于统计推断。由于直接从后验分布中抽样很难或不可能，马尔可夫链提供了一种间接方式来逼近这个分布。

### 2.1.2 蒙特卡洛方法的统计基础

蒙特卡洛方法利用随机抽样来解决问题和估计概率。在一个统计模型中，我们经常想评估一些难以直接计算的量，例如期望值、积分、概率或分布。蒙特卡洛方法可以通过从定义的分布中抽取大量样本，并使用这些样本来估计这些量。

举个例子，假设我们要计算一个复杂函数f(x)在区间[0,1]上的积分。我们可以从这个区间均匀抽取N个随机数，然后计算f(x)在这些点上的值。通过对这些函数值求平均，我们能够估计出积分的近似值。随着样本数N的增加，估计值的精度通常会提高。

当结合马尔可夫链和蒙特卡洛方法时，MCMC允许我们在复杂的高维后验分布上进行有效的蒙特卡洛模拟。它通过构建一个具有特定平稳分布的马尔可夫链来实现，这个平稳分布就是我们感兴趣的后验分布。

## 2.2 MCMC算法的种类及选择

### 2.2.1 常见的MCMC算法：Metropolis-Hastings, Gibbs采样

在MCMC的诸多算法中，Metropolis-Hastings和Gibbs采样是最为广泛应用的两种。

**Metropolis-Hastings算法**是一种通用的MCMC方法，它允许从任何可逆的马尔可夫链开始，只要该链满足详细的平衡条件。算法的基本步骤包括选择一个初始状态，然后通过模拟马尔可夫链的转移来生成新的状态。在每一步中，通过比较一个称为接受概率的随机数和一个特定阈值来决定是否接受新的状态。如果接受，状态转移；如果拒绝，状态保持不变。

**Gibbs采样**是一种特定于多变量分布的MCMC算法，特别适合于维度高的问题。在Gibbs采样中，不是一次性考虑所有参数的更新，而是轮流更新各个参数。在每一轮中，固定其他参数，只对一个参数进行采样。这样在每次迭代中可以保证采样来自联合后验分布。

### 2.2.2 算法比较及选择标准

选择合适的MCMC算法往往依赖于具体问题的特性。Metropolis-Hastings算法因其灵活性而广泛应用于各种问题中，特别是当后验分布复杂或不完全已知时。Gibbs采样更适合于参数之间的相互依赖关系较为简单的情况。

在实际应用中，算法的选择也通常受数据维度、计算资源和目标分布特性的影响。在某些情况下，混合算法或者自适应算法可能更合适。总的来说，算法选择需要权衡样本的生成速度、分布的准确性、以及实现的复杂性等因素。

## 2.3 MCMC在参数估计中的应用

### 2.3.1 参数估计的概念和重要性

参数估计是统计学的核心问题之一，其目标是从观测数据中估计模型参数的未知值。参数估计在实际应用中极为重要，因为参数值不仅影响模型预测，还关系到模型是否能够真实反映实际现象。

在经典的统计推断框架中，参数估计的方法分为点估计和区间估计。点估计提供一个单一的值来估计参数，而区间估计提供一个区间范围，其中参数的真值有一定概率位于该区间内。

### 2.3.2 MCMC在参数估计中的优势和挑战

MCMC方法在参数估计中的优势主要体现在可以处理复杂模型和非标准分布。特别是当遇到无法直接得到解析解的模型时，MCMC提供了强大的数值计算能力。此外，MCMC能有效地处理高维参数空间和复杂的依赖结构。

不过，使用MCMC也面临一些挑战，例如收敛性问题。在迭代过程中，马尔可夫链可能需要较长时间才能收敛到目标后验分布。这要求研究者仔细设计MCMC算法，并进行适当的诊断测试以确保收敛性。

此外，MCMC通常需要大量的迭代才能获得足够数量的样本以进行可靠的估计，这导致计算成本较高。如何高效地抽取样本并减少自相关性，是MCMC应用中的另一个挑战。尽管如此，MCMC在参数估计中的应用依然广泛，特别是在贝叶斯统计领域。

# 3. R语言实现MCMC分析的工具与技巧

## 3.1 R语言中的MCMC工具包

### 3.1.1 掌握coda、MCMCpack等包的基本使用

在R语言中，实现MCMC分析的工具包有很多，其中比较著名的有`coda`和`MCMCpack`。`coda`包主要用于MCMC模拟结果的诊断和后处理，提供了丰富的函数来进行迹图绘制、自相关分析、有效样本大小的计算等。而`MCMCpack`则提供了实现各种MCMC算法的函数，它更侧重于模型的模拟。

要开始使用这些工具包，首先需要安装并加载它们。以下是一个基本示例：

# 安装coda和MCMCpack包
install.packages("coda")
install.packages("MCMCpack")

# 加载包
library(coda)
library(MCMCpack)

接下来，我们可以使用`MCMCpack`包中的`MCMCregress`函数来执行一个简单的线性回归模拟：

# 使用MCMCregress函数进行贝叶斯线性回归模拟
set.seed(123)  # 设置随机数种子以便重现结果
mcmc_results <- MCMCregress(y ~ x, data = mydata, burnin = 1000, mcmc = 5000, thin = 10)

# 将模拟结果转换为mcmc对象以便使用coda包的功能
coda_results <- as.mcmc(mcmc_results)

### 3.1.2 评估不同工具包的性能和适用场景

不同的MCMC工具包在性能和适用性方面有所差异，`coda`和`MCMCpack`虽然功能强大，但在面对复杂的多参数模型时，可能需要更多的自定义和调优。对于这类问题，`rjags`和`nimble`这样的包提供了更多的灵活性，允许用户使用JAGS或NIMBLE语言编写自己的MCMC算法。

在选择工具包时，建议根据以下几个方面进行评估：

- **模型支持**：某些包可能更适合特定类型的模型，如贝叶斯逻辑回归或生存分析。
- **性能要求**：考虑模型的规模和复杂性。大型模型可能需要并行计算和高效的算法。
- **用户友好性**：接口的易用性及文档和社区支持