傅里叶变换进阶指南：圆域函数边界条件的智慧处理


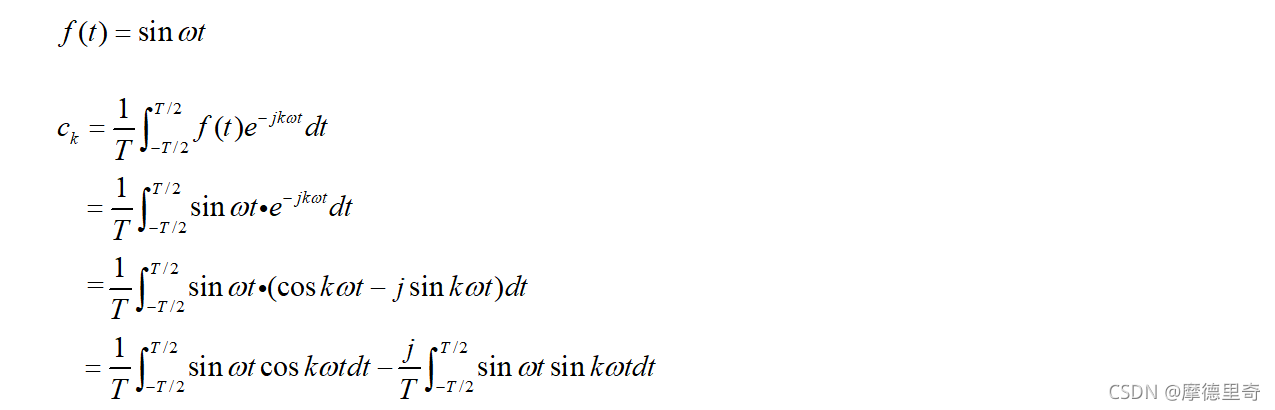
# 摘要
本文对傅里叶变换及其在圆域函数边界条件处理中的应用进行了全面的回顾和深入的探讨。第一章对傅里叶变换的基本概念进行了基础回顾，为后续章节的深入研究奠定了基础。第二章详细分析了圆域函数的特性以及边界条件的定义、分类和作用，并探讨了边界条件的处理方法。第三章进一步深化了理论，并通过傅里叶级数和离散傅里叶变换（DFT）的实践应用，展示了傅里叶变换在圆域函数中的重要性。同时，介绍了快速傅里叶变换（FFT）及其优化策略。第四章专门讨论了边界条件处理的高级技巧，包括数值解法、误差分析与控制以及软件工具的应用。最后，第五章提出了解决圆域函数边界条件问题的创新方法，并通过实验验证了其有效性和实际应用前景。本文综合了理论分析和应用实例，为圆域函数的边界条件处理提供了新的视角和解决方案。

# 关键字
傅里叶变换；圆域函数；边界条件；数值解法；误差分析；软件工具

参考资源链接：[圆域函数傅里叶变换详解：贝塞尔函数与常见信号的频谱解析](https://wenku.csdn.net/doc/6qsypjzw3w?spm=1055.2635.3001.10343)
# 1. 傅里叶变换基础回顾

## 1.1 傅里叶变换的历史和意义
傅里叶变换是数学领域中一种极为重要的分析工具，由法国数学家让-巴蒂斯特·约瑟夫·傅里叶提出。其核心思想是任何周期函数都可以表示为不同频率的正弦波的叠加，这一理论对后续的信号处理、图像分析、量子物理等领域产生了深远影响。傅里叶变换将复杂的问题简化为频域问题，使得在频域中分析和处理数据更为直观和高效。

## 1.2 傅里叶变换的基本概念
傅里叶变换将时域信号转换为频域信号，包含连续和离散两种形式。连续傅里叶变换（Continuous Fourier Transform, CFT）用于连续信号，其公式为：

F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} dt

而离散傅里叶变换（Discrete Fourier Transform, DFT）用于离散信号，公式为：

F(k) = \sum_{n=0}^{N-1} f(n) e^{-i 2 \pi k n / N}

其中，\(f(t)\)和\(f(n)\)代表时域信号，\(F(\omega)\)和\(F(k)\)代表对应的频域信号。

## 1.3 傅里叶变换的实际应用
在实际应用中，快速傅里叶变换（Fast Fourier Transform, FFT）是DFT的高效实现，极大降低了计算复杂度，这使得傅里叶变换在各种信号处理场合中变得可行。例如，在数字信号处理中，FFT广泛用于频谱分析、信号滤波和数据压缩等领域。在图像处理中，傅里叶变换帮助我们理解和操作图像的空间频率成分，对于图像增强、压缩和特征提取具有重要作用。

通过本章的回顾，我们为理解更复杂的圆域函数及其边界条件打下了坚实的理论基础。接下来，我们将深入了解圆域函数与边界条件，继续探索傅里叶变换在其中的应用与优化。

# 2. 圆域函数与边界条件

## 2.1 圆域函数的特性分析

### 2.1.1 定义与分类

圆域函数是一类在圆域上定义的函数，它们通常表示为角度或弧度的函数。这类函数在物理学、工程学以及信号处理等领域有着广泛的应用。按照定义域的不同，圆域函数可以分为周期性圆域函数和非周期性圆域函数。周期性圆域函数的值在某个周期内重复出现，而非周期性圆域函数则在定义域内具有唯一的值。根据函数表达式的特性，圆域函数还可以细分为连续圆域函数和离散圆域函数。

### 2.1.2 圆域函数的数学表达

数学上，圆域函数可以通过三角函数展开为无穷级数。这种展开形式是傅里叶级数的基础，它将复杂的圆域函数表达为一系列正弦和余弦函数的和。例如，函数f(θ)在圆域上的展开可以表示为：

\[ f(θ) = a_0 + \sum_{n=1}^{\infty} [a_n \cos(nθ) + b_n \sin(nθ)] \]

其中，\( a_n \) 和 \( b_n \) 是傅里叶系数，它们通过积分计算得到。这个表达式不仅揭示了圆域函数的内在结构，还为边界条件的处理提供了数学基础。

## 2.2 边界条件的引入

### 2.2.1 边界条件的概念

边界条件是指在数学物理问题中，描述解在边界上应满足的条件。对于圆域函数来说，边界条件通常指函数在圆周上的值或者其导数在边界上的性质。这些条件是求解偏微分方程和积分方程的关键部分，它们能够影响到解的唯一性和稳定性。

### 2.2.2 边界条件在圆域函数中的作用

在圆域函数的分析和计算中，边界条件起到决定性的作用。例如，在电磁学中，一个圆形区域内的电势分布可以通过求解拉普拉斯方程得到，而边界上的电势值正是定义边界条件的关键参数。边界条件不仅限定了问题的物理范围，还帮助我们在数学上缩小了解的搜索空间，从而得到精确的数学表达式。

## 2.3 边界条件处理方法

### 2.3.1 常规方法介绍

在处理圆域函数的边界条件时，常规方法包括直接替换、迭代逼近、分离变量法等。直接替换是将边界条件直接代入到圆域函数的表达式中，以此获得满足边界条件的特定解。迭代逼近则涉及到不断更新函数值直到满足边界条件为止。分离变量法则是将变量分解为独立部分，以简化边界条件问题的求解。

### 2.3.2 高级处理技巧

边界条件的高级处理技巧包括格林函数法和变分法。格林函数法通过构建一个与边界条件相关的特殊函数来简化边界问题的求解过程。变分法则是通过最小化能量泛函的方式来求解边界条件问题，这种方法在处理复杂边界条件时显示出其独特的优势。

### 表格：边界条件处理方法对比

| 方法 | 适用范围 | 精度 | 计算复杂度 | 示例 |
| --- | --- | --- | --- | --- |
| 直接替换 | 简单问题 | 较低 | 低 | 电磁学中的电势计算 |
| 迭代逼近 | 稍复杂问题 | 中等 | 中等 | 热传导方程的求解 |
| 分离变量法 | 中等复杂问题 | 较高 | 中等 | 弹性理论中的振动模式分析 |
| 格林函数法 | 复杂边界条件 | 高 | 高 | 量子力学中的粒子散射问题 |
| 变分法 | 高级应用 | 高 | 高 | 结构优化中的应力分析 |

通过上表可以看出，不同的边界条件处理方法适用于不同复杂度的问题，并且在精度和计算复杂度上各有优劣。选择合适的方法对于求解特定问题至关重要。

### 代码块：傅里叶级数在Python中的实现

import numpy as np

# 定义圆域函数
def circle_function(theta):
    return np.sin(theta) + 0.5 * np.sin(2 * theta)

# 计算傅里叶系数
def