傅里叶变换:圆域函数优化算法,提升性能的金钥匙
发布时间: 2024-12-26 10:40:21 阅读量: 7 订阅数: 10 


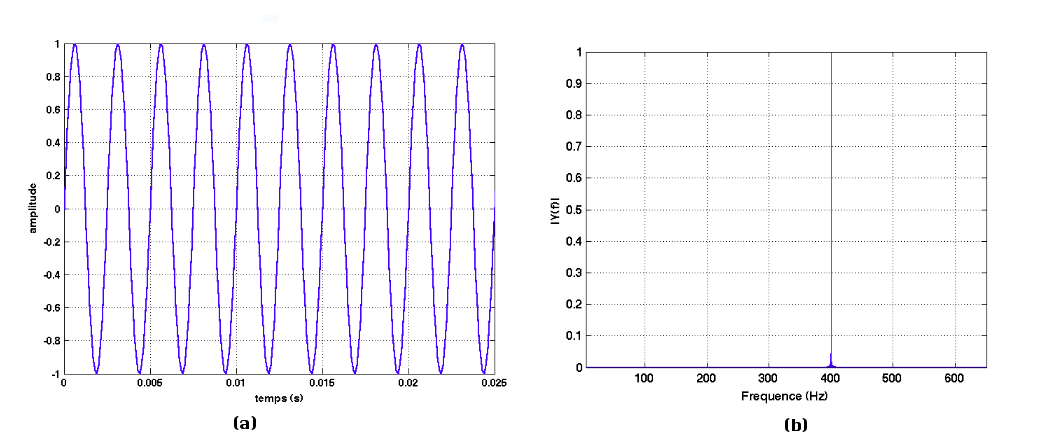
Rect函数的傅里叶变换:Rect函数的傅里叶变换-matlab开发
# 摘要
本文旨在探讨傅里叶变换理论及其与圆域函数的联系,并分析其在信号和图像处理中的应用实践。通过深入研究傅里叶变换的基本原理,包括傅里叶级数与圆域函数的关系,本文阐述了连续傅里叶变换和离散傅里叶变换(DFT)及其快速算法(FFT)的实现方法。针对圆域函数优化算法,文章探讨了其在去噪、滤波、压缩、重构以及图像增强等应用,并对优化策略和性能提升技术进行了详细论述。最后,本文展望了圆域函数优化算法的未来发展方向,以及技术进步和新兴算法在其中的作用,为相关领域的研究人员和工程师提供了深入的理论知识和实践指导。
# 关键字
傅里叶变换;圆域函数;信号处理;图像处理;算法优化;FFT算法
参考资源链接:[圆域函数傅里叶变换详解:贝塞尔函数与常见信号的频谱解析](https://wenku.csdn.net/doc/6qsypjzw3w?spm=1055.2635.3001.10343)
# 1. 傅里叶变换理论基础
## 1.1 傅里叶变换的数学定义
傅里叶变换是一种将函数从时域转换到频域的数学方法,它能够揭示信号在频率上的组成。一个连续函数\( f(t) \)的傅里叶变换定义为:
\[
F(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-i \omega t} \, dt
\]
其中,\( F(\omega) \)代表了\( f(t) \)在各个频率分量上的幅度和相位信息。
## 1.2 从时域到频域的转换
傅里叶变换的核心思想在于将复杂的时域信号分解为简单的正弦波组合。通过这种转换,时域中难以观察和处理的信号特性在频域中变得清晰可见。例如,信号中的周期性噪声或特定频率的干扰更容易在频域中被识别和处理。
## 1.3 傅里叶变换的应用领域
傅里叶变换广泛应用于信号处理、图像处理、通信系统等领域。通过频域分析,工程师能够更好地对信号进行滤波、压缩、编码等操作,从而提高信号处理的质量和效率。
# 2. 圆域函数与傅里叶变换的联系
在了解傅里叶变换之前,首先要了解它的应用背景和基础,也就是圆域函数。本章节我们将探讨圆域函数的基本概念、傅里叶级数与圆域函数的关系,以及实现傅里叶变换的具体方法。
## 2.1 圆域函数的基本概念
### 2.1.1 定义和分类
圆域函数是定义在圆周或球面上的函数,常被用于描述周期信号或进行信号的频域分析。圆域函数主要分为两类:周期函数和非周期函数。周期函数具有固定周期,而非周期函数则没有明显的周期性。
### 2.1.2 圆域函数在信号处理中的重要性
在信号处理领域,圆域函数的重要性在于其能够将复杂的周期信号简化成一系列的正弦波和余弦波的叠加,这些基本波形可以使用傅里叶级数进行分析和处理。傅里叶级数是傅里叶变换的理论基础,通过它,可以将周期函数分解为简单的正弦和余弦函数的无穷和。
## 2.2 傅里叶级数与圆域函数
### 2.2.1 傅里叶级数的数学原理
傅里叶级数允许我们将周期函数表示为不同频率的正弦和余弦函数的无限和。每一个正弦和余弦函数称为一个谐波,它们具有不同的频率和幅度。
### 2.2.2 圆域函数与傅里叶级数的关系
圆域函数可以借助傅里叶级数,将其展开为多个谐波的和。这一过程的核心是找出每个谐波的系数,这些系数与原函数的特性密切相关。傅里叶级数的展开本质上是将周期函数映射到频域上,为频域分析提供了可能。
## 2.3 傅里叶变换的实现方法
### 2.3.1 连续傅里叶变换
连续傅里叶变换是将连续时间信号从时域转换到频域的数学工具。对于任意信号 \(f(t)\),其连续傅里叶变换定义为:
\[ F(\omega) = \int_{-\infty}^{\infty} f(t) e^{-j \omega t} dt \]
其中,\( F(\omega) \) 表示 \( f(t) \) 在频率 \(\omega\) 上的频谱表示。
### 2.3.2 离散傅里叶变换(DFT)及其快速算法(FFT)
离散傅里叶变换是连续傅里叶变换在数字信号处理中的等效形式,用于分析离散时间序列。DFT的计算复杂度较高,因此引入了快速傅里叶变换(FFT)来提高计算效率。FFT是DFT的一种快速实现算法,通过分治法或蝶形算法来减少计算量。FFT算法的基本步骤如下:
```python
import numpy as np
def fft(x):
N = len(x)
if N <= 1: return x
even = fft(x[0::2])
odd = fft(x[1::2])
T = [np.exp(-2j * np.pi * k / N) * odd[k] for k in range(N // 2)]
return [even[k] + T[k] for k in range(N // 2)] + [even[k] - T[k] for k in range(N // 2)]
# 示例输入信号
x = np.array([0.0, 1.0, 0.0, -1.0])
# 执行FFT算法
X = fft(x)
print(X)
```
上面的代码展示了如何使用Python中的NumPy库来实现FFT算法。首先,对于输入信号 \( x \),我们将其分为偶数索引部分和奇数索引部分,然后分别计算这两个部分的FFT。最后,将这两部分合并在一起来计算最终的FFT结果。
在接下来的章节中,我们将深入探讨傅里叶变换在信号处理和图像处理中的应用,并通过实例来了解圆域函数优化算法的实际应用。
# 3. ```
# 第三章:圆域函数优化算法的实践应用
圆域函数优化算法是将数学理论应用到实际问题中的关键所在,特别是在信号和图像处理领域,这些算法能够大幅度提升数据处理的效率和质量。本章将详细介绍傅里叶变换在信号处理和图像处理中的应用,并通过实际案例分析展示其优化效果。
## 3.1 傅里叶变换在信号处理中的应用
### 3.1.1 信号去噪和滤波
信号去噪是信号处理中的一项基础任务,其目的是减少信号中不需要的成分,通常是由外部噪声引起的。傅里叶变换提供了一种有效的方法来分离信号和噪声。
应用傅里叶变换进行信号去噪通常包括以下几个步骤:
1. 将信号从时域转换到频域。
2. 利用频域中的特性,如噪声和信号的频率特性不同,设计滤波器。
3. 应用滤波器,将噪声频率分量去除或减弱。
4. 将处理后的频域信号转换回时域。
```python
import numpy as np
import matplotlib.pyplot as plt
from scipy.fft import fft, ifft
# 示例信号
t = np.linspace(0, 1, 500, endpoint=False)
signal = np.sin(2 * np.pi * 10 * t) + 0.5 * np.sin(2 * np.pi * 50 * t)
# 添加噪声
noisy_s
0
0





