频率响应与稳定性分析


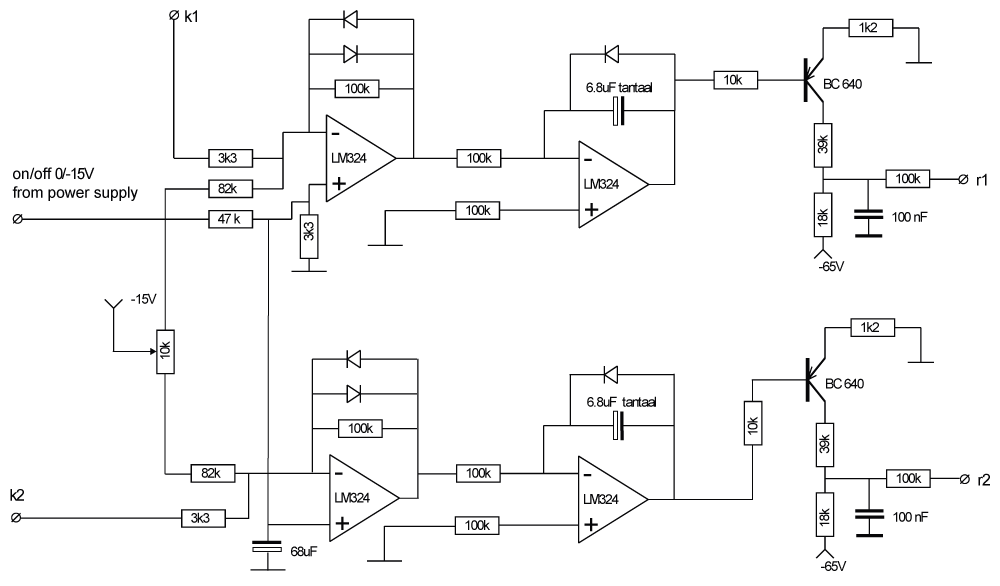
参考资源链接：[LM324函数发生器设计：方波、三角波、正弦波](https://wenku.csdn.net/doc/7hrir3diyq?spm=1055.2635.3001.10343)
# 1. 频率响应与稳定性分析基础

## 1.1 什么是频率响应？
频率响应指的是系统对不同频率输入信号的响应特性。它是衡量控制系统在各个频率点上的性能指标，通常用幅度比（增益）和相位差来描述。理解频率响应对于控制系统的设计和分析至关重要，因为它直接关系到系统的稳定性和动态性能。

## 1.2 频率响应的重要性
系统在实际应用中往往会遇到各种频率的信号，频率响应能够展示系统对这些不同信号的处理能力。通过分析频率响应，工程师可以优化系统设计，确保在特定频率范围内的信号得到正确的放大、减小或者相位调整，从而达到设计要求。

## 1.3 频率响应与系统稳定性的关系
频率响应不仅反映了系统对频率的敏感程度，也是评估系统稳定性的一个关键因素。一个良好的频率响应曲线应当没有过多的峰值，以免在运行时因信号的微小变化导致系统振荡。在分析系统稳定性时，频率响应方法（例如Bode图）可以直观地展示系统是否稳定，以及如何通过调整设计参数来增强系统的稳定性。

# 2. 控制系统理论基础

### 2.1 控制系统的数学模型

#### 2.1.1 线性时不变系统的模型

线性时不变（Linear Time-Invariant，LTI）系统的数学模型是研究控制系统的基础，它将系统的输入和输出之间的关系用数学语言进行描述。LTI系统具有两个关键特性：线性和时不变性。线性意味着系统满足叠加原理，即系统的两个输入的线性组合产生的输出，等于这两个输入各自产生的输出的同样线性组合。时不变性指的是系统对时间的响应不随时间改变而改变。

对于一个连续时间的LTI系统，其数学模型通常用微分方程来表示。假设系统的输入为u(t)，输出为y(t)，则可以写出如下的n阶线性常微分方程：

\[ a_0 \frac{d^n y(t)}{dt^n} + a_1 \frac{d^{n-1} y(t)}{dt^{n-1}} + ... + a_n y(t) = b_0 \frac{d^m u(t)}{dt^m} + b_1 \frac{d^{m-1} u(t)}{dt^{m-1}} + ... + b_m u(t) \]

其中，\(a_i\) 和 \(b_i\) 是常数系数，m 和 n 分别是输入和输出微分方程的阶数。通过拉普拉斯变换，可以将微分方程转化为代数方程，这在频域分析中非常有用。

#### 2.1.2 状态空间表示法

状态空间表示法（State-Space Representation）是描述控制系统动态行为的另一种数学模型。它由一组一阶微分方程表示，能够描述系统的动态变化过程。状态空间模型包括状态方程和输出方程：

\[ \dot{x}(t) = Ax(t) + Bu(t) \]
\[ y(t) = Cx(t) + Du(t) \]

其中，\(x(t)\) 是系统的状态向量，\(u(t)\) 是输入向量，\(y(t)\) 是输出向量，\(A\)、\(B\)、\(C\)、\(D\) 是与系统相关的矩阵。

状态空间模型的优势在于它能够更直观地反映系统的内部状态，适合计算机分析和设计控制策略。矩阵\(A\)是系统矩阵，描述了系统内部动态；矩阵\(B\)是输入矩阵，描述了输入对系统状态的影响；矩阵\(C\)是输出矩阵，描述了系统状态如何影响输出；矩阵\(D\)是直接传递矩阵，代表输入直接对输出的影响。

### 2.2 系统的稳定性概念

#### 2.2.1 稳定性的定义和判据

稳定性是控制理论中一个核心概念，指的是系统在受到扰动或初始条件变化时，能否保持其性能。对于LTI系统而言，稳定性是指系统在没有持续外部输入的情况下，随着时间的推移，系统状态是否会趋于零。在频域中，稳定性也可以通过系统传递函数的极点位置来判定。如果系统传递函数的所有极点均位于复平面的左半部分，则该系统是稳定的。

#### 2.2.2 Lyapunov稳定性理论

Lyapunov稳定性理论提供了一种通过构造所谓的Lyapunov函数来判定系统稳定性的一般方法。Lyapunov函数是一个标量函数，它在系统平衡点的值达到最小，并且沿着系统的轨迹是非增的。如果能够找到这样的函数，则可以判定系统在平衡点附近是稳定的。

### 2.3 系统的频率特性

#### 2.3.1 频率响应的概念

频率响应描述了线性时不变系统对于不同频率输入信号的响应特性。它是系统在各个频率上增益和相位变化的函数，通常用来分析系统对周期信号的响应。频率响应可以通过傅里叶变换从系统的传递函数中得到。

#### 2.3.2 频率响应的计算方法

频率响应可以通过几种不同的方法来计算，包括解析方法和数值方法。解析方法主要依赖于系统的传递函数，通过在复频域内对传递函数进行分析来获得频率响应。数值方法则利用计算机模拟技术来获得频率响应，比如频率扫描分析。在MATLAB等软件中，可以通过特定的命令和函数来直接计算频率响应，例如`bode`函数可以绘制系统的Bode图，而`nyquist`函数则用来绘制Nyquist图。

# 3. 频率响应的分析方法

## 3.1 开环频率响应分析

### 3.1.1 Bode图的绘制和解读

Bode图是控制系统分析中应用最为广泛的工具之一，它将系统的开环传递函数分解为幅度图和相位图，从而直观地展示系统在不同频率下的增益特性和相位特性。Bode图的横坐标为频率（通常是对数坐标），纵坐标分别为增益（分贝）和相位（度或弧度）。

绘制Bode图通常涉及以下步骤：

1. 将开环传递函数转换为标准形式，即将其分解为一系列项的乘积，例如常数项、时间常数项、极点项、零点项等。
2. 根据每个项的特点，绘制其对应的幅频和相频特性。
3. 将各部分的特性曲线叠加，得到整个系统的Bode图。

解析Bode图时，我们可以关注以下几个关键指标：

- 增益交叉频率：系统增益下降到0dB时对应的频率，它影响系统的稳定性和带宽。
- 相位交叉频率：系统相位达到-180度时对应的频率，它与系统的相位裕度直接相关。
- 相位裕度：在增益交叉频率处，相位与-180度之间的差值，它表征系统的稳定性。

下面是绘制Bode图的一个简单示例：

% 定义开环传递函数
s = tf('s');
G = 1000 / (s*(s+10)*(s+100));

% 绘制Bode图
figure;
bode(G);
grid on;

### 3.1.2 Nyquist稳定判据

Nyquist稳定判据是一