连通分量在实际场景中的应用:从社交网络到图像处理,解锁现实世界中的神奇力量
发布时间: 2024-07-10 10:09:33 阅读量: 62 订阅数: 28 


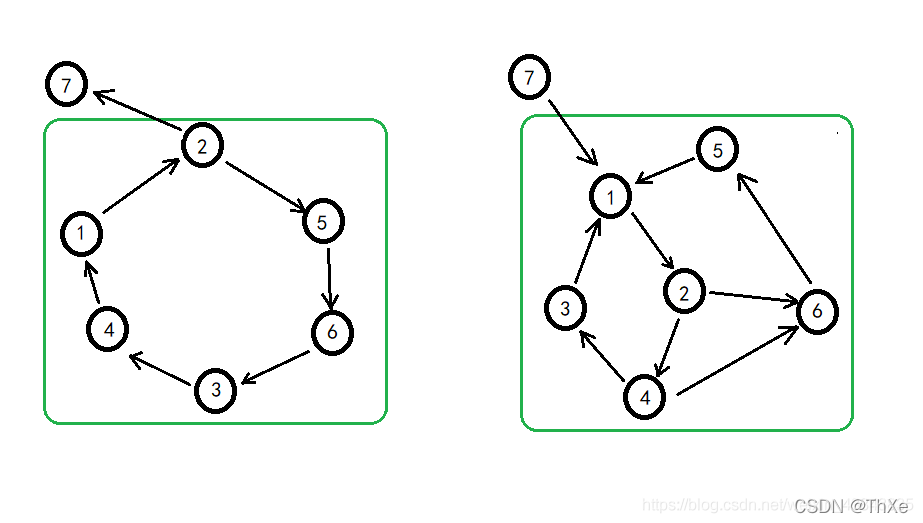
识别连通分量
# 1. 连通分量概述
**1.1 连通分量的定义**
连通分量是图论中一个重要的概念,它表示图中相互连接的顶点集合。两个顶点之间如果存在一条路径,则它们属于同一个连通分量。
**1.2 连通分量的性质**
连通分量具有以下性质:
* **最大性:**连通分量中包含了所有相互连接的顶点。
* **互斥性:**不同的连通分量之间没有共同的顶点。
* **覆盖性:**图中的所有顶点都属于某个连通分量。
# 2. 连通分量算法
连通分量算法用于识别图中相互连接的顶点集合,这些集合称为连通分量。连通分量算法有两种主要类型:深度优先搜索算法和广度优先搜索算法。
### 2.1 深度优先搜索算法
**2.1.1 基本原理**
深度优先搜索(DFS)算法从图中的一个顶点开始,递归地遍历所有与该顶点相邻的顶点。当没有更多相邻顶点可遍历时,算法回溯到前一个顶点,并继续从该顶点遍历。
**2.1.2 实现细节**
以下代码展示了 DFS 算法的实现:
```python
def dfs(graph, start):
"""
深度优先搜索算法
参数:
graph:图,表示为邻接表
start:起始顶点
"""
visited = set() # 存储已访问的顶点
stack = [start] # 存储待访问的顶点
while stack:
current = stack.pop() # 弹出栈顶元素
if current not in visited: # 如果该顶点未被访问过
visited.add(current) # 标记为已访问
for neighbor in graph[current]: # 遍历该顶点的相邻顶点
if neighbor not in visited: # 如果相邻顶点未被访问过
stack.append(neighbor) # 将相邻顶点压入栈中
```
**代码逻辑分析:**
* 初始化一个集合 `visited` 来存储已访问的顶点,并初始化一个栈 `stack` 来存储待访问的顶点。
* 从起始顶点开始,将其压入栈中。
* 循环遍历栈,弹出栈顶元素 `current`。
* 如果 `current` 未被访问过,则将其标记为已访问,并将其所有相邻顶点压入栈中。
* 重复上述步骤,直到栈为空。
### 2.2 广度优先搜索算法
**2.2.1 基本原理**
广度优先搜索(BFS)算法从图中的一个顶点开始,逐层遍历所有与该顶点相邻的顶点。当遍历完该层的所有顶点后,再遍历下一层顶点。
**2.2.2 实现细节**
以下代码展示了 BFS 算法的实现:
```python
def bfs(graph, start):
"""
广度优先搜索算法
参数:
graph:图,表示为邻接表
start:起始顶点
"""
visited = set() # 存储已访问的顶点
queue = [start] # 存储待访问的顶点
while queue:
current = queue.pop(0) # 弹出队列首元素
if current not in visited: # 如果该顶点未被访问过
visited.add(current) # 标记为已访问
for neighbor in graph[current]: # 遍历该顶点的相邻顶点
if neighbor not in visited: # 如果相邻顶点未被访问过
queue.append(neighbor) # 将相邻顶点加入队列尾部
```
**代码逻辑分析:**
* 初始化一个集合 `visited` 来存储已访问的顶点,并初始化一个队列 `queue` 来存储待访问的顶点。
* 从起始顶点开始,将其加入队列中。
* 循环遍历队列,弹出队列首元素 `current`。
* 如果 `current` 未被访问过,则将其标记为已访问,并将其所有相邻顶点加入队列尾部。
* 重复上述步骤,直到队列为空。
# 3. 连通分量在社交网络中的应用
### 3.1 社交网络中的社群发现
#### 3.1.1 社群的定义和特点
在社交网络中,社群是指一群具有共同兴趣、爱好或社会关系的人。社群通常具有以下特点:
* **成员之间的联系紧密:**社群成员之间存在频繁的互动,如发消息、评论、点赞等。
* **内部结构稳定:**社群成员之间的联系相对稳定,不会轻易发生变化。
* **外部联系较少:**社群成员与外部成员的联系相对较少,形成一个相对独立的群体。
#### 3.1.2 连通分量算法在社群发现中的应用
连通分量算法可以用来发现社交网络中的社群。算法的基本思想是:
1. 将社交网络表示为一个图,其中节点代表用户,边代表用户之间的关系。
2. 运行连通分量算法,将图中的节点划分为不同的连通分量。
3. 每个连通分量代表一个社群,社群中的成员之间具有紧密的联系。
### 3.2 社交网络中的影响力分析
#### 3.2.1 影响力度量的指标
社交网络中影响力通常用以下指标来衡量:
* **度中心性:**度中心性衡量一个节点与其他节点的连接数量。度中心性高的节点通常具有较大的影响力。
* **接近中心性:**接近中心性衡量一个节点到其他所有节点的平均距离。接近中心性高的节点通常可以快速传播信息。
* **介数中心性:**介数中心性衡量一个节点在其他节点之间的信息传递中所起的作用。介数中心性高的节点通常是信息传播的枢纽。
#### 3.2.2 连通分量算法在影响力分析中的应用
连通分量算法可以用来分析社交网络中的影响力。算法的基本思想是:
1. 将社交网络表示为一个图,其中节点代表用户,边代表用户之间的关系。
2. 运行连通分量算法,将图中的节点划分为不同的连通分量。
3. 计算每个连通分量中节点的影响力指标。
4. 连通分量中影响力指标较高的节点通常是该社群中具有较大影响力的人物。
```python
import networkx as nx
# 创建一个社交网络图
G = nx.Graph()
G.add_nodes_from(['A', 'B', 'C', 'D', 'E', 'F', 'G'])
G.add_edges_from([('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'E'), ('E', 'F'), ('F', 'G')])
# 运行连通分量算法
components = nx.connected_components(G)
# 计算每个连通分量中节点的影响力指标
for component in components:
for node in component:
degree_centrality = nx.degree_centrality(G)[node]
closeness_centrality = nx.closeness_centrality(G)[node]
betweenness_centrality = nx.betweenness_centrality(G)[node]
print(f"节点 {node} 的度中心性:{degree_centrality}")
print(f"节点 {node} 的接近中心性:{closeness_centrality}")
print(f"节点 {node} 的介数中心性:{betweenness_centrality}")
```
**代码逻辑分析:**
* `nx.connected_components(G)`:运行连通分量算法,将图划分为不同的连通分量。
* `nx.degree_centrality(G)`:计算图中每个节点的度中心性。
* `nx.closeness_centrality(G)`:计算图中每个节点的接近中心性。
* `nx.betweenness_centrality(G)`:计算图中每个节点的介数中心性。
**参数说明:**
* `G`:社交网络图。
* `component`:连通分量。
* `node`:连通分量中的节点。
# 4. 连通分量在图像处理中的应用
### 4.1 图像分割和目标识别
#### 4.1.1 图像分割的基本原理
图像分割是将图像分解成具有相似特征(如颜色、纹理、形状)的多个区域的过程。它在图像处理、目标识别和计算机视觉等领域有着广泛的应用。
#### 4.1.2 连通分量算法在图像分割中的应用
连通分量算法可以用于图像分割,通过识别图像中具有相同像素值的连通区域。具体步骤如下:
1. 将图像转换为二值图像,其中目标区域的像素值为 1,背景区域的像素值为 0。
2. 应用连通分量算法,将图像中的连通区域标记为不同的标签。
3. 根据标签将图像分割成不同的区域。
```python
import numpy as np
from skimage.measure import label
# 加载图像并转换为二值图像
image = np.array([[0, 0, 1, 1, 0],
[0, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 1, 1, 0]])
# 应用连通分量算法
labeled_image, num_objects = label(image, background=0)
# 根据标签分割图像
segmented_image = np.zeros_like(image)
for i in range(1, num_objects + 1):
segmented_image[labeled_image == i] = i
# 打印分割后的图像
print(segmented_image)
```
**代码逻辑分析:**
* `label` 函数将连通区域标记为不同的整数标签,背景区域标记为 0。
* `num_objects` 变量存储了连通区域的数量。
* 循环遍历标签,将每个连通区域的像素值设置为其标签值,从而实现图像分割。
### 4.2 图像连通性分析
#### 4.2.1 连通性度量的指标
图像连通性分析是评估图像中不同区域之间的连接程度的过程。常用的连通性度量指标包括:
* **连通区域数量:**图像中连通区域的数量。
* **最大连通区域面积:**图像中面积最大的连通区域的面积。
* **平均连通区域面积:**图像中所有连通区域面积的平均值。
* **连通性系数:**图像中所有像素属于连通区域的比例。
#### 4.2.2 连通分量算法在图像连通性分析中的应用
连通分量算法可以用于计算图像的连通性度量指标。具体步骤如下:
1. 应用连通分量算法,将图像中的连通区域标记为不同的标签。
2. 统计每个标签的像素数量,计算连通区域的数量和面积。
3. 计算连通性系数,即图像中属于连通区域的像素数量与图像中所有像素数量的比值。
```python
import numpy as np
from skimage.measure import label
# 加载图像
image = np.array([[0, 0, 1, 1, 0],
[0, 1, 1, 1, 0],
[1, 1, 1, 1, 1],
[1, 1, 1, 1, 1],
[0, 0, 1, 1, 0]])
# 应用连通分量算法
labeled_image, num_objects = label(image, background=0)
# 计算连通性度量指标
region_areas = []
for i in range(1, num_objects + 1):
region_areas.append(np.sum(labeled_image == i))
max_area = np.max(region_areas)
avg_area = np.mean(region_areas)
connectivity_ratio = np.sum(labeled_image > 0) / np.size(image)
# 打印连通性度量指标
print("连通区域数量:", num_objects)
print("最大连通区域面积:", max_area)
print("平均连通区域面积:", avg_area)
print("连通性系数:", connectivity_ratio)
```
**代码逻辑分析:**
* `label` 函数将连通区域标记为不同的整数标签,背景区域标记为 0。
* `num_objects` 变量存储了连通区域的数量。
* 循环遍历标签,计算每个连通区域的面积。
* 计算最大连通区域面积、平均连通区域面积和连通性系数。
# 5.1 物理学中的相变建模
### 5.1.1 相变的定义和特点
相变是指物质从一种相态转变为另一种相态的过程,例如固态到液态、液态到气态。相变通常伴随着物质性质的显著变化,如密度、体积、热容等。
### 5.1.2 连通分量算法在相变建模中的应用
连通分量算法在相变建模中主要用于识别和分析相变过程中形成的相域。相域是指相变过程中物质中具有相同相态的区域。通过连通分量算法,可以将相域识别为连通的子图,并分析其大小、形状和分布。
**应用示例:**
考虑一个固体材料的相变过程,其中固体从一个单一的相态转变为两个不同的相态。使用连通分量算法,可以识别和分析形成的两个相域,并研究其随时间变化的规律。
```python
import numpy as np
from scipy.ndimage import label
# 模拟相变过程,生成二值图像
image = np.random.rand(100, 100) > 0.5
# 使用连通分量算法识别相域
labeled_image, num_components = label(image)
# 分析相域的大小和形状
component_sizes = np.bincount(labeled_image.flatten())
component_shapes = [np.unique(labeled_image[labeled_image == i]).size for i in range(1, num_components + 1)]
# 输出结果
print("Number of components:", num_components)
print("Component sizes:", component_sizes)
print("Component shapes:", component_shapes)
```
**代码逻辑分析:**
* `label()`函数使用连通分量算法对图像进行标记,并返回标记后的图像和连通分量数。
* `np.bincount()`函数统计每个连通分量中像素的个数,即相域的大小。
* `np.unique()`函数统计每个连通分量中唯一像素值的个数,即相域的形状。
连通分量算法在相变建模中提供了强大的工具,可以帮助研究人员分析相变过程中的相域演化规律,为理解相变机制和预测材料性能提供重要信息。
# 6. 连通分量算法的优化和拓展
### 6.1 算法优化技术
#### 6.1.1 并行化算法
并行化算法通过将连通分量算法分解成多个独立的任务,并行执行这些任务,从而提高算法的效率。
**实现细节:**
- 将图中的顶点分配到不同的处理单元上。
- 每个处理单元独立执行连通分量算法,计算其分配到的顶点的连通分量。
- 最后,将各个处理单元的结果合并,得到图中所有顶点的连通分量。
#### 6.1.2 启发式算法
启发式算法通过使用启发式规则来指导算法的搜索过程,从而减少算法的时间复杂度。
**实现细节:**
- **基于大小的启发式算法:**优先探索规模较大的连通分量,因为它们更容易被发现。
- **基于密度的启发式算法:**优先探索密度较大的区域,因为它们更有可能包含连通分量。
### 6.2 算法拓展
#### 6.2.1 加权连通分量算法
加权连通分量算法考虑了图中边的权重,并计算具有最大权重和的连通分量。
**实现细节:**
- 在执行连通分量算法时,将边的权重作为参数传递。
- 在合并连通分量时,选择具有最大权重和的连通分量。
#### 6.2.2 动态连通分量算法
动态连通分量算法可以处理图中动态变化,例如顶点的添加或删除。
**实现细节:**
- 使用数据结构(例如并查集)来维护连通分量。
- 当图发生变化时,更新数据结构以反映这些变化。
0
0





