图论进阶：连通分量的优化算法与复杂度分析，揭开算法背后的秘密

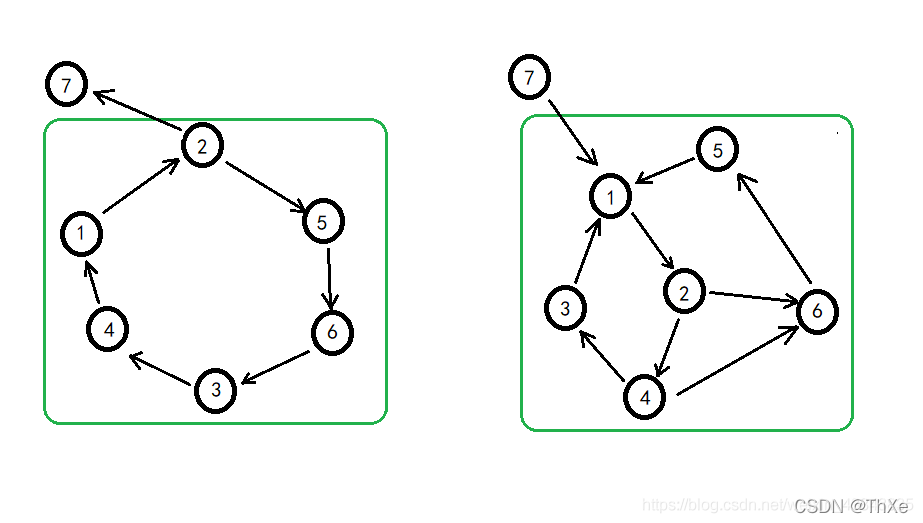
# 1. 图论基础与连通分量概念

**1.1 图论基础**

图论是研究图结构及其性质的数学分支。图由顶点和边组成，其中顶点表示实体，边表示实体之间的关系。图论在计算机科学、网络分析和运筹学等领域有着广泛的应用。

**1.2 连通分量概念**

连通分量是一个图中的一组顶点，这些顶点可以通过路径相互到达。连通分量是图论中一个重要的概念，它可以用来分析图的连通性、识别图中的社区或簇，以及解决各种优化问题。

# 2. 连通分量的优化算法

在图论中，连通分量是一个重要的概念，它代表了图中相互连接的顶点集合。寻找连通分量是图论中一项基本的任务，在许多实际应用中都有着广泛的应用。为了提高连通分量的寻找效率，研究人员提出了多种优化算法，包括深度优先搜索（DFS）、广度优先搜索（BFS）和并查集算法。

### 2.1 深度优先搜索（DFS）算法

#### 2.1.1 DFS算法的基本原理

深度优先搜索（DFS）算法是一种递归算法，它从图中的一个顶点开始，沿着一条路径一直向下探索，直到无法再向下探索为止。然后，它回溯到上一个顶点，沿着另一条路径继续探索。这个过程重复进行，直到图中所有顶点都被访问过。

DFS算法的基本原理可以用以下步骤描述：

1. 从图中的一个顶点开始，标记它为已访问。
2. 访问该顶点的所有未访问的邻接顶点。
3. 对每个邻接顶点，重复步骤1和2。
4. 如果没有未访问的邻接顶点，则回溯到上一个顶点。
5. 重复步骤1-4，直到图中所有顶点都被访问过。

#### 2.1.2 DFS算法的实现和复杂度分析

DFS算法可以用递归或非递归的方式实现。以下是一个递归实现的伪代码：

def dfs(graph, start):
    visited.add(start)
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor)

DFS算法的时间复杂度为O(V + E)，其中V是图中顶点的数量，E是图中边的数量。这是因为DFS算法需要访问每个顶点和每条边一次。

### 2.2 广度优先搜索（BFS）算法

#### 2.2.1 BFS算法的基本原理

广度优先搜索（BFS）算法是一种层次遍历算法，它从图中的一个顶点开始，先访问该顶点的所有邻接顶点，然后再访问这些邻接顶点的邻接顶点，以此类推。这个过程一直持续到图中所有顶点都被访问过。

BFS算法的基本原理可以用以下步骤描述：

1. 从图中的一个顶点开始，将其加入一个队列中。
2. 从队列中取出一个顶点，并标记它为已访问。
3. 访问该顶点的所有未访问的邻接顶点，并将其加入队列中。
4. 重复步骤2和3，直到队列为空。

#### 2.2.2 BFS算法的实现和复杂度分析

BFS算法可以用队列实现。以下是一个伪代码实现：

def bfs(graph, start):
    queue = [start]
    visited.add(start)
    while queue:
        current = queue.pop(0)
        for neighbor in graph[current]:
            if neighbor not in visited:
                queue.append(neighbor)
                visited.add(neighbor)

BFS算法的时间复杂度也为O(V + E)，与DFS算法相同。这是因为BFS算法也需要访问每个顶点和每条边一次。

### 2.3 并查集算法

#### 2.3.1 并查集算法的基本原理

并查集算法是一种数据结构，它用于维护一组不相交的集合。并查集算法支持以下操作：

* 查找：查找一个顶点所属的集合。
* 合并：合并两个集合。

并查集算法的基本原理是使用一个数组来存储每个顶点所属的集合。数组中的每个元素要么是该顶点本身（表示该顶点是一个集合的代表），要么是该顶点所属集合的代表。

#### 2.3.2 并查集算法的实现和复杂度分析

并查集算法可以用以下伪代码实现：

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]
        self.size = [1 for i in range(n)]

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        x_root = self.find(x)
        y_root = self.find(y)
        if x_root != y_root:
            if self.size[x_root] < self.size[y_root]: