opencv中的形态学图像处理技术介绍

# 1. 图像处理基础概念

### 1.1 数字图像的基本原理
在图像处理中，数字图像以矩阵形式表示，每个元素称为像素。像素的颜色由RGB值或灰度值表示。RGB值包含红、绿、蓝三个通道的强度，灰度图像则只有一个通道表示亮度。

### 1.2 图像处理的基本操作
图像处理涉及读取、显示和存储图像。通过编程实现图像的读取、处理和保存，能够实现许多有趣的功能，比如图像增强、特征提取等。同时，程序员还可以利用图像库对图像进行各种操作。

数字图像处理是一个广泛的领域，掌握图像的基本原理和操作对于进一步学习图像处理技术至关重要。在实际应用中，图像处理技术被广泛应用于医学影像、计算机视觉、数字媒体等领域。

# 2.1 形态学概念基础
形态学图像处理是一种基于结构元素的图像处理方法，主要应用于图像的形态学特征提取和图像分割。在这一章节中，我们将深入探讨形态学的基础概念，包括结构元素的概念与作用、膨胀和腐蚀操作介绍以及开运算与闭运算的意义。

### 2.1.1 结构元素的概念与作用
结构元素是形态学处理中的重要概念，它定义了一种形状和大小，用于对图像进行局部操作。结构元素可以是各种形状，如矩形、圆形等。在形态学处理中，结构元素与图像进行滑动匹配，通过与像素进行比较来改变像素值，从而实现图像的各种处理操作。

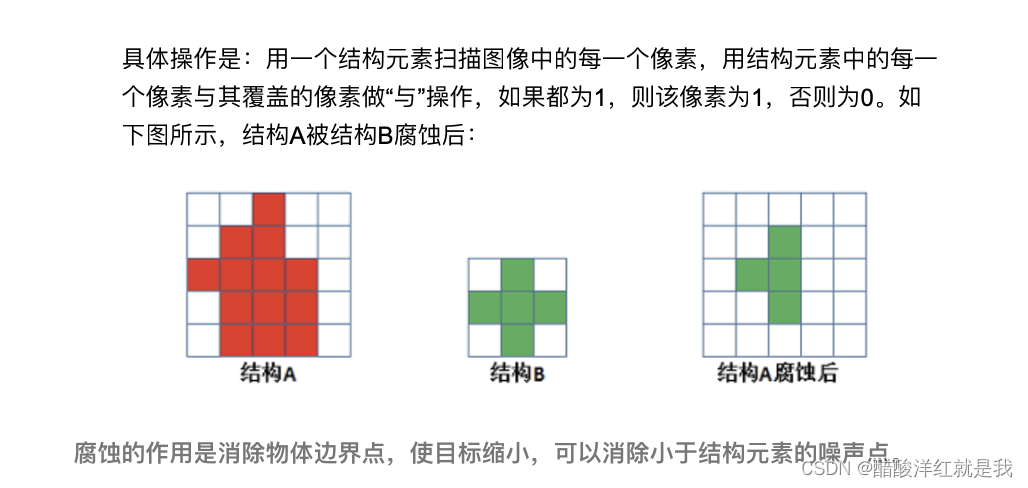
### 2.1.2 膨胀和腐蚀操作介绍
膨胀（Dilation）和腐蚀（Erosion）是形态学处理中最基本的操作之一。膨胀操作可以使图像中的物体边界膨胀，填充物体之间的空隙，常用于连接断开的物体或填充小的空洞；而腐蚀操作则可以使图像中的物体边界向内收缩，去除物体之间的小连接。

### 2.1.3 开运算与闭运算的意义
开运算（Opening）和闭运算（Closing）是形态学处理中基于膨胀和腐蚀操作组合而成的两种操作。开运算先进行腐蚀后进行膨胀，可用于去除小型噪点；闭运算先进行膨胀后进行腐蚀，可用于填充物体内部的小洞。这两种操作常常结合使用，能够有效平滑图像并保留物体的整体形状。

## 2.2 形态学滤波技术
形态学滤波是一种基于形态学理论的图像处理方法，主要用于去除图像中的噪声、增强边缘以及检测图像中的特定模式。在这一节中，我们将探讨形态学梯度的应用、礼帽运算与黑帽运算以及顶帽运算的使用案例。

### 2.2.1 形态学梯度的应用
形态学梯度是通过对图像进行膨胀和腐蚀操作后取差集得到的图像，主要用于检测图像的边缘。形态学梯度可以帮助我们找到图像中物体的边界，并在一定程度上增强图像的边缘信息，常用于图像分割和特征提取。

### 2.2.2 礼帽运算与黑帽运算
礼帽运算（Top Hat）和黑帽运算（Black Hat）是形态学滤波中常用的操作。礼帽运算可以帮助我们提取图像中的小型明亮区域，而黑帽运算则可以提取图像中的小型暗区域。这两种运算通常用于增强图像的局部对比度和特定区域的特征。

### 2.2.3 顶帽运算的使用案例
顶帽运算（Top-Hat）是指原始图像与进行开运算后得到的图像进行差运算得到的图像，主要用于提取图像中的小尺度亮区域。顶帽运算在图像增强和特征提取中有着广泛的应用，能够帮助我们发现图像中细微的特征，并突出图像的亮部细节。

# 3. 形态学图像处理进阶

### 3.1 形态学轮廓检测
形态学轮廓检测是图像处理中的重要任务之一，通过检测图像中的边缘信息来描述目标对象的形状和结构。形态学运算在轮廓检测中扮演着重要的角色，可以有效提取出目标物体的外形信息。

#### 3.1.1 外轮廓与内轮廓的区别
外轮廓是指目标物体的外部边缘轮廓，而内轮廓则是目标物体内部的边缘轮廓。外轮廓常用于目标检测和分割，而内轮廓则用于检测目标内部的孔洞等特征。

#### 3.1.2 检测图像中的孔洞
在图像处理中，孔洞是指目标内部的空洞区域，通常需要检测和填充以完整描述目标的形状。形态学运算中的闭运算可以帮助填充孔洞，使目标边缘更加完整准确。

#### 3.1.3 轮廓拟合与提取技术
轮廓拟合是指利用数学模型拟合目标轮廓，常用的拟合方法包括最小二乘拟合、Bezier 曲线拟合等。轮廓提取技术则是从图像中提取出目标的边缘信息，常用的算法有Canny 边缘检测、Sobel 算子等。

### 3.2 形态学形状分析
形态学形状分析是利用形态学方法对图像中目标的形状特征进行提取和分析的过程，可以帮助理解目标的几何结构和形态特征，进而实现更深