【性能对比】：原补码除法与其他算术运算的效率分析（选择最佳的计算策略）


# 摘要
本文系统地探讨了原补码除法的基础理论和性能分析，通过对比原补码除法与其他算术运算，深入阐释了其在不同场景中的应用及性能表现。文中首先详细介绍了补码与原码的概念、特性以及原补码除法的算法原理和数学模型。接着，文章着重于原补码除法的实践应用，包括程序设计、边界条件处理，以及性能测试方法的探讨。此外，本文提出了根据性能需求选择最佳算术运算策略的方法，并通过案例研究探讨了如何优化特定计算场景下的性能。最后，文章总结了原补码除法的研究结论，并展望了未来算术运算的研究方向，如量子计算和人工智能在该领域的影响和应用前景。

# 关键字
原补码除法；补码与原码；算法原理；性能测试；计算策略优化；量子计算

参考资源链接：[原补码除法详解：恢复余数与加减交替法](https://wenku.csdn.net/doc/33ma07vp9s?spm=1055.2635.3001.10343)
# 1. 原补码除法基础与性能分析概述

## 1.1 原补码除法概念简述
原补码除法是计算机算术中的一种重要技术，尤其在处理整数运算时表现出色。它通过特定的编码方式（原码和补码）实现数学上的除法操作，这在各种硬件和软件应用中都有广泛运用。

## 1.2 性能分析的重要性
了解原补码除法的基础后，进行性能分析是非常关键的。性能分析不仅帮助我们理解其运算效率，还能通过比较不同算法找到最佳实现路径，进而提升整体计算性能和资源利用率。

## 1.3 本章结构概述
本章将介绍原补码除法的基本概念及其在性能分析方面的应用。我们将深入探讨它在计算机硬件与软件中如何工作，以及在不同场景下的性能表现。通过对性能测试和优化策略的学习，为后续章节中更深层次的探讨打下基础。

# 2. 原补码除法的理论基础

原补码除法是计算机算术运算的一个基础领域，在现代计算机体系结构中扮演着关键角色。在深入讨论其应用和性能测试之前，我们首先需要理解它的理论基础，这包括补码与原码的基本概念、原补码除法的算法原理，以及其在不同算术运算中的应用。

## 2.1 补码与原码的基本概念

### 2.1.1 补码的定义和特性

在计算机系统中，整数通常使用补码（Two's complement）形式表示。补码的最大优势在于简化了加法和减法运算的硬件实现，特别是对于二进制运算。补码的定义基于一个简单的规则：一个数的补码等于其反码加1。补码的一个重要特性是，它将表示零的唯一性简化为一个单一的值（即0），这在二进制加法和减法中提供了便利。

例如，对于一个4位的二进制系统，`+3`的表示如下：
- 原码：`0011`
- 反码：`1100`
- 补码：`1101`（反码加1）

反观`-3`的表示：
- 原码：`1001`
- 反码：`1110`
- 补码：`1111`（反码加1）

### 2.1.2 原码的定义和特性

原码是一种直接表示法，它是将一个数字的绝对值的二进制形式直接表示出来，并在最前面加上符号位（通常0表示正，1表示负）。虽然原码直观，但在计算机运算中，尤其是在二进制加减法中，原码存在一些不便之处。例如，加减混合运算需要额外的逻辑来处理符号位。

在同样的4位二进制系统中，`+3`和`-3`的原码表示分别为：
- `+3`：`0011`
- `-3`：`1011`

由于原码的表示方式使得加法和减法需要复杂的逻辑，所以计算机在进行二进制运算时，通常会将负数转换为补码形式进行。

## 2.2 原补码除法的算法原理

### 2.2.1 除法算法的基本步骤

原补码除法本质上是一种迭代算法，它通过反复的加法和减法操作来逼近商。这种算法的核心在于不断调整余数和减去除数，直到余数小于除数，此时余数即为最终的余数。

在手动执行除法时，我们会执行类似以下步骤：
1. 将被除数的二进制位与除数的最高有效位对齐。
2. 如果被除数的当前部分大于等于除数，则从被除数中减去除数，并将商的相应位置为1。
3. 将被除数左移一位，重复步骤2，直到被除数的每一位都被检查。
4. 商的最终值就是经过上述步骤计算得到的值。

### 2.2.2 原补码除法的数学模型

原补码除法的数学模型可以表述为：

假设我们有两个整数`A`和`B`（`A`是被除数，`B`是除数），我们想要计算`A`除以`B`的商`Q`和余数`R`。数学模型可以表示为：

A = B * Q + R

其中`Q`和`R`都应该是整数，且`R`的绝对值小于`B`的绝对值。在补码运算中，如果`A`是负数，除法的结果将根据补码的规则来计算。

## 2.3 原补码除法与其他算术运算的对比

### 2.3.1 整数运算与浮点运算的区别

整数运算通常涉及到原码和补码的直接操作，而浮点运算则使用IEEE标准的表示法。两种运算在处理数值的范围和精度上有明显差异。整数运算简单且执行速度快，但不能表示小数点后的数；而浮点运算能够表示非常小和非常大的数，但代价是复杂性增加，且在某些情况下可能存在精度损失。

### 2.3.2 原补码除法在不同运算中的位置

在进行算术运算时，原补码除法与其他运算如乘法、加法等存在互补关系。例如，在执行一些复杂的算法时，除法运算可能需要与乘法运算配合使用，如在执行多项式展开的运算时。在这些场景中，理解原补码除法的原理对于编写正确且高效的算法至关重要。

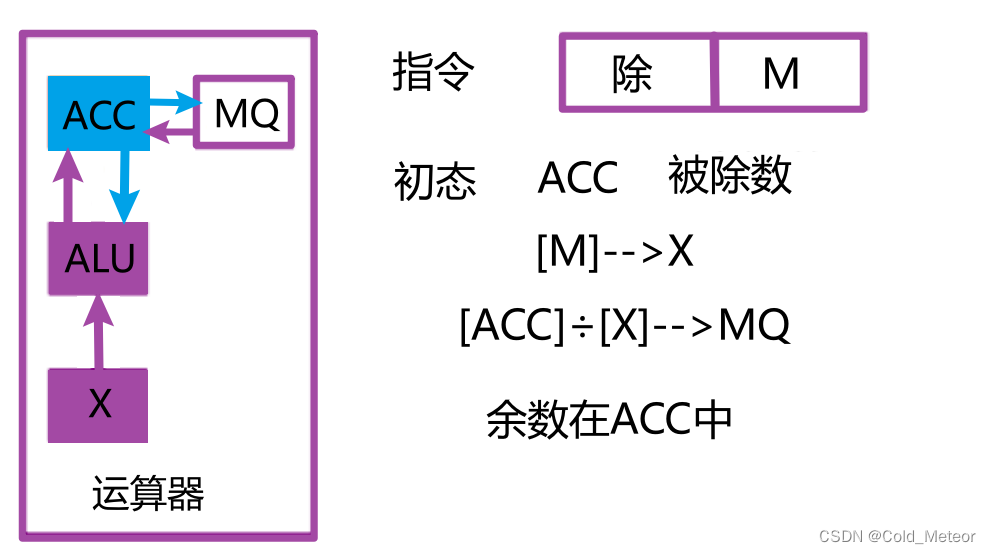
在现代的计算机系统中，原补码除法作为基本算术操作的一部分，通常是由CPU内置的算术逻辑单元（ALU）直接支持的。因此，从性能角度出发，利用原生指令执行除法运算通常比软件模拟的方法更高效。在实际应用中，开发者可以利用这些原生指令来优化程序性能。

# 3. 原补码除法的实践应用与性能测试

## 3.1 实现原补码除法的程序设计

### 3.1.1 编写原补码除法的代码框架

在本章节中，我们将具体介绍如何使用编程语言实现原补码除法的代码框架。以 C 语言为例，原补码除法