【浮点数运算】：原补码除法在现代编程中的高级应用（浮点数运算的隐藏技巧）


# 摘要
本文详细探讨了浮点数运算的基础理论与实践应用。首先，介绍了浮点数运算的基本概念和原补码表示法，并阐述了其在除法中的应用原理。接着，深入分析了浮点数加减乘除的数学原理，重点讨论了IEEE标准下的浮点数表示和基本算法。在编程实现方面，文章探讨了二进制除法的手动实现技巧以及现代编程语言中浮点数运算的内置支持和性能考量。此外，本文还深入探讨了浮点数运算的优化和高级技巧，包括精度控制、舍入策略、向量化和并行计算的应用。最后，通过实际应用案例分析，展示了浮点数运算在科学计算和工程领域的关键作用，并提供了相应的优化策略。

# 关键字
浮点数运算；原补码表示法；IEEE标准；精度控制；数值算法；并行计算

参考资源链接：[原补码除法详解：恢复余数与加减交替法](https://wenku.csdn.net/doc/33ma07vp9s?spm=1055.2635.3001.10343)
# 1. 浮点数运算基础概念

浮点数运算是计算机科学中的核心概念之一，尤其在处理大量连续数据的科学计算和工程应用中显得尤为重要。理解浮点数运算，首先要从它的基础概念入手。浮点数由两部分组成：尾数（mantissa）和指数（exponent）。这种结构使浮点数能够表示非常大或非常小的数。浮点数的关键特性是它的动态范围，这意味着它可以在保持精度的同时，覆盖广泛的不同数值大小。浮点数运算要遵循特定的数学规则和计算机标准，如IEEE 754标准，它定义了浮点数的存储和运算方式。在接下来的章节中，我们将深入探讨原补码表示法以及浮点数运算的理论和实践应用，揭示其在编程实现中的操作技巧和性能优化方法。

# 2. ```
# 第二章：原补码除法的理论基础

## 2.1 原补码表示法简述

### 2.1.1 二进制补码的概念
补码是一种用于表示有符号数的方法，它允许加法和减法使用相同的硬件电路。在补码系统中，正数和零的表示与其在无符号二进制系统中的表示相同，而负数则以它们正数对应值的二进制表示的补码形式表示。计算一个数的补码可以通过按位取反（即1变0，0变1）然后加1来完成。例如，-3的补码表示是通过取+3的二进制表示（0011），按位取反（1100），再加1得到（1101）。

### 2.1.2 原补码在除法中的应用原理
在计算机中进行除法运算时，尤其是涉及到有符号数的除法时，通常会依赖于补码来简化运算。原码表示法直接使用二进制的正常形式来表示负数，即最高位为符号位。在进行除法运算时，将被除数和除数转换为相同符号的补码形式，然后执行无符号二进制除法操作，最后将结果的符号位单独处理。由于除法运算本质上是重复的减法和移位操作，补码表示法使得这些操作可以在硬件级别上高效实现。

## 2.2 浮点数运算的数学原理

### 2.2.1 IEEE标准下的浮点数表示
IEEE 754标准定义了浮点数在计算机中的存储方式，它将浮点数分成三个部分：符号位、指数部分和尾数部分。符号位确定数值的正负，指数部分表示数值的范围，尾数部分则提供数值的精度。浮点数的精确值由下面的公式计算得出：

\[ (-1)^{符号位} \times (1.尾数部分) \times 2^{(指数部分 - 偏移量)} \]

其中，偏移量是一个根据指数位宽选择的特定值，目的是使指数以二进制补码形式存储时能够表示正数和负数。

### 2.2.2 浮点数加减乘除的基本算法
浮点数的加减乘除算法比整数复杂得多，因为需要对阶、尾数运算和规格化。以加法为例，需要将两个浮点数的指数部分对齐，即将较小的指数增加，直到与较大的指数相等。然后将指数相等的两个尾数进行相加，并进行规格化处理。乘法运算相对简单，只需将两个数的指数部分相加，尾数部分进行二进制乘法运算，再进行适当的规格化和舍入处理。除法和乘法类似，只是将乘法转换为除法，将一个尾数除以另一个尾数，并处理结果的规格化和舍入。

以上内容为第二章的概览，接下来将详细展开介绍原补码在除法中的应用原理，以及IEEE标准下的浮点数表示和基本算法。

### 二进制补码在除法中的应用

在计算机中执行除法时，尤其是在涉及到有符号数时，补码表示法让复杂的操作变得简单。补码的好处之一在于它能够使用同样的电路来执行加法和减法操作。这种便利性源自补码的定义，即一个数的负数表示为其补码。例如，对于有符号的整数-12，在8位二进制中可以表示为补码：11110100。

为了执行一个除法操作，计算机系统将首先转换任何有符号操作数到其补码等效形式。例如，如果需要执行 -12 / 4，计算机首先会找到 -12 的补码（如上所示），然后将这个补码与 4 的二进制等效形式进行操作。因为除法涉及到多次减法操作（直到余数不足以减去除数），补码表示法允许每次减法操作后不需要重新编码。

现在，考虑一个实际的除法操作。如果我们要执行 10 / 3，可以按照以下步骤手工实现：

1. 将被除数和除数转换为二进制：10(十进制) = 1010(二进制)，3(十进制) = 0011(二进制)。
2. 通过适当的左移操作对齐它们的位，使得除数的位数与被除数的位数相同。
3. 将被除数的尾数部分（在这个例子中，尾数就是被除数本身）与除数进行比较。
4. 在满足条件的位上，执行减法操作，并记录结果。
5. 重复以上步骤，将余数左移，比较，并执行减法操作，直到得到最终结果。

### IEEE标准下的浮点数表示

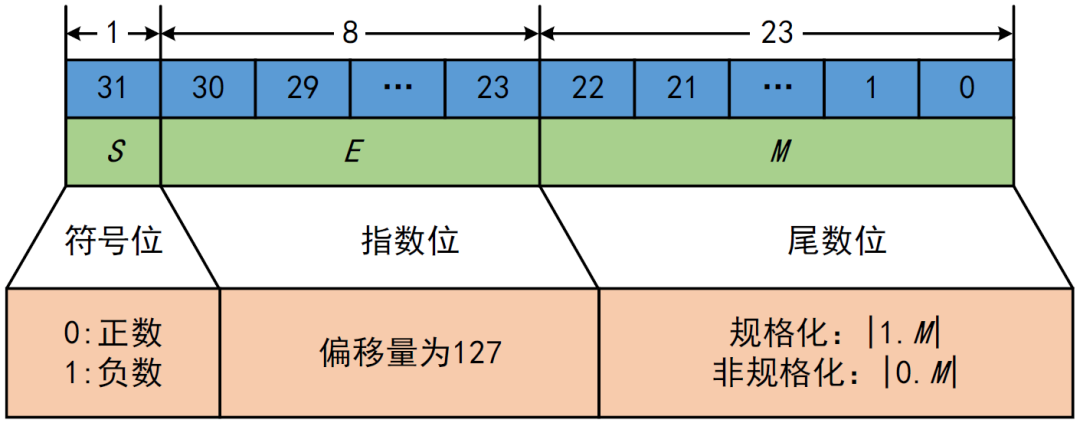
IEEE 754标准是广泛使用的浮点数运算标准，它定义了32位（单精度）和64位（双精度）浮点数的格式。在这些格式中，每个浮点数由三个主要部分构成：符号位（sign）、指数位（exponent）和尾数位（mantissa，也被称作分数部分或有效数字）。对于单精度浮点数，1位用于符号，8位用于指数，23位用于尾数；双精度浮点数分别占用1位、11位和52位。

符号位表示数字的正负，0为正数，1为负数。指数部分用于表示浮点数的范围，而尾数部分则表示在二进制小数点后的有效数字。指数位不是直接存储实际指数值，而是存储指数与偏移值的和，这个偏移值是为了让指数部分能够表示正负指数。在32位浮点数中，这个偏移量是127；在64位中是1023。

举例来说，如果我们有一个32位的IEEE 754表示的浮点数1.01011 x 2^1，转换为二进制形式后，符号位是0（表示正数），指数部分是129（二进制表示为10000001），加上偏移值127得到实际指数值，尾数部分为01