DFS 算法在图论中的应用及效果分析

# 1. 图论基础知识

在计算机科学领域，图论是一门重要的研究领域，用于描述和解决各种实际问题。图由节点和边组成，其中节点表示实体，边表示节点之间的关系。常见的图论术语包括有向图（边有方向性）和无向图（边无方向性），以及加权图（边带有权重）和非加权图（边没有权重）。有向图用于模拟网络拓扑结构，而加权图适用于路由最短路径等问题的求解。理解这些基本概念对于学习和应用图论算法至关重要。通过分类学习，我们能够更深入地理解图的特性和应用场景。

# 2. DFS 算法基本原理

DFS 是图论中一种常用的算法，其原理是以深度优先的方式遍历图的各个节点，通过不断深入直到无法再深入为止。DFS 算法可以采用递归或栈来实现，下面将详细介绍其基本原理及实现方式。

#### DFS 算法概述

DFS 算法即深度优先搜索算法，其核心思想是从起始节点开始，尽可能深的搜索图的分支。DFS 算法一般用于解决图的遍历和路径搜索问题。在遍历过程中，每个节点都会被标记为“已访问”，以避免重复访问。

##### 递归方式深度优先遍历

递归方式是 DFS 算法最直观的实现方式，通过函数的递归调用来遍历图的各个节点。具体实现时，首先访问当前节点，然后递归访问当前节点的邻居节点，直到遍历完整个图。

def dfs_recursive(node, visited):
    if node not in visited:
        visited.add(node)
        for neighbor in graph[node]:
            dfs_recursive(neighbor, visited)

##### 栈方式深度优先遍历

除了递归方式，DFS 还可以通过显式地使用栈来实现。通过不断将当前节点的邻居节点入栈，再出栈进行访问，直到栈为空为止。这种实现方式也能有效避免递归调用带来的栈溢出问题。

def dfs_stack(start_node):
    stack = [start_node]
    visited = set()
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            for neighbor in graph[node]:
                if neighbor not in visited:
                    stack.append(neighbor)

#### DFS 实现

DFS 算法的实现需要根据具体情况选择适合的方式，下面对其伪代码进行详细解析，同时通过图示演示来更直观地理解算法的执行过程。

##### 伪代码解析

DFS 算法的伪代码可以描述为从起始节点开始，依次访问其未访问过的邻居节点，直到遍历完整个图的过程。在实现时需要注意节点访问标记，以防止重复访问。

def dfs(node, visited):
    if node not in visited:
        visited.add(node)
        for neighbor in graph[node]:
            dfs(neighbor, visited)

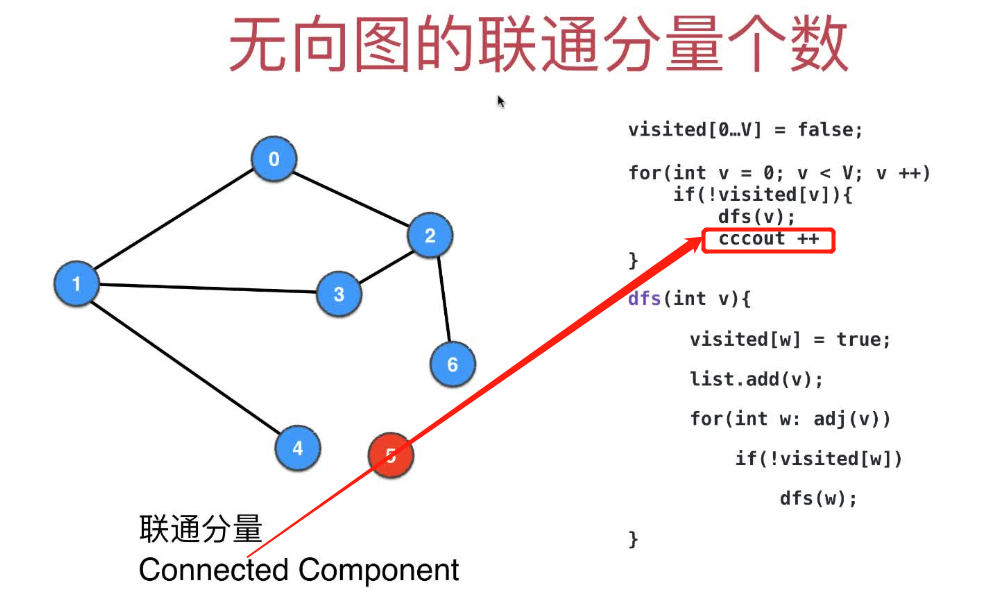
##### 图示演示

下面通过一个简单的图示来演示 DFS 算法的执行过程。假