DFS 算法如何处理图数据结构中的环路检测问题

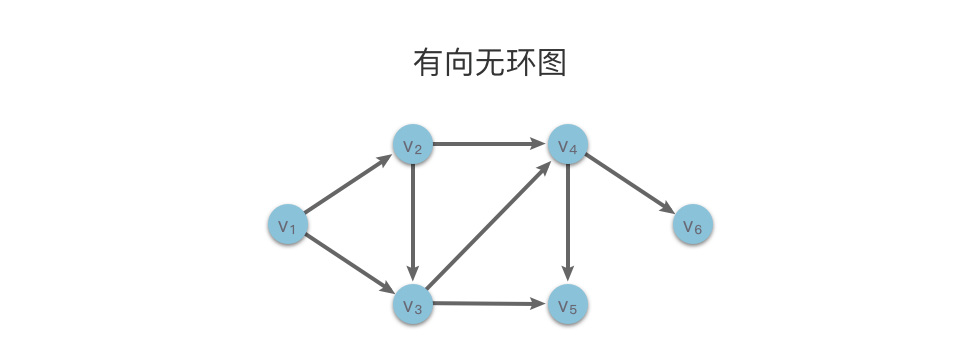
# 1. 图数据结构简介

图是一种非常重要的数据结构，用来描述元素之间的关系。在图论中，图被用来表示各种实物之间的连接关系，比如交通网络、社交网络等。图可以分为无向图和有向图，其中无向图的边没有方向性，而有向图的边带有箭头表示方向。图可以用邻接矩阵、邻接表或关联矩阵等方式表示，每种表示方法有其适用的场景和特点。邻接矩阵适合稠密图，邻接表适合稀疏图，而关联矩阵则可以表示有向图和无向图的关系。深入理解图数据结构对于后续探讨图算法以及解决实际问题具有重要意义。

# 2. 常见图算法初探
- **2.1 深度优先搜索（DFS）算法**
- 2.1.1 基本原理
深度优先搜索（Depth First Search，DFS）是一种用于遍历或搜索树或图的算法。其基本原理是尽可能深地搜索图的分支，直到这条路走到底，然后再回溯前一节点，尝试探索下一个分支。

- 2.1.2 递归实现

DFS的递归实现是最直观的方法之一。通过递归调用，可以依次访问图中的所有节点，并标记已访问的节点，避免重复访问。

def dfs_recursive(graph, start, visited):
    if start not in visited:
        visited.add(start)
        print(start)
        for neighbor in graph[start]:
            dfs_recursive(graph, neighbor, visited)

- 2.1.3 迭代实现

迭代实现的DFS常使用栈来辅助实现，通过不断将节点压入栈并弹出栈顶节点来完成遍历过程。

def dfs_iterative(graph, start):
    visited = set()
    stack = [start]
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.add(node)
            print(node)
            stack.extend([neighbor for neighbor in graph[node] if neighbor not in visited])

- **2.2 广度优先搜索（BFS）算法**
- 2.2.1 基本原理

广度优先搜索（Breadth First Search，BFS）是另一种常用的图搜索算法，它从起始节点开始，逐层遍历图中的节点，直到找到目标节点为止。

- 2.2.2 实现方法

BFS一般使用队列来实现，通过不断将节点加入队列并弹出队首节点的方式来完成广度优先搜索。

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    while queue:
        node = queue.popleft()
        if node not in visited:
            visited.add(node)
            print(node)
            queue.extend([neighbor for neighbor in graph[node] if neighbor not in visited])

- 2.2.3 应用场景

BFS常用于寻找图中节点之间的最短路径问题，例如在迷宫求解、社交网络中查找好友关系等场景中被广泛应用。

# 3. 环路检测算法思路概述
#### 3.1 环路检测问题的定义
环路是指图中至少有一条边使得一个顶点通过该边回到自身，形成闭合的路径。环路检测是在图中判断是否存在这样的路径的问题。环路检测在很多领域有重要应用，如网络路由算法、数据库的事务处理等。

#### 3.1.1 什么是图中的环路
在无向图中，如果存在一条从顶点 A 到顶点 B 的路径，使得 A 不等于 B，且这条路径中没有重复的顶点，则称这条路径为一个环路。在有向图中，若存