时间复杂度优化技巧：提升算法效率，优化代码性能

# 1. 算法时间复杂度的基础概念

时间复杂度是衡量算法效率的重要指标，它描述了算法执行所需要的时间。算法的时间复杂度通常用大 O 符号表示，例如 O(n)、O(n^2) 和 O(log n)。

* **大 O 符号：**大 O 符号表示算法在最坏情况下所需的时间。它忽略常数因子和低阶项。例如，O(n) 表示算法在最坏情况下需要与输入大小 n 成正比的时间。
* **输入大小：**算法的时间复杂度通常与输入大小有关。输入大小通常用 n 表示，它表示输入中元素的数量或数据的长度。

# 2. 优化算法时间复杂度的理论基础

### 2.1 时间复杂度的度量标准

时间复杂度是衡量算法效率的一个重要指标，它描述了算法执行时间与输入规模之间的关系。常用的时间复杂度度量标准有：

* **最坏情况时间复杂度 (Worst-Case Time Complexity)**：表示算法在最不利情况下执行所需的时间。
* **平均情况时间复杂度 (Average-Case Time Complexity)**：表示算法在所有可能输入上的平均执行时间。
* **最好情况时间复杂度 (Best-Case Time Complexity)**：表示算法在最有利情况下执行所需的时间。

### 2.2 常见的时间复杂度类型

常见的时间复杂度类型包括：

| 时间复杂度 | 符号表示 | 描述 |
|---|---|---|
| 常数时间复杂度 | O(1) | 算法执行时间与输入规模无关 |
| 线性时间复杂度 | O(n) | 算法执行时间与输入规模 n 成正比 |
| 对数时间复杂度 | O(log n) | 算法执行时间与输入规模 n 的对数成正比 |
| 平方时间复杂度 | O(n²) | 算法执行时间与输入规模 n 的平方成正比 |
| 指数时间复杂度 | O(2ⁿ) | 算法执行时间随着输入规模 n 的增加呈指数增长 |

### 2.3 时间复杂度的分析方法

分析算法的时间复杂度通常使用以下方法：

* **渐近分析法**：忽略常数项和低阶项，只关注算法执行时间的主导项。
* **主定理**：用于分析具有递归结构的算法的时间复杂度。
* **经验分析**：通过实际运行算法来测量其执行时间。

**代码块：**

def factorial(n):
    if n == 0:
        return 1
    else:
        return n * factorial(n-1)

**逻辑分析：**

该代码块计算 n 的阶乘。递归调用将导致算法执行时间呈指数增长，因此其时间复杂度为 O(2ⁿ)。

**参数说明：**

* `n`：要计算阶乘的整数

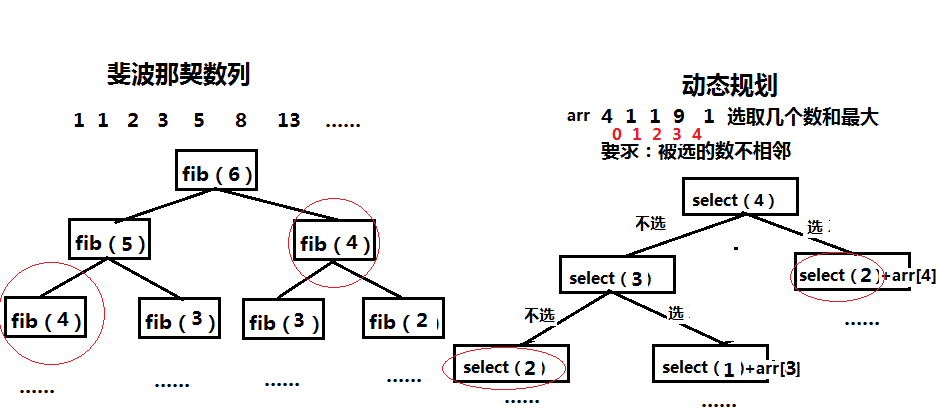
# 3.1 减少不必要的计算

#### 3.1.1 避免重复计算

重复计算是指在算法中多次计算相同的值，这会浪费大量的时间。避免重复计算的方法有：

- **使用中间变量存储计算结果：**将中间计算结果存储在变量中，避免重复计算。例如：

# 计算斐波那契数列的第 n 项
def fibonacci(n):
    if n == 0: