【深度学习基础必备】：神经网络模型优化的先修课程

# 1. 深度学习基础概念

深度学习是机器学习的一个子领域，它利用多层神经网络来学习数据的高级抽象表示。这一领域自2006年被提出以来，已经在语音识别、图像处理、自然语言理解等多个领域取得了显著的成就。深度学习通过学习数据的层次结构，使得计算机能够自动发现数据中的特征，从而减少了人工特征工程的需求。

在深入探讨神经网络的数学原理和模型结构之前，理解深度学习的基础概念是至关重要的。本章将带领读者对深度学习的基本概念进行梳理，包括神经网络的定义、类型以及学习过程中的核心思想。我们会先从神经元和网络的基本单元开始，逐步建立起对深度学习框架的初步认识。

graph LR
A[深度学习基础] --> B[神经网络定义]
B --> C[学习过程]
C --> D[类型与应用]

接下来，我们将详细介绍神经网络的基本单元——神经元，以及如何通过层与层之间的连接形成网络结构。此外，我们还会探讨神经网络在学习过程中是如何通过反向传播算法调整权重，以及如何优化网络结构以适应各种不同类型的复杂任务。通过本章的介绍，读者将对深度学习有一个全面而基础的理解，为后续章节中神经网络的深入学习打下坚实的基础。

# 2. 神经网络的数学基础

### 2.1 线性代数在神经网络中的应用
在深度学习中，线性代数是一个不可或缺的基础数学领域。几乎所有的数据在计算机中的表示和处理，都离不开线性代数的概念和运算。本小节将深入讨论矩阵运算与张量操作，以及微分与梯度下降法，这些构成了神经网络的核心数学基础。

#### 2.1.1 矩阵运算与张量操作
矩阵运算是一种极其重要的数学工具，在神经网络中，数据、参数和中间输出经常以矩阵形式表示。矩阵运算包括加法、乘法、转置、求迹、求逆等，这些操作可以用于实现线性变换、点积和权重更新等关键步骤。

一个典型的矩阵乘法示例如下：

import numpy as np

# 定义两个矩阵 A 和 B
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 执行矩阵乘法 C = A * B
C = np.dot(A, B)

矩阵乘法在神经网络中往往对应于前向传播时的线性变换。每个矩阵可以被解释为数据集中的一个批次，其中行代表样本，列代表特征。每个神经元的线性组合可以用矩阵乘法来表示，这大大提高了计算效率。

张量操作可以看作是矩阵操作的扩展，适用于更高维度的数据。在深度学习框架如TensorFlow和PyTorch中，张量操作是核心操作之一。

#### 2.1.2 微分与梯度下降法
微分是研究函数变化率的数学分支，它在优化算法中扮演着核心角色。梯度下降法是一种迭代算法，用于求解无约束优化问题。在神经网络中，它被用来最小化损失函数，即找到参数的最优值，以减少预测值和真实值之间的误差。

梯度下降法的基本步骤如下：
1. 初始化参数。
2. 计算损失函数关于参数的梯度。
3. 更新参数：参数 = 参数 - 学习率 * 梯度。
4. 重复步骤2和3，直到收敛。

一个简单的梯度下降法示例代码如下：

def gradient_descent(gradient_func, start, learning_rate, num_iterations):
    params = start
    for _ in range(num_iterations):
        grad = gradient_func(params)
        params = params - learning_rate * grad
    return params

# 示例函数：f(x) = x^2
def f(x):
    return x**2

# 示例函数的梯度：f'(x) = 2x
def f_grad(x):
    return 2*x

# 使用梯度下降法求解函数的最小值
minimum = gradient_descent(f_grad, start=10.0, learning_rate=0.1, num_iterations=10)

### 2.2 概率论与信息论基础

#### 2.2.1 概率分布与期望
在处理不确定性问题时，概率论提供了强有力的工具。在神经网络中，尤其是在生成模型和预测概率输出时，概率分布的概念显得尤为重要。

期望值是概率分布的一个核心概念，它描述了随机变量的平均值。在神经网络中，期望值可以用于计算损失函数的期望梯度，这对于处理包含噪声的数据和进行蒙特卡洛模拟尤其重要。

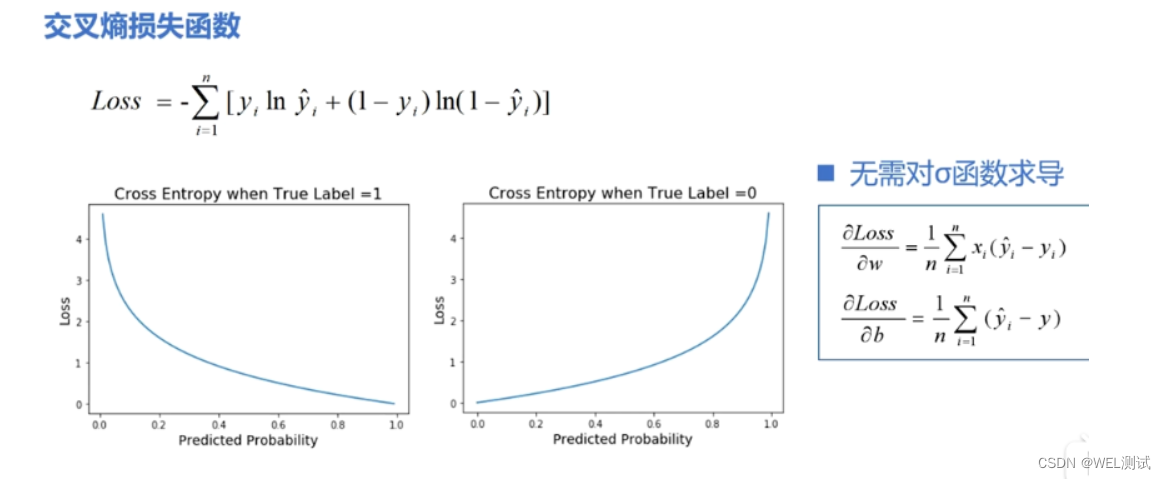
#### 2.2.2 信息熵与交叉熵
信息熵是衡量信息量的一个指标，它描述了一个随机变量的不确定性。在神经网络中，特别是在优化分类问题时，交叉熵作为损失函数在评估模型性能方面起着关键作用。

交叉熵定义为两个概率分布之间的差异度量，它描述了用一个分布来表示另一个分布所需的编码长度。在分类任务中，交叉熵损失函数可以使得模型输出的概率分布与真实标签的概率分布更为接近。

### 2.3 优化理论基础

#### 2.3.1 优化问题的分类
优化问题可以分为无约束优化和有约束优化两大类。神经网络的训练主要集中在无约束优化问题，目标是最小化损失函数。然而，在现实世界的问题中，常常需要考虑额外的约束条件，如参数范数限制或不等式约束。

优化问题的不同类别要求使用不同的算法来求解。例如，拉格朗日乘数法常用于解决带有等式约束的优化问题，而投影梯度下降法可以用于带有不等式约束的优化问题。

#### 2.3.2 常见优化算法介绍
在神经网络训练过程中，常用的优化算法包括随机梯度下降（SGD）、动量SGD、AdaGrad、RMSProp和Adam。每种算法都有其特点和适用场景，选择合适的优化算法对训练速度和模型性能有着显著影响。

例如，动量SGD通过引入动量项来加速学习过程，减少振荡；而Adam算法结合了RMSProp的适应性学习率和动量SGD的优点，能有效避免局部最小值和梯度消失问题。

通过对本小节的阅读，您应该对线性代数在神经网络中的应用、概率论与信息论基础以及优化理论有了更深刻的理解。这些概念不仅是构建和训练神经网络所必需的，也是在面对复杂问题时进行深入分析的基础。

# 3. 神经网络模型结构详解

## 3.1 前馈神经网络

### 3.1.1 网络结构与前向传播

前馈神经网络（Feedforward Neural Network, FNN）是最基本的神经网络类型，其中的信息流是单向的，从输入层到隐藏层再到输出层，没有反向的连接。这种网络结构简单、易于理解，并且是其他复杂网络结构的基础。

在前馈神经网络中，每个神经元只与下一层的神经元相连。网络中的数据从输入层开始，依次通过隐藏层（如果有多个隐藏层的话），最终到达输出层。每层中的神经元不直接相连，也不形成循环。每一层的神经元仅负责接收前一层神经元的输出并产生当前层的输出。

#### 网络结构

- 输入层（Input Layer）：接收外部数据。
- 隐藏层（Hidden Layers）：可以有一个或多个。它们处理输入数据，并将处理后的信息传递给下一层。
- 输出层（Output Layer）：输出网络的最终预测结果。

前向传播（Forward Propagation）是指信息在前馈神经网络中从输入层到隐藏层再到输出层的传播过程。在每一层中，输入数据首先会与该层的权重（weights）进行矩阵乘法，然后加上偏置（bias），再通过激活函数（activation function）转换后，形成该层的输出。这个输出又作为下一层的输入，直到最后一个隐藏层将信息传递到输出层，得到最终的预测值。

import numpy as np

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def forward_pass(X, weights, biases):
    # X: 输入数据
    # weights: 网络中各层的权重
    # biases: 网络中各层的偏置
    # 初始化当前层的输入为输入数据
    current_input = X
    # 遍历每一层进行前向传播
    for weights_layer, biases_layer in zi