选择查找算法与二分查找算法：揭秘其异同与应用场景

# 1. 查找算法概述

查找算法是计算机科学中用于在数据结构中查找特定元素的基本技术。它广泛应用于各种应用中，例如数据库查询、文件搜索和数据分析。查找算法的效率对于系统性能至关重要，因为它们决定了在数据集中查找元素所需的时间和资源。

查找算法有多种类型，每种类型都有其独特的优点和缺点。选择合适的查找算法取决于数据结构、数据集大小和所需的性能要求。常见的查找算法包括线性查找、二分查找、哈希查找和B树查找。

# 2. 选择查找算法

### 2.1 选择查找算法原理

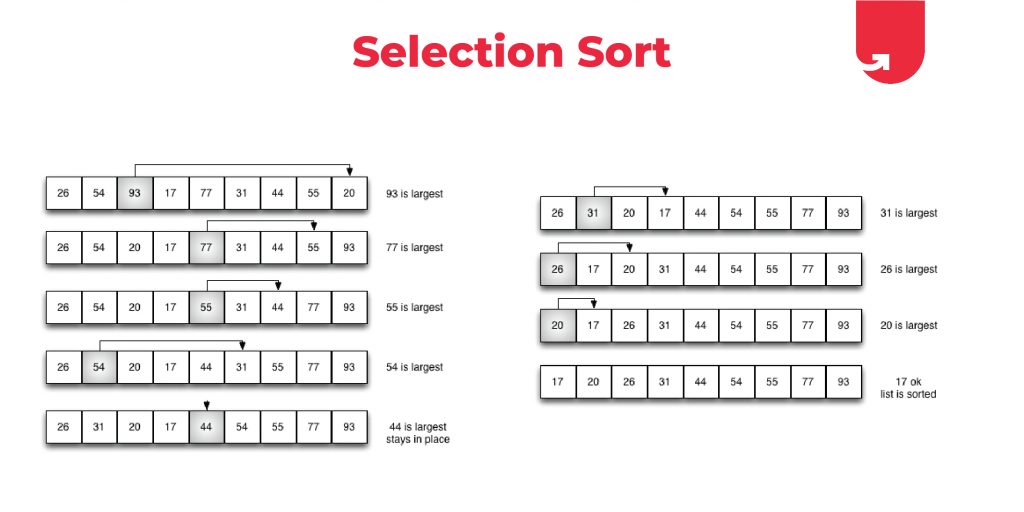
选择查找算法是一种简单且常用的查找算法，其原理如下：

1. **遍历数组：**从数组的第一个元素开始，依次遍历每个元素。
2. **选择最小元素：**在遍历过程中，记录当前遇到的最小元素及其索引。
3. **交换元素：**如果当前元素小于记录的最小元素，则将当前元素与最小元素交换位置。
4. **继续遍历：**重复步骤 1-3，直到遍历完整个数组。
5. **返回结果：**遍历完成后，记录的最小元素的索引即为目标元素在数组中的位置。

### 2.2 选择查找算法时间复杂度

选择查找算法的时间复杂度为 O(n^2)，其中 n 为数组的长度。这是因为该算法需要遍历数组两次：一次查找最小元素，一次交换元素。

### 2.3 选择查找算法的应用场景

选择查找算法适用于以下场景：

- **数组规模较小：**当数组规模较小时，选择查找算法的效率较高。
- **数据无序：**选择查找算法对数据顺序没有要求，因此适用于无序数组。
- **查找次数较少：**如果查找次数较少，选择查找算法的效率也较高。

**代码块：**

def selection_sort(arr):
    """
    选择排序算法

    参数：
        arr: 待排序的数组

    返回：
        排序后的数组
    """

    for i in range(len(arr)):
        min_index = i
        for j in range(i+1, len(arr)):
            if arr[j] < arr[min_index]:
                min_index = j

        arr[i], arr[min_index] = arr[min_index], arr[i]

    return arr

**逻辑分析：**

该代码块实现了选择查找算法。

1. 外层循环遍历数组，记录当前最小元素的索引。
2. 内层循环遍历数组的剩余部分，查找更小的元素。
3. 如果找到更小的元素，更新最小元素的索引。
4. 遍历完成后，将最小元素与当前元素交换位置。

**参数说明：**

- `arr`: 待排序的数组

**返回说明：**

- 排序后的数组

# 3.1 二分查找算法原理

二分查找算法是一种高效的查找算法，适用于已排序的数组或列表。其基本原理是通过不断地将搜索范围对半分，从而快速缩小目标元素的可能位置。

具体来说，二分查找算法的步骤如下：

1. **初始化搜索范围：**将数组的起始索引和结束索引分别设为 0 和数组长度 - 1。
2. **计算中间索引：**计算数组中间索引 `mid`，即 `(start + end) / 2`。
3. **比较目标元素与中间元素：**将目标元素与数组中 `mid` 索引处的元素进行比较。
4. **缩小搜索范围：**根据比较结果缩小搜索范围：
- 如果目标元素等于中间元素，则返回 `mid` 索引。
- 如果目标元素小于中间元素，则将 `end` 索引更新为 `mid - 1`。
- 如果目标元素大于中间元素，则将 `start` 索引更新为 `mid + 1`。
5. **重复步骤 2-4：**重复步骤 2-4，直到搜索范围缩小到一个元素或为空。
6. **返回结果：**如果搜索范围缩小到一个元素且该元素等于目标元素，则返回该元素的索引；否则，返回 -1 表示未找到目标元素。

### 3.2 二分查找算法时间复杂度

二分查找算法的时间复杂度为 O(log n)，其中 n 为数组或列表的长度。这是因为每次迭代都会将搜索范围缩小一半，因此搜索范围的长度以指数级递减。

### 3.3 二分查找算法的应用场景

二分查找算法广泛应用于需要在已排序数据结构中高效查找元素的场景，例如：

- **数组或列表中的元素查找：**二分查找算法可以快速查找数组或列表中是否存在某个元素。
- **数据库查询：**在数据库中，二分查找算法可以用于高效地查找记录。
- **文件系统搜索：**在文件系统中，二分查找算法可以用于快速查找文件或目录。
- **内存管理：**在内存管理中，二分查找算法可以用于快速查找内存块。

# 4. 选择查找算法与二分查找算法的异同

### 4.1 原理上的异同

选择查找算法和二分查找算法在原理上存在本质差异：

- **选择查找算法：**
- 遍历整个数组，逐个比较目标元素与数组元素，找到第一个匹配的元素。
- 适用于无序数组，时间复杂度为 O(n)，其中 n 为数组长度。

- **二分查找算法：**
- 仅适用于有序数组。
- 将数组划分为两个部分，比较目标元素与中间元素，根据比较结果缩小搜索范围。
- 重复上述步骤，直到找到目标元素或确定其不存在。
- 时间复杂度为 O(log n)。

### 4.2 时间复杂度上的异同

选择查找算法和二分查找算法的时间复杂度存在显著差异：

| 算法 | 时间复杂度 |
|---|---|
| 选择查找算法 | O(n) |
| 二分查找算法 | O(log n) |

从表格中可以看出，二分查找算法的时间复杂度远低于选择查找算法，尤其当数组规模较大时，二分查找算法的优势更加明显。

### 4.3 应用场景上的异同

选择查找算法和二分查找算法的应用场景有所不同：

- **选择查找算法：**
- 适用于无序数组或数组规模较小的情况。
- 由于其简单易懂，常用于初学者或非计算机专业人士。

- **二分查找算法：**
- 仅适用于有序数组，且数组规模较大时优势明显。
- 常用于需要快速查找元素的场景，例如数据库查询、文件搜索等。

# 5. 选择查找算法与二分查找算法的应用实践

### 5.1 选择查找算法的应用实例

选择查找算法在实际应用中非常广泛，以下是一些常见的应用场景：

- **数组查找：**选择查找算法可以用于在有序或无序数组中查找特定元素。
- **链表查找：**选择查找算法可以用于在链表中查找特定节点。
- **散列表查找：**选择查找算法可以用于在散列表中查找特定键值对。

# 选择查找算法在数组中的应用
def linear_search(arr, target):
    """
    在数组 arr 中查找目标元素 target

    参数：
        arr: 待查找的数组
        target: 要查找的目标元素

    返回：
        如果找到 target，返回其索引；否则返回 -1
    """
    for i in range(len(arr)):
        if arr[i] == target:
            return i
    return -1

### 5.2 二分查找算法的应用实例

二分查找算法在实际应用中也十分常见，以下是一些常见的应用场景：

- **有序数组查找：**二分查找算法可以用于在有序数组中快速查找特定元素。
- **二叉搜索树查找：**二分查找算法可以用于在二叉搜索树中查找特定节点。
- **数据库查询：**二分查找算法可以用于在数据库中快速查找特定记录。

# 二分查找算法在有序数组中的应用
def binary_search(arr, target):
    """
    在有序数组 arr 中查找目标元素 target

    参数：
        arr: 待查找的有序数组
        target: 要查找的目标元素

    返回：
        如果找到 target，返回其索引；否则返回 -1
    """
    low = 0
    high = len(arr) - 1

    while low <= high:
        mid = (low + high) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1

    return -1