MATLAB特征向量在机器学习中的应用：探索降维与分类（7大算法）

# 1. MATLAB特征向量简介**

特征向量是线性代数中一个重要的概念，它代表了一个线性变换下不改变方向的向量。在MATLAB中，特征向量可以通过特征值分解来计算。

特征值分解是一个将矩阵分解为特征值和特征向量的过程。对于一个n阶方阵A，它的特征值分解可以表示为：

A = V * D * V^-1

其中：

* V是特征向量组成的矩阵，每一列代表一个特征向量。
* D是对角矩阵，对角线上的元素是特征值。
* V^-1是V的逆矩阵。

# 2. 特征向量在机器学习中的应用

特征向量是机器学习中用于数据降维和分类的强大工具。它们可以提取数据的内在结构，并帮助我们以更有效的方式处理复杂数据集。本章将探讨特征向量在机器学习中的各种应用，包括降维和分类。

### 2.1 降维

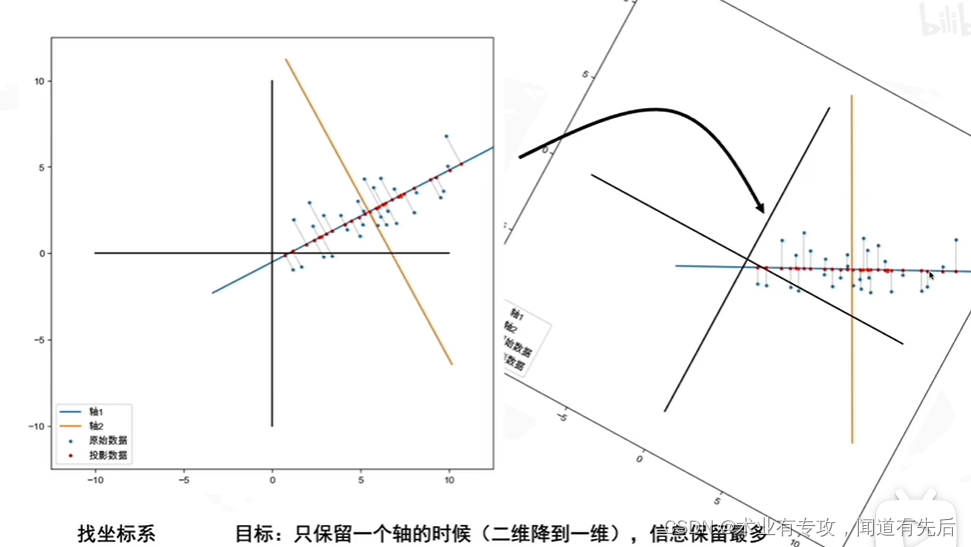
降维是一种将高维数据转换为低维表示的技术。这对于处理大规模数据集非常有用，因为可以显著减少计算复杂度和存储要求。特征向量在降维中发挥着至关重要的作用，因为它可以识别数据的内在结构，并提取最能代表数据方差的特征。

#### 2.1.1 主成分分析（PCA）

PCA是一种流行的降维技术，它通过计算协方差矩阵的特征向量来识别数据中的主成分。主成分是数据方差最大的方向，因此它们可以有效地捕获数据的内在结构。

% 导入数据
data = csvread('data.csv');

% 计算协方差矩阵
cov_matrix = cov(data);

% 计算特征值和特征向量
[eigenvectors, eigenvalues] = eig(cov_matrix);

% 选择主成分
num_components = 2;
principal_components = eigenvectors(:, 1:num_components);

% 降维
reduced_data = data * principal_components;

#### 2.1.2 奇异值分解（SVD）

SVD是另一种降维技术，它通过计算数据矩阵的奇异值和奇异向量来分解数据。奇异值表示数据矩阵的方差，而奇异向量则表示数据矩阵的内在结构。

% 导入数据
data = csvread('data.csv');

% 计算奇异值分解
[U, S, V] = svd(data);

% 选择主成分
num_components = 2;
principal_components = V(:, 1:num_components);

% 降维
reduced_data = U * S * principal_components';

#### 2.1.3 线性判别分析（LDA）

LDA是一种监督降维技术，它通过计算类间散布矩阵和类内散布矩阵的特征向量来识别数据中的判别方向。判别方向是类间方差最大的方向，因此它们可以有效地将不同类别的样本分开。

% 导入数据
data = csvread('data.csv');
labels = csvread('labels.csv');

% 计算类间散布矩阵和类内散布矩阵
Sb = cov(data(labels==1,:)) - cov(data(labels==2,:));
Sw = cov(data(labels==1,:)) + cov(data(labels==2,:));

% 计算特征值和特征向量
[eigenvectors, eigenvalues] = eig(Sb / Sw);

% 选择判别方向
num_components = 2;
discriminant_directions = eigenvectors(:, 1:num_components);

% 降维
reduced_data = data * discriminant_directions;

### 2.2 分类

分类是将数据样本分配到预定义类别的任务。特征向量在分类中发挥着重要作用，因为它可以提取数据的内在结构，并帮助我们构建更有效的分类模型。

#### 2.2.1 支持向量机（SVM）

SVM是一种监督分类算法，它通过在数据空间中找到一个超平面来将不同类别的样本分开。超平面是数据空间中将两类样本分开的最佳决策边界。特征向量可以帮助我们找到数据空间中的线性可分超平