游戏网络中的寻路算法：优化玩家在线体验，减少延迟

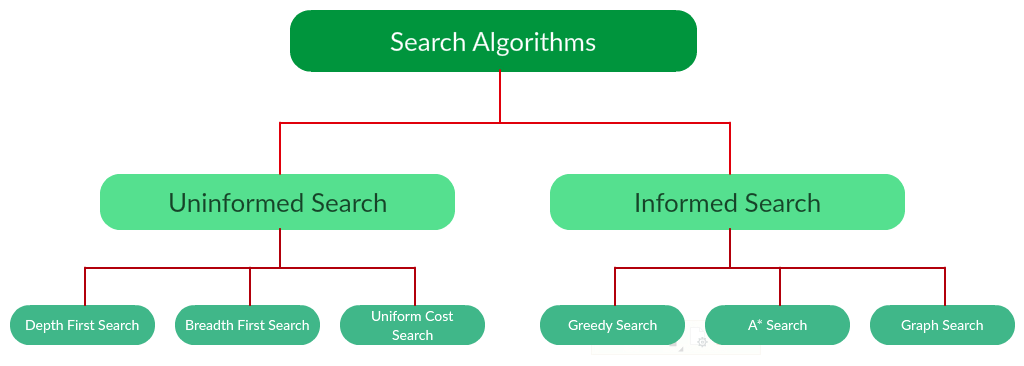
# 1. 寻路算法基础**

寻路算法是计算机科学中用于解决在给定环境中找到从一个点到另一个点的最佳路径的问题的一类算法。在游戏网络中，寻路算法对于角色移动、路径规划和资源收集至关重要。

寻路算法通常基于图论，其中环境被建模为一个由节点（代表位置）和边（代表连接节点的路径）组成的图。寻路算法的目标是找到从源节点到目标节点的具有最小成本或最短距离的路径。

寻路算法的复杂度和效率因算法类型和环境的复杂性而异。在游戏网络中，寻路算法需要快速且高效，以确保平滑的游戏体验。

# 2. 寻路算法在游戏网络中的应用**

## 2.1 路径规划与寻路算法的选型

在游戏网络中，寻路算法是实现角色移动和路径规划的重要技术。路径规划是指根据给定的起点和终点，计算出一条合理的移动路径。寻路算法则负责在游戏世界中找到一条从起点到终点的最优路径。

**路径规划的类型**

路径规划可以分为以下几类：

- **全局路径规划：**从起点到终点规划一条全局最优路径，不受实时环境影响。
- **局部路径规划：**根据实时环境信息，动态规划一条从当前位置到目标位置的局部最优路径。
- **混合路径规划：**结合全局和局部路径规划，先规划一条全局路径，再根据实时环境信息进行局部调整。

**寻路算法的选型**

不同的寻路算法适用于不同的游戏场景和需求。选择寻路算法时需要考虑以下因素：

- **地图规模：**地图越大，寻路算法的计算量越大。
- **障碍物数量：**障碍物越多，寻路算法的复杂度越高。
- **实时性要求：**某些游戏场景要求寻路算法能够实时响应，而另一些场景则可以容忍较长的寻路时间。
- **寻路精度：**某些游戏场景要求寻路算法找到最优路径，而另一些场景则可以容忍次优路径。

## 2.2 寻路算法的性能优化

在游戏网络中，寻路算法的性能优化至关重要。以下是一些常见的优化策略：

- **空间分区：**将游戏世界划分为多个区域，并对每个区域进行独立寻路。
- **寻路缓存：**将经常使用的路径存储在缓存中，以避免重复计算。
- **启发式算法：**使用启发式信息来引导寻路算法，以减少搜索空间。
- **并行寻路：**利用多核处理器或分布式计算来并行执行寻路任务。
- **寻路算法定制：**根据游戏场景的具体需求定制寻路算法，以提高性能。

**代码示例：**

以下代码示例展示了如何使用 A* 寻路算法来规划一条从起点到终点的路径：

import heapq

class Node:
    def __init__(self, x, y, g_cost, h_cost):
        self.x = x
        self.y = y
        self.g_cost = g_cost  # 从起点到当前节点的代价
        self.h_cost = h_cost  # 从当前节点到终点的估计代价
        self.f_cost = self.g_cost + self.h_cost  # 总代价

    def __lt__(self, other):
        return self.f_cost < other.f_cost

class AStar:
    def __init__(self, start, end, map):
        self.start = start
        self.end = end
        self.map = map
        self.open_list = []  # 待探索节点列表
        self.closed_list = set()  # 已探索节点集合
        self.came_from = {}  # 记录每个节点的父节点

    def search(self):
        heapq.heappush(self.open_list, self.start)

        while self.open_list:
            current = heapq.heappop(self.open_list)
            if current == self.end:
                return self.reconstruct_path(current)

            self.closed_list.add(current)

            for neighbor in self.get_neighbors(current):
                if neighbor in self.closed_list:
                    continue

                g_cost = current.g_cost + 1
                h_cost = self.heuristic(neighbor, self.end)
                neighbor.g_cost = g_cost
                neighbor.h_cost = h_cost
                neighbor.f_cost = neighbor.g_cost + neighbor.h_cost

                if neighbor not in self.open_