MATLAB新手速成秘籍：30分钟掌握必备基础知识与实践技巧

# 1. MATLAB简介与环境配置

MATLAB（Matrix Laboratory的缩写），是由MathWorks公司发布的主要面对数值计算、可视化以及编程的高级语言和交互式环境。它广泛应用于工程计算、控制设计、信号处理与通信、图像处理、信号处理、测试和测量、财务建模和分析等领域。

## 1.1 MATLAB的安装与配置

安装MATLAB之前，需要从MathWorks官网下载适合你操作系统的安装包。安装过程中，系统会提示你进行产品密钥的验证和用户账户的注册。安装完成后，配置环境变量，确保系统能够识别MATLAB命令和相关的工具箱。这一部分的操作可能涉及到操作系统级别的配置，详细步骤根据系统不同而有所差异。

## 1.2 MATLAB工作界面简介

首次启动MATLAB时，会出现一个集成的工作界面，包括命令窗口(Command Window)，编辑器(Editor)，工作空间 Workspace，路径和依赖工具 Path and Add-Ons。命令窗口是用户输入命令和查看结果的地方，编辑器用于编写和调试代码，工作空间则显示当前工作区中的变量，路径管理工具能够帮助用户管理各种工具箱和函数库。

## 1.3 MATLAB的版本与更新

MATLAB有多个版本，包括学生版，学术版，工业版等，它们在功能和价格上有所不同。用户可以根据自己的需求选择合适的版本。MathWorks经常会发布软件更新来修复已知问题和添加新功能。你可以通过MATLAB的“Home”界面，点击“Check for Updates”进行在线更新，或者访问MathWorks官网手动下载最新版本。

通过上述内容，我们介绍了MATLAB的基本信息、安装过程以及工作界面的布局，为深入学习MATLAB编程和应用打下了坚实的基础。下一章将着重介绍MATLAB的基础操作和数据类型，带领大家进一步探索MATLAB的世界。

# 2. MATLAB基础操作与数据类型

## 2.1 基本数学运算与矩阵操作

### 2.1.1 算术运算符和矩阵创建

MATLAB是一个高度集成的数值计算环境，其中矩阵是其基本的数学元素。基本的算术运算符包括加（+）、减（-）、乘（*）、除（/）、点乘（.*）、点除（./）和矩阵幂运算（^）。在进行矩阵操作时，这些算术运算符具有不同的含义，比如乘法在不加点的情况下指的是矩阵乘法，加点则表示元素间的逐个乘法。

创建矩阵的方法有很多种，最简单的是直接使用方括号`[]`将元素隔开。例如，创建一个3x3的矩阵A：

A = [1 2 3; 4 5 6; 7 8 9];

上述代码定义了一个3x3的矩阵，其中元素按行排列。也可以使用逗号`,`来分隔行内的元素。创建矩阵的另一种方式是使用函数，例如`zeros`、`ones`、`rand`、`eye`分别用来创建全零矩阵、全一矩阵、随机矩阵和单位矩阵。

### 2.1.2 矩阵的维度和运算规则

矩阵的维度对于确定如何进行矩阵运算至关重要。在MATLAB中，`size`函数可以用来获取矩阵的行数和列数，而`length`函数返回矩阵中最长维度的大小。对于矩阵运算，MATLAB遵循线性代数的规则，例如矩阵乘法要求左矩阵的列数与右矩阵的行数相同。

在进行矩阵乘法时，MATLAB使用`*`运算符，而元素间的逐个乘法则使用`.*`运算符。例如：

B = [1 2 3];
C = [4; 5; 6];
D = B * C; % 这将进行矩阵乘法
E = B .* C; % 这将进行元素逐个乘法

在MATLAB中，矩阵的乘法运算是非常高效的，利用优化过的矩阵库来处理这些计算，为数值分析和工程计算提供了极大的便利。如果矩阵A是一个n×m矩阵，矩阵B是一个m×p矩阵，那么它们的乘积C将是一个n×p矩阵，其中C中的每一个元素是通过矩阵A的一行与矩阵B的一列对应元素相乘后求和得到的。

## 2.2 变量与数据类型

### 2.2.1 变量的声明与赋值

在MATLAB中，变量不需要显式的声明类型，当对变量进行赋值操作时，MATLAB会自动创建相应的变量并指定其数据类型。例如：

x = 10;          % 创建一个整数变量x并赋值为10
y = 3.14;        % 创建一个浮点数变量y并赋值为3.14
z = 'hello';     % 创建一个字符串变量z并赋值为"hello"

这种动态类型特性让MATLAB在快速原型开发中非常有用，但需要注意的是，变量的动态创建可能会影响到程序的性能和内存使用。

### 2.2.2 常见数据类型及转换方法

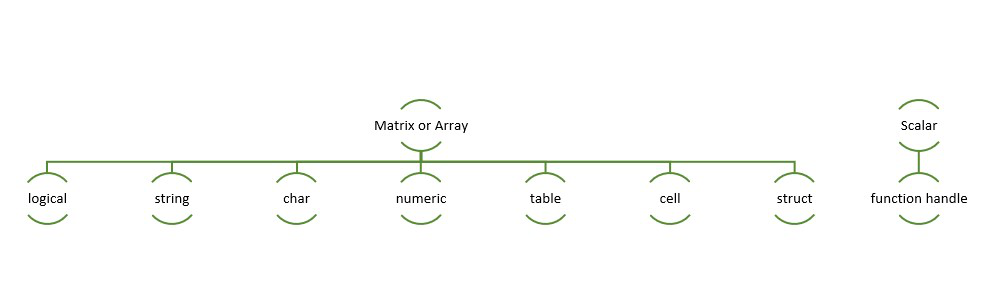
MATLAB支持多种数据类型，包括但不限于整数类型、双精度浮点数、复数、字符和字符串、逻辑类型、单元格数组和结构体等。数据类型的转换可以通过内置函数来实现，例如：

int_var = int32(3.14);     % 将浮点数转换为32位整数
double_var = double('123'); % 将字符串转换为双精度浮点数
char_var = char(65);        % 将数值65转换为对应的ASCII字符

在进行数据类型转换时，必须确保转换后的数据类型能够正确地表达原始数据。例如，将较大的整数转换为较小的整数类型可能会导致溢出，而将浮点数转换为整数则会丢失小数部分。

## 2.3 函数与脚本文件

### 2.3.1 内置函数的使用与创建

MATLAB内置了大量的数学、统计、工程计算和信号处理等领域的函数，例如`sin`、`mean`、`fft`等。调用函数非常简单，只需要指定函数名并传入相应的参数即可。例如计算数组的平均值：

data = [1 2 3 4 5];
mean_value = mean(data);

用户也可以创建自己的函数，函数文件的命名应以`.m`为后缀。创建自定义函数时，可以使用`function`关键字定义函数名和输入输出参数。例如，一个简单的加法函数定义如下：

function result = add(a, b)
    % 这是一个简单的加法函数，返回a和b的和
    result = a + b;
end

### 2.3.2 脚本文件的编写与执行

脚本文件是包含一系列MATLAB语句的文件，与函数不同的是，脚本不接受输入参数也不返回输出参数，它只是执行一系列操作。脚本文件同样以`.m`为后缀，并且可以直接在MATLAB命令窗口中运行。编写一个简单的脚本，将变量a和b的值打印出来：

% script_example.m
a = 5;
b = 10;
disp(['The sum of a and b is ', num2str(a+b)]);

创建了脚本文件之后，可以直接在MATLAB命令窗口中调用该脚本：

>> script_example
The sum of a and b is 15

脚本文件的执行将按照文件内语句的顺序进行，直到文件结束。脚本非常适合用于快速执行一系列操作，但其缺点是没有参数传递机制，对于需要重用和模块化的代码，更适合使用函数。

# 3. MATLAB编程基础

## 3.1 控制流语句

MATLAB中的控制流语句对于编写复杂程序是必不可少的。这些语句允许程序根据条件执行不同的代码块，并能够重复执行某些任务直到满足特定条件。

### 3.1.1 条件语句（if-else结构）

在MATLAB中，条件语句是通过if、elseif和else关键字来实现的。这些结构允许你根据一个或多个条件的真假来控制程序的执行流程。

if condition1
    % Code block if condition1 is true
elseif condition2
    % Code block if condition1 is false and condition2 is true
else
    % Code block if both condition1 and condition2 are false
end

- `condition1` 和 `condition2` 是布尔表达式，它们的值可以是 `true` 或 `false`。
- 代码块是被 `if`、`elseif` 或 `else` 关键字包围的指令序列。

**逻辑分析**：上述结构首先评估 `condition1`。如果为真，则执行第一个代码块。如果为假，它将检查 `condition2`。只有当 `condition1` 和 `condition2` 都为假时，才会执行 `else` 部分的代码块。`end` 关键字标志着条件语句的结束。

### 3.1.2 循环语句（for, while）

循环语句用于重复执行一段代码，直到满足特定条件。

#### for循环

`for` 循环用于迭代固定次数的循环。

for index = start:increment:end
    % Code block to execute repeatedly
end

- `index` 是循环变量。
- `start` 是循环开始值。
- `increment` 是每次迭代循环变量增加的值。
- `end` 是循环结束值。

**逻辑分析**：`for` 循环的执行次数在循环开始之前就已经确定。循环变量从 `start` 值开始，每次迭代增加 `increment` 值，直到达到或超过 `end` 值为止。

#### while循环

`while` 循环用于条件满足时执行代码块，循环次数不确定。

while condition
    % Code block to execute repeatedly
end

- `condition` 是一个布尔表达式。

**逻辑分析**：只要 `condition` 的值为 `true`，`while` 循环内的代码块就会不断执行。需要注意的是，循环体内必须包含能够使条件最终变为 `false` 的代码，否则会导致无限循环。

**示例**：

% for 循环示例
for i = 1:5
    disp(['This is iteration number ', num2str(i)]);
end

% while 循环示例
count = 1;
while count < 5
    disp(['Iteration number ', num2str(count)]);
    count = count + 1;
end

## 3.2 函数的高级用法

### 3.2.1 函数句柄的创建与应用

MATLAB 函数句柄是代表函数的变量。它们允许你将函数作为参数传递给其他函数，或存储在数据结构中。

% 创建函数句柄
f = @sin;

- `@` 符号用于创建函数句柄。
- `f` 现在是一个指向 MATLAB 内置 `sin` 函数的句柄。

**逻辑分析**：函数句柄可以像普通函数一样被调用。当你使用函数句柄调用函数时，你可以在任何需要函数名的地方传递这个句柄。

### 3.2.2 变参函数和局部变量

在MATLAB中，可以编写变参函数来接受不同数量的输入参数。局部变量只在函数内部可见，它们不会影响到函数外部的变量。

function result = myVarArgsFunction(varargin)
    % varargin is a cell array containing all the input arguments
    sum = 0;
    for i = 1:length(varargin)
        sum = sum + varargin{i};
    end
    result = sum;
end

- `varargin` 是一个特殊的变量，代表一个可变数量的输入参数。
- `varargin` 在函数内部被处理为一个cell数组。
- 变参函数使得函数调用更加灵活。

**逻辑分析**：上述函数 `myVarArgsFunction` 可以接受任意数量的输入参数，并计算它们的总和。函数的参数是通过 `varargin` cell数组来访问的，这样就可以在不预先知道参数数量的情况下，编写能够处理任意参数的函数。

## 3.3 调试和优化代码

### 3.3.1 调试技巧与工具

MATLAB提供了一系列工具用于调试代码。使用这些工具可以帮助你发现程序中潜在的问题并纠正错误。

- **错误消息**: MATLAB在遇到语法错误或者运行时错误时会显示错误消息。
- **M-Lint**: 这是一个代码分析工具，可以提供代码风格和结构上的建议。
- **断点**: 可以在代码编辑器中设置断点，然后逐步执行代码，检查变量值和程序状态。
- **数组查看器**: 当调试时，可以使用数组查看器查看和修改变量的值。

### 3.3.2 代码性能分析与优化

代码的性能分析是指找出程序中运行缓慢的部分，并对其进行优化的过程。MATLAB提供了性能分析工具（如 `profile`），可以用来分析代码的运行时间和内存使用。

profile on
% 执行你的代码
profile off
report = profile report;
disp(report);

- `profile on` 开始性能分析。
- 执行需要分析的代码部分。
- `profile off` 停止性能分析。
- `profile report` 生成性能分析报告。

**逻辑分析**：运行上述代码后，MATLAB会收集关于代码执行时间和内存使用的统计信息，并生成一个详细的报告。报告中会包含函数调用次数，每个函数花费的时间以及内存消耗等信息。这些数据有助于开发者识别程序中的性能瓶颈并采取相应的优化措施。

**示例**：

% 性能分析示例
profile on
for i = 1:1000
    A = rand(1000);
    B = A * A;
end
profile off

report = profile report;
disp(report);

上述示例中，我们首先开启性能分析，然后执行一个会消耗一定时间的矩阵乘法操作，最后停止性能分析并显示报告。这样我们就可以根据报告内容评估和优化矩阵乘法操作的代码段了。

# 4. MATLAB数据可视化

### 4.1 基本图形的绘制

在进行科学计算和数据分析的过程中，数据可视化是至关重要的一步。它可以帮助我们更好地理解数据，揭示隐藏在数据背后的模式和趋势。MATLAB提供了强大的图形绘制功能，支持从基本的二维图形到复杂的三维图形以及动态更新的图形。

#### 4.1.1 二维图形的绘制方法

MATLAB中的二维图形包括折线图、条形图、散点图、饼图、直方图等，它们可以用于展示数据的统计特性。例如，折线图适合展示随时间变化的趋势，而散点图则适合展示两个变量间的相关性。

下面是一段使用MATLAB绘制一个简单二维折线图的示例代码：

x = 0:0.01:1; % 定义x的取值范围，从0到1，步长为0.01
y = sin(2*pi*x); % 定义y的表达式，这里以正弦函数为例
plot(x, y); % 绘制折线图
title('Simple 2D Line Plot'); % 设置图表标题
xlabel('x values'); % 设置x轴标签
ylabel('sin(2*pi*x)'); % 设置y轴标签
grid on; % 打开网格

在上述代码中，`plot` 函数是MATLAB中最基础的绘图函数，用于绘制二维图形。该函数的参数 `x` 和 `y` 分别表示数据点的横纵坐标。`title`、`xlabel` 和 `ylabel` 函数分别用于设置图表的标题和坐标轴标签。最后，`grid on` 用于打开图表的网格线，以便更清晰地查看数据点。

#### 4.1.2 三维图形的绘制技巧

当需要展示三维数据关系时，MATLAB的三维图形绘制功能就显得尤为重要。常见的三维图形包括三维线图、散点图、曲面图等。三维图形可以提供更多的视角来观察数据，尤其在数据结构较为复杂时，可以更直观地表达数据之间的关系。

下面是一个绘制三维散点图的示例代码：

[x, y] = meshgrid(-5:0.5:5, -5:0.5:5); % 生成网格数据
z = sin(sqrt(x.^2 + y.^2)); % 定义z的取值，这里利用了x和y的网格数据来计算z
scatter3(x, y, z); % 绘制三维散点图
title('Simple 3D Scatter Plot'); % 设置图表标题
xlabel('x values'); % 设置x轴标签
ylabel('y values'); % 设置y轴标签
zlabel('sin(sqrt(x^2 + y^2))'); % 设置z轴标签
grid on; % 打开网格

在上面的代码中，`meshgrid` 函数用于生成网格数据点，`scatter3` 函数则是用于绘制三维散点图。三维图形的视角可以通过鼠标进行拖拽和旋转，以便从不同角度观察数据。

### 4.2 图形的修饰与导出

绘制好的图形通常需要进行适当的修饰来提高可读性和美观性。MATLAB允许用户调整图形的颜色、线条样式、标记样式、图例、坐标轴的范围和标签等。

#### 4.2.1 图形属性的设置

MATLAB提供了丰富的图形属性设置选项，包括线条颜色、线条宽度、标记样式等。这些设置可以帮助我们突出显示特定的数据点或者趋势，同时也可以让图形更加吸引人的眼球。

下面的代码片段演示了如何设置线条颜色、添加图例，并指定标记样式：

% 绘制一个带有自定义属性的二维图形
x = linspace(0, 2*pi, 100);
y1 = sin(x);
y2 = cos(x);
plot(x, y1, 'r--', x, y2, 'b.-'); % 绘制红色虚线和蓝色点线
legend('sin(x)', 'cos(x)'); % 添加图例
title('Customized Line Plot'); % 设置标题
xlabel('x values'); % 设置x轴标签
ylabel('Function values'); % 设置y轴标签
grid on; % 打开网格

#### 4.2.2 图形的保存与导出格式

完成图形绘制和修饰后，我们可以将图形保存为常见的图像格式，例如PNG、JPEG、BMP等。此外，MATLAB还支持将图形保存为矢量图形格式如EPS和PDF，这对于保持图形的高质量打印非常有用。

保存图形到文件的命令非常简单：

saveas(gcf, 'myplot.png'); % 保存当前图形窗口为PNG文件

其中，`gcf` 表示当前图形窗口的句柄，`saveas` 函数用于将该窗口保存为指定的文件格式和路径。

### 4.3 动态图形和交互界面

动态图形是指那些能够实时响应数据变化的图形，它们在模拟、动画显示等领域有广泛的应用。MATLAB提供了创建动态图形的工具，如动画制作和交互式GUI设计。

#### 4.3.1 动态更新的图形实现

在MATLAB中，可以利用`update`函数来实现图形的动态更新。通过定时或条件触发，可以改变图形数据源，从而实现动态效果。

下面的示例代码演示了如何实现一个简单的动态更新的折线图：

x = 0:0.01:1; % 初始化x数据
y = zeros(size(x)); % 初始化y数据
f = figure('Position', [100, 100, 400, 300]); % 创建图形窗口
ax = gca; % 获取当前坐标轴
ax.YLim = [-1, 1]; % 设置y轴范围
h = plot(ax, x, y, 'r', 'LineWidth', 2); % 绘制红色线条
xlabel('x values');
ylabel('sin(2*pi*x)');
title('Dynamic Line Plot');
for t = 0:0.1:10
    y = sin(2*pi*(x+t)); % 更新y数据
    set(h, 'YData', y); % 更新线条的数据源
    drawnow; % 立即更新图形
end

#### 4.3.2 交互式图形用户界面（GUI）设计

交互式图形用户界面（GUI）的设计是MATLAB应用的一个重要方面，它允许用户与图形元素进行交互，实现自定义的用户体验。

MATLAB提供的GUI设计工具包括GUIDE和App Designer，这里以App Designer为例介绍一个简单的GUI设计流程：

1. 打开App Designer。
2. 通过拖放控件来设计应用界面。
3. 在“代码视图”中编写回调函数，定义控件行为。
4. 运行并测试App。
5. 使用`saveApp`函数保存设计好的App。

下面是一个使用App Designer创建的简单GUI应用的代码片段，该应用包含一个滑动条和一个图形显示区域：

classdef SimpleGUIApp < matlab.apps.AppBase

    % Properties that correspond to app components
    properties (Access = public)
        UIFigure              matlab.ui.Figure
        Axes                  matlab.ui.control.UIAxes
        Slider                matlab.ui.control.UIRangeSlider
        StartButton           matlab.ui.control.UIButton
    end
    properties (Access = private)
        PlotHandle            matlab.graphics.axis.Axes
    end

    methods (Access = private)

        % Callback function for Slider change
        function SliderValueChanged(app, event)
            value = app.Slider.Value;
            % 假设这里是绘图的代码，根据滑动条的位置更新图形
        end
        % Callback function for Start button click
        function StartButtonPushed(app, event)
            % 初始化图形数据
            % 绘制图形到app.Axes
        end
    end

    % App initialization and construction
    methods (Access = private)
        % 创建UI组件并设置布局
        function createComponents(app)
            % 创建Figure窗口
            app.UIFigure = uifigure('Name', 'Simple GUI');
            % 其他UI组件创建...
        end
    end

    % App启动时触发的函数
    methods (Access = public)

        % Construct app
        function app = SimpleGUIApp
            % 创建并配置组件
            createComponents(app)
            % 其他初始化代码...
        end
    end
end

在上述代码中，我们创建了一个名为`SimpleGUIApp`的类，其中包含了创建和操作GUI的代码。`createComponents`方法用于初始化组件，`SliderValueChanged`和`StartButtonPushed`方法则分别对应滑动条和按钮的回调函数，用于响应用户操作。

通过上述章节的介绍，我们已经了解了MATLAB如何实现数据可视化，包括基本图形的绘制、图形的修饰与导出以及动态图形和交互界面的设计。这些技巧对于展示和分析数据至关重要，能够帮助我们更加直观和有效地传达信息。随着对MATLAB数据可视化功能的深入理解和实践，您将能够创建更加复杂和美观的图形，进而提高您在科学计算和工程应用中的表现。

# 5. MATLAB实践应用示例

## 5.1 工程问题求解

### 5.1.1 数值计算方法应用

数值计算在工程问题求解中扮演着核心角色。MATLAB提供了一系列强大的数值计算功能，可以从简单的线性方程求解到复杂的偏微分方程求解。在本小节中，我们将探索如何使用MATLAB进行数值积分和微分方程求解。

首先来看数值积分，MATLAB内置了多种数值积分函数，例如`integral`函数，可以用来计算定积分。例如，要求解函数`f(x) = x^2`从0到1的定积分，我们可以编写如下代码：

f = @(x) x.^2; % 定义函数
integral_value = integral(f, 0, 1);

此代码段定义了一个匿名函数`f`，并计算了其在区间[0,1]上的定积分值。

对于微分方程求解，MATLAB的`ode45`、`ode23`等函数非常实用。这些函数基于经典的Runge-Kutta方法，可以求解一阶常微分方程初值问题。考虑一个简单的一阶微分方程`dy/dx = y`，给定初始条件`y(0) = 1`，我们可以使用以下代码来求解：

% 定义微分方程 dy/dx = f(x,y)
f = @(x, y) y;
% 初始条件
y0 = 1;
% 求解区间
xspan = [0 10];
% 使用ode45求解器求解
[x, y] = ode45(f, xspan, y0);

代码中定义了一个函数句柄`f`，并利用`ode45`求解器来求解微分方程。MATLAB会返回在指定区间`xspan`内的解向量`x`和`y`。

### 5.1.2 优化问题的MATLAB解决方案

优化问题广泛应用于工程和科学领域，例如资源分配、设计优化、参数估计等。MATLAB的优化工具箱提供了包括线性规划、非线性规划、整数规划等多种优化方法。以下我们通过一个实例来演示如何使用MATLAB解决一个简单的非线性优化问题。

假设我们有如下非线性目标函数和约束条件：

min f(x) = x1^2 + x2^2
s.t.
x1 + x2 = 10
x1 >= 0
x2 >= 0

MATLAB代码实现如下：

% 定义目标函数
f = @(x) x(1)^2 + x(2)^2;

% 约束条件
Aeq = [1 1];
beq = 10;
lb = [0 0]; % 变量下界

% 优化选项设置
options = optimoptions('fmincon','Display','iter','Algorithm','interior-point');

% 求解优化问题
[x, fval] = fmincon(f,[1,1],[],[],Aeq,beq,lb);

disp(['最小值为: ', num2str(fval)]);
disp(['对应的x值为: ', num2str(x)]);

在此代码中，我们首先定义了目标函数`f`，然后指定了等式约束和变量的下界。通过`fmincon`函数求解非线性约束优化问题，其中`[1,1]`是初始猜测解。优化求解器会迭代计算，直到找到满足约束条件的最小值。

通过本小节的介绍，我们了解了MATLAB在工程问题求解中的应用，包括数值计算方法和优化问题解决方法。这仅仅是一个起点，MATLAB提供了更深层次的工具和方法以供深入研究和应用。

## 5.2 信号处理与分析

### 5.2.1 傅里叶变换与频谱分析

傅里叶变换是信号处理中的一个基石，它允许我们分析信号的频率成分。MATLAB提供了一个强大的工具——`fft`函数，用于计算离散傅里叶变换（DFT）。在本小节中，我们将了解如何利用MATLAB实现傅里叶变换，并进行频谱分析。

我们首先创建一个简单的信号，例如一个包含多种频率成分的复合信号，然后使用`fft`函数进行变换。以下是MATLAB代码：

% 定义时间向量
t = 0:0.001:1;
% 信号由两个正弦波组成
f1 = 50; % 频率50Hz
f2 = 120; % 频率120Hz
signal = sin(2*pi*f1*t) + 0.5*sin(2*pi*f2*t);

% 计算信号的FFT
N = length(signal); % 信号长度
Y = fft(signal);
P2 = abs(Y/N);
P1 = P2(1:N/2+1);
P1(2:end-1) = 2*P1(2:end-1);

% 定义频率域f
f = (f1:N/2)*fs/N;

% 绘制信号的频谱
figure;
plot(f,P1);
title('Single-Sided Amplitude Spectrum of S(t)');
xlabel('f (Hz)');
ylabel('|P1(f)|');

代码中我们首先定义了信号`signal`，然后计算了其快速傅里叶变换`Y`。变换结果`Y`是一个复数向量，其中包含了信号的幅度和相位信息。通过取`Y`的绝对值并进行适当的缩放和处理，我们得到了信号的单侧幅度频谱。

### 5.2.2 滤波器设计与应用

滤波器是信号处理中另一个重要的组成部分，用于控制信号中频率成分的通过与抑制。MATLAB的信号处理工具箱提供了设计和实现数字滤波器的方法，包括FIR和IIR滤波器。以下我们将使用MATLAB设计一个低通滤波器，并将其应用到信号上。

首先，我们需要确定滤波器的设计规格，例如截止频率、通带和阻带纹波等。设计滤波器的代码如下：

% 滤波器设计规格
Fs = 1000; % 采样频率
Fc = 150; % 截止频率
N = 6; % 滤波器阶数
Wn = Fc/(Fs/2); % 归一化截止频率

% 使用fdatool或者函数设计滤波器
[b, a] = butter(N, Wn);

% 使用滤波器
filtered_signal = filter(b, a, signal);

% 绘制滤波器前后信号
figure;
subplot(2,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, filtered_signal);
title('Filtered Signal');
xlabel('Time (s)');
ylabel('Amplitude');

在这段代码中，我们首先定义了采样频率`Fs`和截止频率`Fc`，然后使用`butter`函数设计了一个N阶巴特沃斯低通滤波器。`filter`函数用于将滤波器应用到原始信号上。最后，我们绘制了原始信号和滤波后信号的图形，以直观展示滤波效果。

通过本小节的介绍，我们学习了傅里叶变换在频谱分析中的应用，以及如何设计和使用数字滤波器来处理信号。MATLAB在信号处理方面提供了强大的工具，使得复杂的信号处理任务变得简单和直观。

## 5.3 数据处理与统计分析

### 5.3.1 数据的导入导出与预处理

在进行数据分析之前，我们首先需要处理数据，包括导入、导出、清洗和转换等预处理步骤。MATLAB为数据的预处理提供了强大的支持。在本小节中，我们将探讨如何使用MATLAB进行数据的导入导出与预处理。

首先，导入外部数据到MATLAB中，常用函数有`load`、`csvread`、`xlsread`等。例如，从CSV文件中读取数据，我们可以使用如下命令：

% 假设有一个名为data.csv的CSV文件
data = csvread('data.csv');

数据导入后，通常需要进行预处理，比如数据清洗、格式转换、缺失值处理等。例如，假设我们从某传感器获取的数据中有一些缺失值，可以用如下方式处理：

% 假设data矩阵中第一列有缺失值
% 将缺失值用所在列的平均值替代
data(:,1) = fillmissing(data(:,1), 'mean');

对于数据的导出，MATLAB也提供了多个函数，例如`save`、`csvwrite`、`xlswrite`等。例如，将数据导出到CSV文件，我们可以使用如下命令：

% 假设要将data矩阵导出到data_out.csv文件
csvwrite('data_out.csv', data);

在进行统计分析前，对数据进行预处理是非常关键的一步，因为数据质量直接影响分析结果的准确性。

### 5.3.2 描述统计与假设检验

在数据预处理之后，下一步通常是进行描述统计和假设检验。描述统计包括均值、方差、标准差等基本统计量的计算，而假设检验用于验证数据的某些统计假设是否成立。

MATLAB提供了很多方便的函数来完成这些任务。例如，使用`mean`、`var`、`std`函数可以计算均值、方差和标准差：

% 假设data矩阵中的第一列是我们感兴趣的变量
mean_value = mean(data(:,1));
variance_value = var(data(:,1));
std_value = std(data(:,1));

在进行假设检验时，MATLAB的统计工具箱提供了`ttest`、`ANOVA`等多种检验方法。例如，进行一个t检验来判断两个样本均值是否有显著差异：

% 假设有两个独立样本x和y
x = [1,2,3,4,5];
y = [3,4,5,6,7];

% 进行双尾t检验
[h, p, ci, stats] = ttest2(x, y);

在这里，`ttest2`函数执行了一个独立样本的双尾t检验。`h`是检验结果的逻辑值，`p`是p值，`ci`是置信区间，`stats`包含了检验的统计量。

通过本小节的介绍，我们看到了MATLAB在数据处理和统计分析方面强大的功能，无论是从数据导入导出，还是进行描述统计和假设检验，MATLAB都提供了方便快捷的方法。这些工具使得数据分析工作更加高效和准确。

# 6. MATLAB编程进阶与扩展

随着对MATLAB基础操作和编程的掌握，用户常常需要解决更复杂的工程问题或与其他编程语言进行交互。在本章中，我们将进一步探讨MATLAB的面向对象编程基础，以及与其他语言如C/C++和Python的交互方式。此外，我们还将介绍如何安装和配置各种工具箱，以及如何有效地利用MATLAB用户社区资源。

## 6.1 面向对象编程基础

MATLAB的面向对象编程能力允许用户创建和管理复杂的项目和代码库。理解和应用面向对象编程能够提升代码的可读性、可维护性以及复用性。

### 6.1.1 类与对象的概念

在MATLAB中，类是创建对象的蓝图或模板。对象则是根据这个蓝图生成的具体实例。一个类包括数据（属性）和可以操作这些数据的方法。

% 定义一个简单的类
classdef Person
    properties
        Name
        Age
    end
    methods
        function obj = Person(name, age)
            obj.Name = name;
            obj.Age = age;
        end
        function displayAge(obj)
            fprintf('Name: %s, Age: %d\n', obj.Name, obj.Age);
        end
    end
end

### 6.1.2 类的属性和方法

属性是类的变量部分，代表对象的状态。方法是类的函数部分，代表对象的行为。在MATLAB中，可以通过点号（`.`）操作符访问对象的属性和方法。

% 创建一个Person类的实例
john = Person('John Doe', 30);

% 调用方法显示年龄
john.displayAge();

## 6.2 MATLAB与其他语言的交互

MATLAB提供了与其他编程语言交互的途径，这使得开发者可以利用不同语言的优势，为特定任务选择合适的工具。

### 6.2.1 MATLAB与C/C++的接口调用

通过MATLAB提供的一些API和编译器工具，开发者可以将C或C++编写的代码集成到MATLAB环境中。这通常是通过MATLAB的MEX接口实现的，允许直接在MATLAB中调用C/C++函数。

% 假设已经编写了名为mymexfunction.c的C语言文件
mex mymexfunction.c
result = mymexfunctionargin1,argin2);

### 6.2.2 MATLAB与Python的交互操作

MATLAB与Python之间的交互变得越来越受欢迎，因为Python在数据分析和机器学习领域非常流行。MATLAB与Python的交互可以通过MATLAB的Python接口进行。

% 在MATLAB中启动Python解释器
py.PythonAPI.Initialize;
% 调用Python函数
pyresult = py exec("import sys; print(sys.version)");
disp(pyresult)

## 6.3 开发工具箱和用户社区

MATLAB提供了丰富的工具箱以支持不同领域的专业应用。同时，MATLAB用户社区是获取帮助和分享资源的重要平台。

### 6.3.1 工具箱的安装与配置

开发者可以根据需要安装各种工具箱，这些工具箱提供了专业领域的高级函数和应用示例。工具箱通常通过MATLAB的Add-On Explorer进行安装。

% 搜索特定的工具箱
searchResults = matlab.addons.search('Image Processing Toolbox');
% 安装工具箱
matlab.addons.install(searchResults(1).ID);

### 6.3.2 用户社区资源的利用与分享

用户社区提供了问题解答、代码示例、技术文章等资源。用户可以在这里找到问题的解决方案，也可以分享自己的经验和代码。

% 打开MATLAB用户社区
web('https://www.mathworks.com/matlabcentral');

通过本章的内容，您可以了解到MATLAB的面向对象编程基础，以及如何与其它编程语言进行交互，同时也学习到如何更好地利用MATLAB强大的工具箱和社区资源。这些知识的掌握，将为您的MATLAB学习旅程带来质的飞跃。在后续章节中，我们将进一步深入这些话题，并结合实际案例，展示如何在专业领域应用这些高级技术。