加权平均法在模糊控制中的稳定性分析:理论与实践
发布时间: 2025-01-04 20:05:38 阅读量: 7 订阅数: 12 


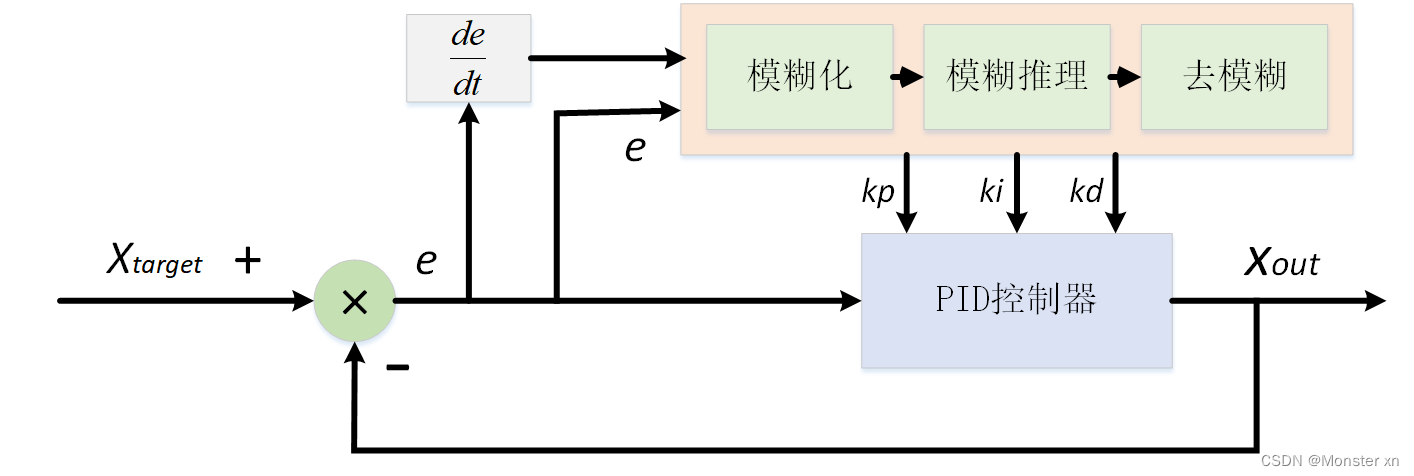
工业电子中的模糊pid控制器在复杂控制中的应用
# 摘要
加权平均法作为控制理论中的重要概念,适用于模糊逻辑控制中以提高系统的精确度与稳定性。本文首先介绍加权平均法及其在控制理论中的作用,随后深入探讨模糊逻辑与控制理论基础,并分析了加权平均法的数学原理及其在模糊控制中的应用。文章进一步展示了稳定性分析的理论模型与方法,并通过实验设计与案例研究,探讨了加权平均法在模糊控制稳定性分析中的实践。最后,展望了技术进步对于改进加权平均法在模糊控制稳定性分析中的影响,以及模糊控制系统所面临的挑战和未来发展方向。
# 关键字
加权平均法;模糊逻辑;控制理论;稳定性分析;模糊控制;人工智能
参考资源链接:[模糊控制理论详解:加权平均法在模糊系统中的应用](https://wenku.csdn.net/doc/89pmt2n5co?spm=1055.2635.3001.10343)
# 1. 加权平均法简介及其在控制理论中的作用
在现代控制理论中,加权平均法作为一种有效的系统分析工具,广泛应用于不同控制系统的设计和优化过程中。这种方法的核心在于通过为各个控制输入分配权重,以达到更为精确和稳定的效果。本章将首先对加权平均法进行基本概念的介绍,并探讨其在控制理论中的基础性作用。
## 1.1 加权平均法基本概念
加权平均法是一种数学统计方法,其主要目的是通过分配不同的权重来平均数值数据。与传统平均法不同,加权平均法根据数据的重要性或可靠性为不同的数据点赋予不同的权重。这种方法不仅能够有效反映数据集的总体情况,而且能够更加贴合实际,提高评估和决策的准确性。
## 1.2 加权平均法在控制理论中的作用
在控制理论中,加权平均法被用来评估和优化控制系统的关键参数,如比例、积分和微分(PID)控制器的输出。通过合理地调整权重,控制系统能够在面对不确定性和扰动时保持稳定,从而提高整个系统的性能和可靠性。这种调整不仅可以是静态的,也可以是动态的,以适应不断变化的环境条件。
## 1.3 加权平均法与控制理论的结合
将加权平均法应用到控制理论中,可以实现对系统输出的精确调控。例如,在设计模糊控制器时,可以将不同控制规则的可信度作为权重,进而计算出更加合理的控制命令。这种结合不仅强化了控制系统的灵活性和适应性,而且也提高了处理复杂问题的能力。随着更多先进的计算方法和理论的发展,加权平均法在控制理论中的应用将会更加广泛和深入。
通过本章的学习,读者将对加权平均法有一个初步的认识,并了解其在控制理论中的重要性与应用价值。在后续章节中,我们将深入探讨加权平均法的理论框架,及其在模糊控制和稳定性分析中的实际应用。
# 2. 模糊逻辑与控制理论基础
## 2.1 模糊逻辑的基本概念
### 2.1.1 模糊集合理论
模糊集合理论是模糊逻辑的基础,其核心思想在于放松传统集合论中的二值逻辑(即一个元素要么属于一个集合,要么不属于一个集合,没有中间状态)限制,允许集合中的元素具有部分隶属度。换句话说,一个元素可以以0到1之间的任何数值属于一个模糊集合。这种部分隶属的概念能够更好地描述现实世界中的不确定性和模糊性。
为了更深入地理解模糊集合,我们可以借助于一个简单的例子。考虑一个描述“高个子”的模糊集合,一个具体的人,比如说身高为180厘米,可以有一个隶属度,比如0.7,这意味着他相对较高,但不是绝对的高个子,这个隶属度取决于我们对于“高个子”这个词的定义。隶属函数可以是线性的,也可以是非线性的,这取决于我们如何定义该集合。
在模糊逻辑中,隶属函数的定义至关重要,因为它直接影响到模糊推理的准确性和系统的表现。定义一个好的隶属函数需要深入了解领域知识以及实际应用中的需求。
### 2.1.2 模糊规则和模糊推理
模糊规则是模糊控制系统中的核心组件之一,它根据模糊逻辑表达式建立输入(前件)和输出(后件)之间的映射关系。例如,一个简单的模糊规则可能是:“如果温度很高且湿度很大,则冷却系统应该快速工作。” 在这个规则中,“温度很高”和“湿度很大”是模糊规则的前件,而“冷却系统应该快速工作”是后件。
模糊推理是根据模糊规则和输入的实际测量值来推导系统输出的过程。这种推理不是基于精确逻辑而是基于模糊逻辑,意味着它不是返回一个明确的输出,而是输出一个属于某个模糊集合的隶属度。例如,如果当前温度是30度,湿度是80%,那么根据模糊规则,冷却系统的输出将有一个隶属度,说明系统需要工作的速度。
模糊推理机制主要分为以下几种:
- **Mamdani方法**:最常见的一种模糊推理方法,它使用min-max推理规则来计算输出隶属度。该方法易于理解,直观,特别适用于专家系统和模拟人类决策过程的领域。
- **Sugeno方法**:与Mamdani方法相比,Sugeno方法在输出端使用线性或常数函数,这使得该方法在数学上处理起来更加方便,尤其适合于系统建模和控制。
- **Tsukamoto方法**:这种方法以有序的模糊集合为基础,为每个规则的输出定义一个连续的隶属函数。输出是根据这些隶属函数的加权平均值计算得出,常用于需要保持输出连续性的控制系统。
模糊规则和模糊推理机制是模糊控制器的关键组成部分,它们共同工作以实现对复杂、非线性系统的有效控制。
## 2.2 控制理论概述
### 2.2.1 控制系统的分类
控制系统可以根据其特性和应用领域进行分类。基本的分类方法包括:
- **开环控制系统**:在这类系统中,控制器的输出不依赖于系统的反馈信号。因此,它们对参数变化的适应能力较差,但是结构简单,易于实现。
- **闭环控制系统**:闭环系统(也称为反馈控制系统)将系统的输出反馈到输入端,用于调整控制器的输出。这种系统具有更好的稳定性和抗干扰能力。
- **自适应控制系统**:自适应系统能够根据系统的动态性能自我调整控制器参数。它们通常用于变化的环境或对象参数未知的情况。
- **鲁棒控制系统**:设计用于在面对模型不确定性和外部干扰时保持稳定性的系统。这类系统的重点在于抵抗不确定因素带来的影响。
不同的控制系统有不同的特点,适用于不同的场合。选择合适的系统架构对于实现有效的控制至关重要。
### 2.2.2 控制理论中的稳定性分析
在控制系统中,稳定性分析是确保系统能够在各种条件下可靠运行的基础。稳定性的概念在控制理论中有着严格的数学定义,但是对于控制系统设计者来说,更重要的是了解如何通过稳定性分析来预测和改进系统行为。
稳定性分析主要有以下几种方法:
- **Lyapunov方法**:这是一种能量方法,通过构造一个Lyapunov函数来分析系统是否稳定。如果能够证明随着系统的演进,Lyapunov函数的值不断减小,则系统是稳定的。
- **Routh-Hurwitz准则**:这是一种频率域的方法,通过分析特征方程的根来判断系统的稳定性。如果所有根都位于复平面的左半部分,则系统稳定。
- **Bode图和Nyquist图**:这些图是频率响应分析的一部分,用于观察系统增益和相位随频率变化的情况,进而判断系统稳定性。
稳定性分析是控制系统设计和实施的关键环节,它直接关系到控制系统的安全和效率。理解并应用这些分析方法对于控制工程师而言是基本功。
## 2.3 模糊控制的原理与应用
### 2.3.1 模糊控制器的设计
设计一个模糊控制器包括定义模糊集合、模糊规则、模糊推理以及清晰化(defuzzification)过程。设计过程通常遵循以下步骤:
1. **确定输入和输出变量**:首先需要确定控制器需要处理的输入和输出变量,并为每个变量定义相应的模糊集合。
2. **定义隶属函数**:为每个模糊集合定义隶属函数,这些函数确定了变量的隶属度。
3. **建立模糊规则**:基于领域知
0
0






