加权平均法在模糊控制器设计中的关键作用及实践方法


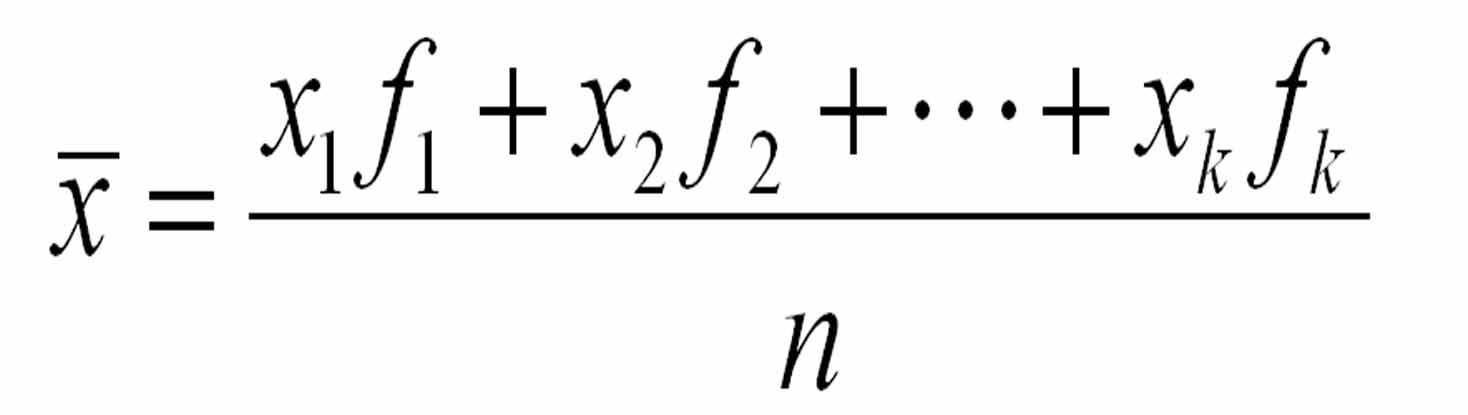
# 摘要
模糊控制器作为一种非线性控制策略，在处理不确定性信息和复杂系统中表现出独特优势。本文首先阐述加权平均法在模糊控制器中的理论基础，探讨了模糊逻辑的关键技术，包括模糊集合、隶属度函数、模糊规则构建及其推理机制。接着，深入分析了加权平均法的原理、数学模型以及其对模糊控制器性能评价的影响。通过具体案例，本文讨论了加权因子的优化方法、模糊控制器的自适应调整以及模拟与测试的重要性。最后，对模糊控制技术的未来发展趋势进行了展望，指出了面临的挑战和研究方向，为相关领域提供了理论支持和实践指导。

# 关键字
模糊控制器；加权平均法；模糊逻辑；隶属度函数；性能评价；自适应调整

参考资源链接：[模糊控制理论详解：加权平均法在模糊系统中的应用](https://wenku.csdn.net/doc/89pmt2n5co?spm=1055.2635.3001.10343)
# 1. 加权平均法在模糊控制器中的理论基础

## 1.1 模糊控制器的概述与历史
模糊控制器作为一种基于模糊逻辑的控制系统，自20世纪80年代提出以来，已成为处理不确定性问题的重要工具。它将传统逻辑的“0”或“1”的二值判断转变为连续的隶属度值，从而在各种复杂场景下提供更贴近人类思维模式的决策支持。加权平均法作为模糊控制器中常用的去模糊化技术，其重要性在于将模糊集合中的信息转换为精确的输出值，以便于执行实际的控制任务。

## 1.2 加权平均法的基本原理
加权平均法依赖于隶属度函数对模糊集合进行赋值，通过为每个模糊集合内的值赋予不同的权重，再通过加权求和的方式，计算出一个精确的控制量。这种方法的关键在于权重的选择和隶属度函数的设计，它们直接影响到控制器的性能和适用性。

## 1.3 理论基础与数学表达
在数学表述中，加权平均法可以表示为一个期望值的计算过程，其中每个模糊集合的隶属度值乘以对应的权重，再除以所有权重的总和。该方法的数学模型能够处理具有不确定性或模糊边界的控制输入，并且能够在精确度和计算复杂度之间提供平衡。

U = \frac{\sum_{i=1}^{n} w_i * \mu_{A_i}(u_i)}{\sum_{i=1}^{n} w_i}

在上述公式中，\(U\) 是去模糊化后的输出值，\(w_i\) 是第 \(i\) 个模糊集合的权重，\(\mu_{A_i}(u_i)\) 表示输入 \(u_i\) 对应模糊集合 \(A_i\) 的隶属度函数值。通过调整权重和隶属度函数，可以实现对模糊控制器输出的精细控制。

# 2. 模糊逻辑基础

### 模糊集合和隶属度函数

在模糊控制器的设计中，首先需要明确的是模糊集合和隶属度函数的概念。在传统的集合论中，一个元素要么完全属于某个集合，要么不属于。而模糊逻辑引入了隶属度的概念，允许一个元素以不同程度属于多个集合。例如，在温度控制系统中，温度可以部分属于“冷”、“正常”或“热”等多个模糊集合，而不是简单地被分类为“冷”或“不冷”。

隶属度函数是描述元素对于模糊集合隶属程度的数学函数。它将每个可能的输入值映射到[0,1]区间内的一个数，其中0表示完全不属于，1表示完全属于。常见的隶属度函数有三角形、梯形、高斯形等。

graph LR
A[输入值] -->|隶属度函数| B[隶属度]
B --> C[隶属程度]
C --> D{温度类别}
D -->|隶属度高| E[冷]
D -->|隶属度中| F[正常]
D -->|隶属度低| G[热]

### 模糊规则的构建和推理机制

模糊规则是模糊控制器的核心，它定义了输入变量与输出变量之间的关系。一个典型的模糊规则可以表示为“如果（输入1是模糊集合A）和（输入2是模糊集合B），那么（输出是模糊集合C）”。例如，在温度控制中，规则可能是“如果温度很高且湿度很高，那么需要很强的冷却”。

模糊推理机制用于根据模糊规则和当前输入计算出模糊输出。常用的方法包括Mamdani和Sugeno方法。Mamdani方法直接输出模糊集合，而Sugeno方法输出的则是模糊集合的函数。模糊推理过程通常包括模糊化、规则应用和去模糊化三个步骤。

graph LR
A[当前输入] --> B[模糊化]
B --> C[规则应用]
C --> D[去模糊化]
D --> E[模糊输出]

去模糊化是将模糊输出转换为具体数值的过程。常用的方法有重心法、最大隶属度法等。重心法通过计算隶属度函数曲线下的面积重心来得到一个清晰的输出值。

在下一节中，我们将深入探讨加权平均法在模糊控制器设计中的原理与数学模型，这是理解和优化模糊控制器性能的关键。

# 3. 加权平均法在模糊控制器设计中的应用

加权平均法是模糊控制领域中用于综合模糊规则输出的一种有效方法。在设计模糊控制器时，如何合理利用加权平均法以提升控制系统的性能，是本章的核心内容。

## 3.1 模糊控制器的加权因子优化

加权因子是模糊控制器中的关键参数，它影响着控制器的输出和性能。对于不同类型的控制问题，适当的加权因子可以改善模糊控制系统的响应特性和鲁棒性。

### 3.1.1 加权因子对控制器性能的影响

加权因子的设计直接关系到模糊控制器的最终输出。在实际应用中，加权因子的值需要根据系统的动态特性和响应要求进行调整。例如，在一些快速响应系统中，可能需要增加控制规则中误差较大项的权重，以此来加快系统的响应速度；而在那些需要高稳定性的系统中，则可能需要相对均匀地分配权重，以避免过调和振荡现象。

### 3.1.2 实际案例中的加权因子优化方法

以一个温度控制系统为例，该系统要求快速达到设定温度并保持稳定。通过实验和调整发现，给予当前温度偏差较大权重、对历史偏差使用较小权重的方法，能够使系统快速反应并具有较好的稳定性。以下是一个简单的权重调整策略的伪代码实现：

# 假设 error 是当前的温度偏差，prev_errors 是历史偏差记录
def calculate_output(error, prev_errors):
    weights = [0.6, 0.3, 0.1]  # 权重列表，根据实际情况调整
    weighted_errors = [error * weights[0]] + [pe * w for pe, w in zip(prev_errors, weights[1:])]
    output = sum(weighted_