单片机舵机控制进阶指南：PID算法与反馈控制，解锁舵机控制新境界

# 1. 舵机控制基础**

舵机是一种广泛应用于机器人、无人机和工业自动化领域的执行器，它能够根据控制信号精确地旋转到指定角度。舵机控制的基础知识对于深入理解PID算法和反馈控制至关重要。

舵机的工作原理是利用电机的转动带动齿轮组，从而改变舵机输出轴的角度。舵机通常通过脉宽调制（PWM）信号进行控制，PWM信号的脉冲宽度决定了舵机旋转的角度。

舵机控制接口通常包括电源、地线和控制信号线。电源为舵机提供工作电压，地线提供参考电位，控制信号线接收PWM信号并控制舵机的旋转。

# 2. PID算法原理与应用

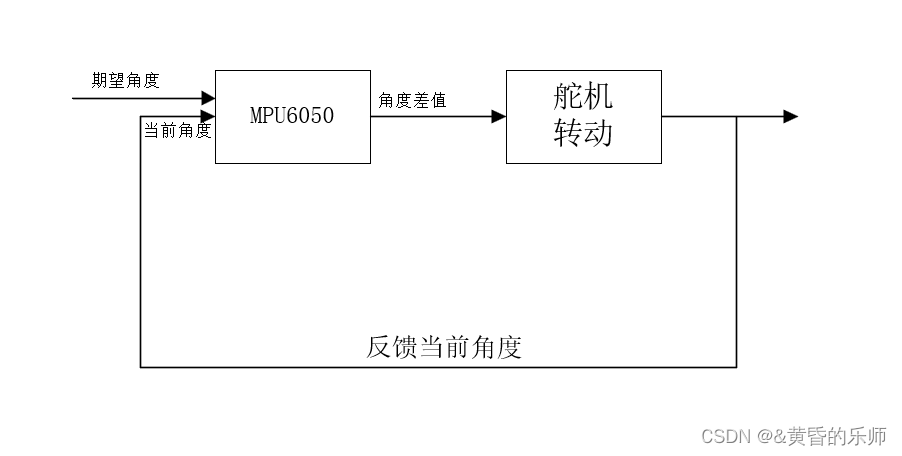
PID算法（比例-积分-微分算法）是一种广泛应用于控制系统的反馈控制算法。它通过测量系统的输出与期望值之间的误差，并根据误差的比例、积分和微分值来调整系统的输入，从而实现系统的稳定性和精度控制。

### 2.1 PID算法的基本原理

PID算法的基本原理是将误差分解为三个部分：比例项（P）、积分项（I）和微分项（D）。

#### 2.1.1 比例项（P）

比例项与误差成正比，即输出与误差的当前值成正比。比例项的目的是快速响应误差的变化，从而减少系统的瞬态误差。但是，比例项过大会导致系统振荡，因此需要适当调整。

#### 2.1.2 积分项（I）

积分项与误差的积分值成正比，即输出与误差的过去值成正比。积分项的目的是消除系统的稳态误差，即当系统达到稳定状态时，误差为零。但是，积分项过大会导致系统反应缓慢，因此需要适当调整。

#### 2.1.3 微分项（D）

微分项与误差的微分值成正比，即输出与误差的变化率成正比。微分项的目的是预测误差的变化，并提前调整系统的输入，从而提高系统的响应速度和稳定性。但是，微分项过大会导致系统噪声放大，因此需要适当调整。

### 2.2 PID算法的调参方法

PID算法的调参是至关重要的，它直接影响系统的性能。常用的调参方法有：

#### 2.2.1 Ziegler-Nichols法

Ziegler-Nichols法是一种基于系统阶跃响应的调参方法。通过测量系统的阶跃响应时间和峰值，可以计算出PID参数的初始值。

#### 2.2.2 试错法

试错法是一种简单但耗时的调参方法。通过反复调整PID参数，观察系统的响应，并根据响应情况调整参数，直至达到满意的效果。

#### 2.2.3 遗传算法

遗传算法是一种基于进化论的调参方法。通过模拟生物进化过程，遗传算法可以自动搜索最优的PID参数。

# PID算法实现

def pid_control(error, kp, ki, kd, dt):
    """
    PID控制算法

    参数：
        error: 误差值
        kp: 比例系数
        ki: 积分系数
        kd: 微分系数
        dt: 采样时间

    返回：
        控制输出
    """

    # 计算比例项
    p = kp * error

    # 计算积分项
    i = ki * dt * error

    # 计算微分项
    d = kd * (error - previous_error) / dt