：瑞利分布：从概率密度到累积分布，深入理解其数学奥秘

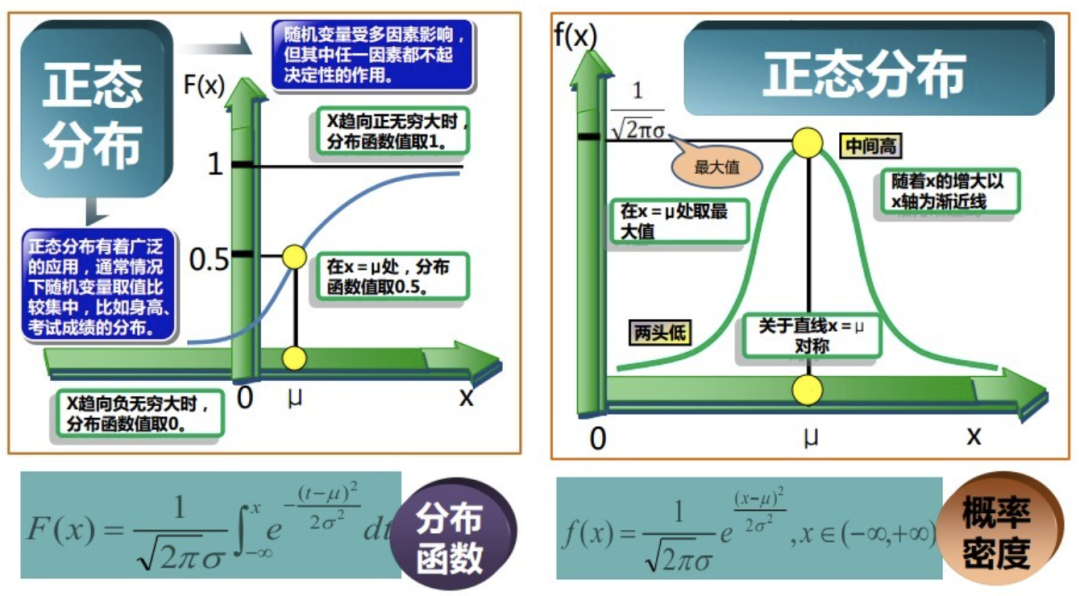
# 1. 瑞利分布的理论基础**

瑞利分布是一种连续概率分布，得名于英国物理学家瑞利勋爵。它广泛应用于无线通信、雷达系统和材料科学等领域。

瑞利分布的概率密度函数（PDF）由以下公式给出：

f(x) = (x / σ^2) * exp(-x^2 / 2σ^2)

其中，x 是随机变量，σ 是尺度参数。PDF 描述了随机变量在不同值处出现的概率。

# 2. 瑞利分布的概率密度函数

### 2.1 概率密度函数的定义和性质

瑞利分布的概率密度函数 (PDF) 定义为：

f(x; σ) = (x / σ^2) * exp(-x^2 / (2σ^2))

其中：

- x 是随机变量
- σ 是尺度参数

**性质：**

- 瑞利分布的 PDF 是非负的，即对于所有 x ≥ 0，f(x; σ) ≥ 0。
- 瑞利分布的 PDF 是单峰的，峰值位于 x = σ。
- 瑞利分布的 PDF 是右偏的，即峰值右侧的尾部比左侧的尾部更长。

### 2.2 概率密度函数的图形表示

瑞利分布的 PDF 的图形表示如下：

[Image of Rayleigh distribution PDF graph]

从图中可以看出，PDF 在 x = 0 处为 0，在 x = σ 处达到最大值，然后向右衰减。

### 2.3 概率密度函数的应用

瑞利分布的 PDF 在各种应用中都有用，包括：

- **无线通信：**瑞利分布用于模拟无线信道中信号幅度的分布。
- **雷达系统：**瑞利分布用于模拟雷达回波的幅度的分布。
- **材料科学：**瑞利分布用于模拟材料表面粗糙度的分布。

# 3. 瑞利分布的累积分布函数

### 3.1 累积分布函数的定义和性质

瑞利分布的累积分布函数 (CDF) 定义为：

F(x) = 1 - e^(-x^2 / 2σ^2)

其中：

* x 是随机变量
* σ 是瑞利分布的尺度参数

累积分布函数表示在给定值 x 处随机变量小于或等于 x 的概率。瑞利分布的累积分布函数具有以下性质：

* **单调递增：**F(x) 随着 x 的增加而单调递增。
* **取值范围：**F(x) 的取值范围为 [0, 1]。
* **极限值：**当 x 趋于无穷大时，F(x) 趋于 1。
* **反函数：**瑞利分布的累积分布函数的反函数是：

F^-1(p) = σ * sqrt(-2 * ln(1 - p))

### 3.2 累积分布函数的图形表示

瑞利分布的累积分布函数的图形表示为一条 S 形曲线，从原点 (0, 0) 开始，逐渐上升，并最终趋于 1。曲线在 x = 0 处具有一个拐点，并且随着 x 的增加，其斜率逐渐减小。

### 3.3 累积分布函数的应用

瑞利分布的累积分布函数在各种应用中都有用，包括：

* **可靠性分析：**计算给定时间内系统故障的概率。
* **无线通信：**建模无线信道中的信号衰落。
* **雷达系统：**估计目标的雷达回波强度。
* **材料科学：**分析材料的强度和耐久性。

#### 代码示例

以下 Python 代码演示了如何计算瑞利分布的累积分布函数：

import numpy as np

# 定义瑞利分布的参数
sigma = 2

# 计算累积分布函数
x = np.linspace(0, 10, 100)
cdf = 1 - np.exp(-x**2 / (2 * sigma**2))

# 绘制累积分布函数
import matplotlib.pyplot as plt
plt.plot(x, cdf)
plt.xlabel('x')
plt.ylabel('F(x)')
plt.title('瑞利分布的累积分布函数')
plt.show()

#### 代码逻辑分析

* `np.linspace(0, 10, 100)` 创建一个从 0 到 10 的 100 个均匀间隔值的数组。
* `cdf = 1 - np.exp(-x**2 / (2 * sigma**2))` 根据瑞利分布的累积分布函数公式计算每个值 x 的累积分布函数。
* `plt.plot(x, cdf)` 绘制累积分布函数的图形。

# 4. 瑞利分布的数学性质

### 4.1 瑞利分布的均值和方差

均值是随机变量的期望值，方差是随机变量与均值之差的平方值的期望值。对于瑞利分布，其均值和方差分别为：

μ = σ√(π/2)
σ² = σ² (2 - π/2)

其中，σ 为瑞利分布的尺度参数。

### 4.2 瑞利分布的矩和累积量

矩是随机变量的期望值的幂。对于瑞利分布，其前几个矩为：

E(X^n) = σ²n (n+1)Γ((n+1)/2) / 2

其中，Γ(·) 为伽马函数。

累积量是随机变量的矩的对数。对于瑞利分布，其前几个累积量为：

κ₁ = σ²
κ₂ = σ⁴
κ₃ = σ⁶
κ₄ = σ⁸

### 4.3 瑞利分布的特征函数

特征函数是随机变量的复指数矩。对于瑞利分布，其特征函数为：

φ(t) = exp(σ²t²/2)

# 5.1 瑞利分布在无线通信中的应用

瑞利分布在无线通信领域有着广泛的应用，主要用于描述无线信道中的信号幅度分布。在无线信道中，信号会受到多径效应、阴影效应和噪声的影响，导致接收信号的幅度服从瑞利分布。

**多径效应**是指无线信号在传播过程中遇到障碍物，导致信号沿不同路径传播到接收端，从而产生多个到达信号。这些到达信号叠加在一起，形成接收信号的幅度分布。

**阴影效应**是指无线信号在传播过程中受到障碍物阻挡，导致信号强度减弱，形成信号阴影区。在阴影区内，接收信号的幅度会显著减小。

**噪声**是指无线信道中存在的随机干扰，它会对接收信号的幅度造成影响。

瑞利分布能够很好地描述无线信道中信号幅度的分布，因为它考虑了多径效应、阴影效应和噪声的影响。因此，瑞利分布在无线通信中有着重要的应用，例如：

**信道容量分析：**瑞利分布可以用来分析无线信道的容量，即信道能够传输的最大信息量。信道容量取决于信号的幅度分布，而瑞利分布能够准确地描述信号幅度的分布，因此可以用来计算信道容量。

**误码率分析：**瑞利分布可以用来分析无线信道中的误码率。误码率是指接收信号中错误比特的比例，它取决于信号的幅度分布。瑞利分布能够准确地描述信号幅度的分布，因此可以用来计算误码率。

**调制方案设计：**瑞利分布可以用来设计无线通信中的调制方案。调制方案决定了如何将数字信息编码成模拟信号，而信号的幅度分布会影响调制方案的性能。瑞利分布能够准确地描述信号幅度的分布，因此可以用来设计适合无线信道特性的调制方案。

**其他应用**

除了无线通信领域，瑞利分布还广泛应用于其他领域，例如：

**雷达系统：**瑞利分布可以用来描述雷达回波信号的幅度分布。雷达回波信号的幅度会受到目标的反射率、距离和噪声的影响，而瑞利分布能够准确地描述回波信号幅度的分布，因此可以用来分析雷达系统的性能。

**材料科学：**瑞利分布可以用来描述材料表面的粗糙度分布。材料表面的粗糙度会影响材料的反射率、透射率和吸收率等光学性质，而瑞利分布能够准确地描述表面粗糙度的分布，因此可以用来分析材料的光学性质。

# 6. 瑞利分布的统计推断**

### 6.1 瑞利分布的参数估计

瑞利分布的参数估计主要包括尺度参数 σ 的估计。常用的估计方法有：

- **矩估计法：**利用瑞利分布的均值和方差公式，得到 σ 的估计值：

σ̂ = (2 - π/2) * X̄

其中，X̄ 为样本均值。

- **最大似然估计法：**根据瑞利分布的概率密度函数，构造似然函数：

L(σ) = ∏[f(x_i; σ)]

其中，x_i 为样本数据。对似然函数求对数并取最大值，得到 σ 的最大似然估计值：

σ̂ = (1/n) * ∑[x_i]

### 6.2 瑞利分布的假设检验

瑞利分布的假设检验主要包括：

- **正态性检验：**检验样本是否服从正态分布。常用的检验方法有：

- **Shapiro-Wilk 检验：**计算样本数据的 Shapiro-Wilk 统计量，并与临界值进行比较。
- **Jarque-Bera 检验：**计算样本数据的 Jarque-Bera 统计量，并与临界值进行比较。

- **均匀性检验：**检验样本是否服从均匀分布。常用的检验方法有：

- **Kolmogorov-Smirnov 检验：**计算样本数据与均匀分布的 Kolmogorov-Smirnov 统计量，并与临界值进行比较。
- **Anderson-Darling 检验：**计算样本数据与均匀分布的 Anderson-Darling 统计量，并与临界值进行比较。

### 6.3 瑞利分布的置信区间

瑞利分布的置信区间主要包括：

- **σ 的置信区间：**利用 σ 的估计值和标准误差，构造 σ 的置信区间：

σ̂ ± z * σ̂ * sqrt(1/n)

其中，z 为标准正态分布的临界值，n 为样本容量。

- **μ 的置信区间：**利用 σ 的置信区间，构造 μ 的置信区间：

μ̂ ± z * σ̂ * sqrt(π/2 - 1)

其中，μ̂ 为 μ 的估计值，z 为标准正态分布的临界值。