【Matlab坐标轴秘籍】：15个技巧助你轻松掌控坐标轴

# 1. Matlab坐标轴概述

坐标轴是Matlab中用于绘制图形的基本元素之一。它定义了数据点的空间位置，并提供了对图形的视觉参考。Matlab提供了广泛的选项来定制坐标轴的外观和行为，以满足各种绘图需求。

坐标轴由水平x轴和垂直y轴组成，它们相交于原点。坐标轴的范围定义了数据点可以绘制的区域，而刻度则提供间隔以帮助解释数据。坐标轴还可以包含标签和标题，以提供有关图形的附加信息。

# 2. 坐标轴属性设置

坐标轴属性设置是自定义坐标轴外观和行为的关键部分。Matlab 提供了各种属性，允许您控制坐标轴的范围、刻度、标签、标题、网格和背景。

### 2.1 坐标轴范围和刻度

#### 2.1.1 设置坐标轴范围

坐标轴范围定义了坐标轴上数据点的最小值和最大值。您可以使用 `axis` 函数设置坐标轴范围。语法如下：

axis([xmin xmax ymin ymax])

其中，`xmin` 和 `xmax` 指定 x 轴的最小值和最大值，`ymin` 和 `ymax` 指定 y 轴的最小值和最大值。

**代码块：**

% 设置 x 轴范围为 [0, 10]
axis([0 10 0 10])

% 设置 y 轴范围为 [-5, 5]
axis([0 10 -5 5])

**逻辑分析：**

* 第一个代码块将 x 轴范围设置为 [0, 10]，y 轴范围设置为 [0, 10]。
* 第二个代码块将 x 轴范围保持不变，将 y 轴范围设置为 [-5, 5]。

#### 2.1.2 设置坐标轴刻度

坐标轴刻度定义了坐标轴上显示的刻度线和刻度标签。您可以使用 `set` 函数设置坐标轴刻度。语法如下：

set(gca, 'XTick', [x1 x2 ...])
set(gca, 'YTick', [y1 y2 ...])

其中，`gca` 获取当前坐标轴句柄，`XTick` 和 `YTick` 指定 x 轴和 y 轴的刻度值。

**代码块：**

% 设置 x 轴刻度为 [0, 2, 4, 6, 8, 10]
set(gca, 'XTick', [0 2 4 6 8 10])

% 设置 y 轴刻度为 [-5, -2, 0, 2, 5]
set(gca, 'YTick', [-5 -2 0 2 5])

**逻辑分析：**

* 第一个代码块将 x 轴刻度设置为 [0, 2, 4, 6, 8, 10]。
* 第二个代码块将 y 轴刻度设置为 [-5, -2, 0, 2, 5]。

### 2.2 坐标轴标签和标题

#### 2.2.1 设置坐标轴标签

坐标轴标签是坐标轴上显示的刻度线旁边的文本。您可以使用 `xlabel` 和 `ylabel` 函数设置坐标轴标签。语法如下：

xlabel('X-Axis Label')
ylabel('Y-Axis Label')

其中，`xlabel` 和 `ylabel` 指定 x 轴和 y 轴的标签文本。

**代码块：**

% 设置 x 轴标签为 "Time (s)"
xlabel('Time (s)')

% 设置 y 轴标签为 "Amplitude (V)"
ylabel('Amplitude (V)')

**逻辑分析：**

* 第一个代码块将 x 轴标签设置为 "Time (s)"。
* 第二个代码块将 y 轴标签设置为 "Amplitude (V)"。

#### 2.2.2 设置坐标轴标题

坐标轴标题是坐标轴上显示的文本，用于描述坐标轴的内容。您可以使用 `title` 函数设置坐标轴标题。语法如下：

title('Plot 

# 3.1 线性变换

线性变换是坐标轴变换中最基本的一种，它可以将坐标轴沿x轴或y轴进行平移或缩放。

#### 3.1.1 平移坐标轴

平移坐标轴是指将坐标轴沿x轴或y轴移动一定距离。可以使用`xlim`和`ylim`函数来设置坐标轴的范围，从而实现平移。

% 创建一个坐标轴
figure;
plot(1:10, rand(1, 10));

% 平移坐标轴
xlim([0, 12]);
ylim([0, 1.5]);

**代码逻辑分析：**

* `plot(1:10, rand(1, 10))`：绘制一条包含10个随机数的折线图。
* `xlim([0, 12])`：将x轴范围设置为[0, 12]，将坐标轴沿x轴向右平移2个单位。
* `ylim([0, 1.5])`：将y轴范围设置为[0, 1.5]，将坐标轴沿y轴向上平移0.5个单位。

#### 3.1.2 缩放坐标轴

缩放坐标轴是指将坐标轴沿x轴或y轴放大或缩小一定倍数。可以使用`daspect`函数来设置坐标轴的纵横比，从而实现缩放。

% 创建一个坐标轴
figure;
plot(1:10, rand(1, 10));

% 缩放坐标轴
daspect([2 1 1]);

**代码逻辑分析：**

* `plot(1:10, rand(1, 10))`：绘制一条包含10个随机数的折线图。
* `daspect([2 1 1])`：将坐标轴的纵横比设置为[2 1 1]，将x轴放大2倍，y轴保持不变。

### 3.2 对数变换

对数变换是一种非线性变换，它可以将数据分布在不同的尺度上，从而更清晰地显示数据之间的关系。

#### 3.2.1 对数坐标轴的创建

可以使用`loglog`函数来创建对数坐标轴。

% 创建一个对数坐标轴
figure;
loglog(1:10, rand(1, 10));

**代码逻辑分析：**

* `loglog(1:10, rand(1, 10))`：绘制一条包含10个随机数的对数坐标轴折线图。

#### 3.2.2 对数坐标轴的属性设置

对数坐标轴的属性可以通过`set`函数进行设置。

% 创建一个对数坐标轴
figure;
loglog(1:10, rand(1, 10));

% 设置对数坐标轴的属性
set(gca, 'XScale', 'log', 'YScale', 'log');

**代码逻辑分析：**

* `loglog(1:10, rand(1, 10))`：绘制一条包含10个随机数的对数坐标轴折线图。
* `set(gca, 'XScale', 'log', 'YScale', 'log')`：将x轴和y轴的刻度都设置为对数刻度。

# 4. 坐标轴注解

坐标轴注解是用于在坐标轴上添加附加信息的元素。这些注解可以是文本、图形或两者兼有。

### 4.1 文本注解

#### 4.1.1 添加文本注解

要添加文本注解，可以使用 `text` 函数。该函数的语法如下：

text(x, y, str, 'PropertyName', PropertyValue, ...)

其中：

* `x` 和 `y` 指定注解的位置。
* `str` 是要显示的文本。
* `'PropertyName'` 和 `PropertyValue` 是可选的属性值对，用于设置注解的属性。

例如，以下代码在坐标轴上添加一个文本注解：

text(10, 20, '文本注解', 'Color', 'red', 'FontSize', 14);

这将创建一个红色的文本注解，字体大小为 14，位于 `x = 10` 和 `y = 20` 的位置。

#### 4.1.2 设置文本注解属性

文本注解的属性可以通过 `'PropertyName'` 和 `PropertyValue` 参数进行设置。一些常用的属性包括：

* `'Color'`：设置文本颜色。
* `'FontSize'`：设置文本字体大小。
* `'FontName'`：设置文本字体。
* `'HorizontalAlignment'`：设置文本水平对齐方式。
* `'VerticalAlignment'`：设置文本垂直对齐方式。

### 4.2 图形注解

#### 4.2.1 添加图形注解

要添加图形注解，可以使用 `line`、`rectangle` 或 `circle` 等函数。这些函数的语法如下：

line(x, y, 'PropertyName', PropertyValue, ...)
rectangle('Position', [x, y, width, height], 'PropertyName', PropertyValue, ...)
circle('Center', [x, y], 'Radius', radius, 'PropertyName', PropertyValue, ...)

其中：

* `x` 和 `y` 指定图形的位置。
* `'PropertyName'` 和 `PropertyValue` 是可选的属性值对，用于设置图形的属性。

例如，以下代码在坐标轴上添加一个矩形注解：

rectangle('Position', [10, 20, 50, 30], 'FaceColor', 'blue', 'EdgeColor', 'red');

这将创建一个蓝色填充、红色边框的矩形注解，位于 `x = 10`、`y = 20` 的位置，宽度为 50，高度为 30。

#### 4.2.2 设置图形注解属性

图形注解的属性可以通过 `'PropertyName'` 和 `PropertyValue` 参数进行设置。一些常用的属性包括：

* `'FaceColor'`：设置填充颜色。
* `'EdgeColor'`：设置边框颜色。
* `'LineWidth'`：设置边框宽度。
* `'LineStyle'`：设置边框样式。
* `'Marker'`：设置标记类型。
* `'MarkerSize'`：设置标记大小。

# 5. 坐标轴布局

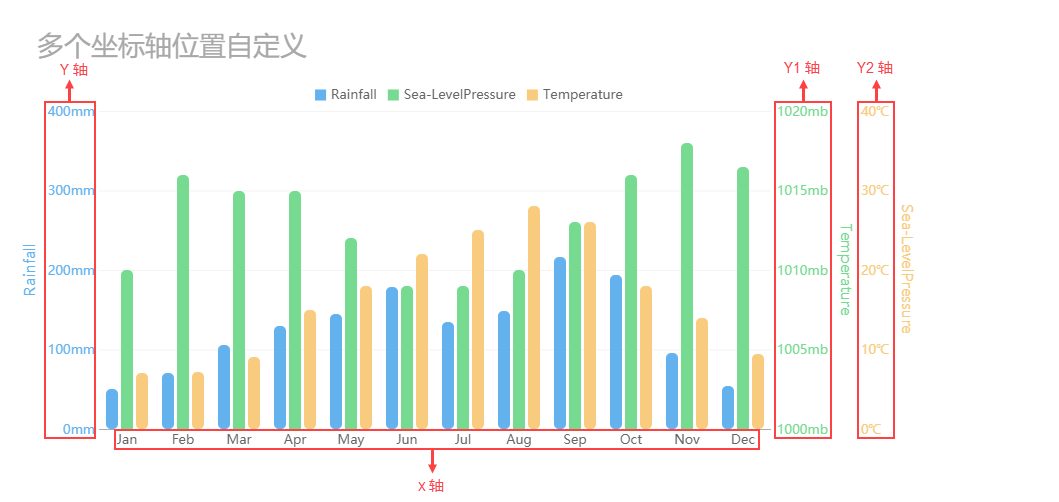
### 5.1 多个坐标轴

#### 5.1.1 创建多个坐标轴

在同一图形中创建多个坐标轴可以实现将不同的数据集或信息可视化在不同的坐标系中。Matlab 提供了 `subplot` 函数来创建多个坐标轴。`subplot` 函数的语法如下：

subplot(m, n, p)

其中：

* `m`：指定图形中子图的行数。
* `n`：指定图形中子图的列数。
* `p`：指定当前子图在图形中的位置。

例如，要创建包含两个子图的图形，其中第一个子图位于第一行第一列，第二个子图位于第一行第二列，可以使用以下代码：

subplot(1, 2, 1);
subplot(1, 2, 2);

#### 5.1.2 协调多个坐标轴

当创建多个坐标轴时，可能需要协调它们以确保它们具有相同的比例或范围。Matlab 提供了 `linkaxes` 函数来协调坐标轴。`linkaxes` 函数的语法如下：

linkaxes(axes_array, 'property')

其中：

* `axes_array`：要协调的坐标轴数组。
* `property`：要协调的属性，例如 `'xlims'`、`'ylims'` 或 `'view'`。

例如，要将两个坐标轴的 x 轴范围链接在一起，可以使用以下代码：

linkaxes([ax1, ax2], 'xlims');

### 5.2 子坐标轴

#### 5.2.1 创建子坐标轴

子坐标轴是嵌套在主坐标轴内的较小的坐标轴。它们通常用于显示与主坐标轴相关但具有不同范围或刻度的信息。Matlab 提供了 `axes` 函数来创建子坐标轴。`axes` 函数的语法如下：

axes('Position', [left, bottom, width, height])

其中：

* `Position`：子坐标轴的位置和大小，指定为 `[left, bottom, width, height]`，其中 `left` 和 `bottom` 是子坐标轴左下角的相对位置，`width` 和 `height` 是子坐标轴的宽度和高度。

例如，要在主坐标轴的右上角创建一个子坐标轴，可以使用以下代码：

axes('Position', [0.6, 0.6, 0.3, 0.3]);

#### 5.2.2 设置子坐标轴属性

子坐标轴具有与主坐标轴相同的属性，可以对其进行设置以自定义其外观和行为。可以使用与主坐标轴相同的函数和方法来设置子坐标轴的属性。

例如，要设置子坐标轴的标题，可以使用以下代码：

title('子坐标轴标题');

# 6.1 坐标轴事件处理

### 6.1.1 响应坐标轴事件

Matlab 提供了多种事件，可以用来响应坐标轴上的用户交互。这些事件包括：

- `ButtonDownFcn`：当鼠标在坐标轴上按下时触发。
- `ButtonUpFcn`：当鼠标在坐标轴上释放时触发。
- `WindowButtonDownFcn`：当鼠标在坐标轴的窗口中按下时触发。
- `WindowButtonUpFcn`：当鼠标在坐标轴的窗口中释放时触发。
- `WindowButtonMotionFcn`：当鼠标在坐标轴的窗口中移动时触发。

要响应这些事件，可以使用 `set` 函数将事件处理函数分配给相应的事件属性。例如，要响应鼠标在坐标轴上按下的事件，可以使用以下代码：

set(gca, 'ButtonDownFcn', @myButtonDownFcn);

其中，`myButtonDownFcn` 是一个自定义的事件处理函数。

### 6.1.2 自定义坐标轴事件处理函数

自定义坐标轴事件处理函数必须是接受一个事件对象作为输入参数的函数。事件对象包含有关触发事件的信息，例如鼠标位置和按钮状态。

以下是一个自定义坐标轴事件处理函数的示例，它在鼠标在坐标轴上按下时打印鼠标位置：

function myButtonDownFcn(hObject, eventdata)
% 获取鼠标位置
mousePosition = get(gca, 'CurrentPoint');
% 打印鼠标位置
disp(['鼠标位置：', num2str(mousePosition(1)), ', ', num2str(mousePosition(2))]);
end

要使用自定义事件处理函数，请将其分配给相应的事件属性，如上所示。