Java算法优化大揭秘：动态规划与递归解题技巧，让代码飞起来

# 1. 算法优化的基本概念与重要性

## 算法优化的基本概念

在信息科技领域，算法优化指的是对现有算法进行改进，以期在时间复杂度、空间复杂度或者资源消耗上实现更高效的性能。优化可以涉及算法设计的各个环节，包括但不限于问题的分解、数据结构的选择、代码层面的改进和算法的数学建模。优化的目标是减少算法的执行时间、减少所需存储空间或两者兼具。

## 算法优化的重要性

在实际的软件开发和应用中，算法优化扮演着至关重要的角色。一方面，它能够显著提高程序运行效率，减少资源占用，提升用户体验。另一方面，优化可以降低系统运营成本，尤其在大数据处理、实时系统和云计算等资源敏感的环境中至关重要。此外，算法优化对于解决复杂的计算问题，如图论、数值分析等，具有不可替代的作用。因此，深入理解和掌握算法优化的策略和方法，对于IT行业的专业人士来说，是一项基本且必备的技能。

# 2. 动态规划原理与实现

## 2.1 动态规划的基本理论

### 2.1.1 动态规划的定义和原理

动态规划是解决多阶段决策过程优化问题的一种方法。它将复杂问题分解为简单的子问题，通过解决这些子问题，逐步推导出整个问题的最优解。动态规划通常适用于有重叠子问题和最优子结构的场景，重叠子问题意味着在问题的递归解法中，相同的小问题多次求解，而最优子结构意味着问题的最优解包含其子问题的最优解。

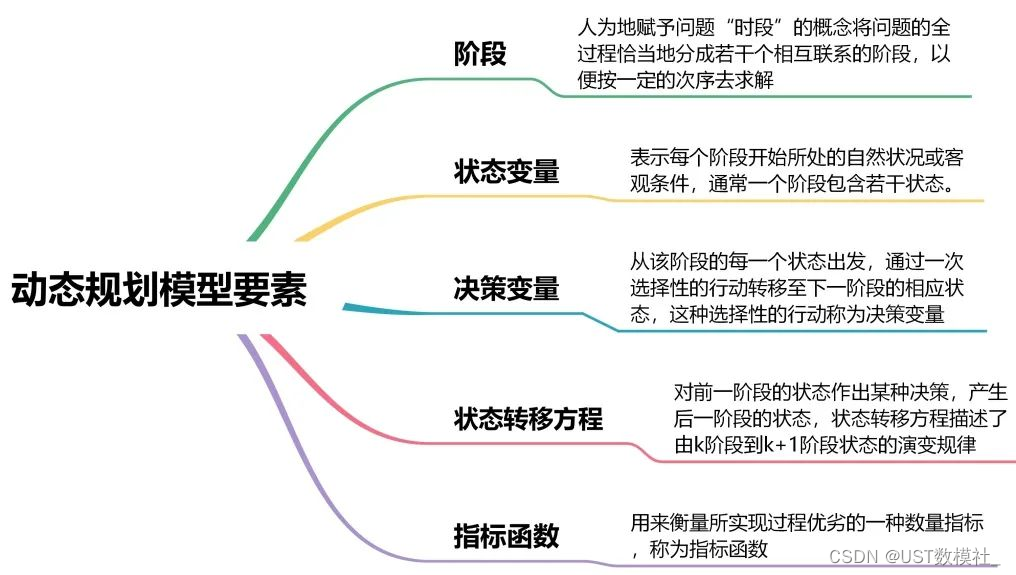
动态规划的核心在于将问题划分成阶段，每个阶段包含一组状态，状态之间通过决策互相转移。决策的最终目的是要达到最优的状态组合，即全局最优解。动态规划通过构建一个表格来存储子问题的解，避免重复计算，提高效率。

### 2.1.2 动态规划与递归的关系

动态规划与递归有着密切的关系，很多动态规划问题都可以使用递归的方式来表达。递归是一种自然的将问题分解为更小相似问题的方法，而动态规划则在此基础上加入了存储子问题解的机制，从而达到优化的目的。

在递归解法中，重复计算是不可避免的，而动态规划通过使用表格法或记忆化搜索技术，存储已经计算过的子问题解，从而避免了重复的计算过程。这种优化手段使得动态规划在时间复杂度上通常优于纯递归方法。

## 2.2 动态规划问题的分解与求解

### 2.2.1 状态定义与转移方程

动态规划问题求解的第一步是定义状态。状态通常用数组表示，数组的每个元素对应问题的一个阶段或子问题的解。状态的定义需要全面覆盖问题的所有可能性，并且能够通过状态之间的转移得到最终解。

状态转移方程是动态规划中解决问题的关键，它描述了状态之间的相互转换关系。方程通常采用递推的形式，即下一个状态的值是如何由前一个或几个状态的值决定的。正确建立状态转移方程是解决动态规划问题的核心，也是难点所在。

### 2.2.2 边界条件和初始值设定

在动态规划中，除了状态转移方程，还需要设定边界条件和初始值。边界条件指明了递归求解的起点，而初始值则是动态规划表中的起始元素。它们为状态转移提供了基础，是计算其他所有状态所依赖的基本情况。

边界条件和初始值的设定要准确无误，否则会导致计算结果错误。在很多情况下，边界条件和初始值的设定可以直观地从问题的定义中得出。例如，在求解最长公共子序列问题时，初始值通常设置为0，因为长度为0的序列的最长公共子序列的长度也是0。

### 2.2.3 优化策略：记忆化搜索与表格法

动态规划的一个关键优化策略是记忆化搜索。记忆化搜索是递归方法的改进，它通过缓存已经计算过的子问题的结果来避免重复计算，这实际上与动态规划的表格法是等价的。在实际操作中，记忆化搜索可以使得递归程序的空间复杂度降至O(n)，而不是传统的递归方法的O(2^n)。

表格法是动态规划的另一种形式，它通常采用一维或多维数组来存储子问题的解。这种方法直观且易于实现，尤其是在问题具有自然的线性结构时。例如，在计算斐波那契数列时，我们可以使用一维数组`dp[]`，其中`dp[i]`表示第`i`个斐波那契数的值。

### 代码示例：斐波那契数列的动态规划实现

public int fibonacci(int n) {
    if (n <= 1) {
        return n;
    }
    int[] dp = new int[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    for (int i = 2; i <= n; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[n];
}

在上述代码中，我们使用了一个一维数组`dp[]`来存储斐波那契数列的值，数组的每个元素对应一个子问题的解。数组的第一个元素`dp[0]`和第二个元素`dp[1]`是初始值，分别对应斐波那契数列的前两个数。之后的元素通过状态转移方程计算得到。

## 2.3 动态规划经典案例分析

### 2.3.1 斐波那契数列问题

斐波那契数列问题是最简单的动态规划示例之一。斐波那契数列定义如下：F(0)=0, F(1)=1, 对于n>1, F(n)=F(n-1)+F(n-2)。问题的目标是计算第n个斐波那契数。

动态规划解法的关键在于定义状态和状态转移方程。在这个问题中，状态`dp[i]`表示第`i`个斐波那契数的值。状态转移方程为：`dp[i] = dp[i - 1] + dp[i - 2]`。初始值为`dp[0] = 0`和`dp[1] = 1`。

代码实现如前所示，通过构建一个数组来存储已计算的斐波那契数，从而避免了重复计算。

### 2.3.2 背包问题

背包问题是一类组合优化的问题。问题的描述是：给定一组物品，每种物品都有自己的重量和价值，在限定的总重量内，如何选择装入背包的物品，使得背包中的物品总价值最大。

对于背包问题，可以定义状态`dp[i][w]`表示对于前`i`个物品，在不超过重量`w`的情况下，能够获得的最大价值。状态转移方程依赖于当前物品重量和价值，以及是否选择当前物品。

- 如果当前物品重量超过`w`，则不选择当前物品，`dp[i][w] = dp[i-1][w]`。
- 如果可以装入当前物品，则有两种选择：装入或不装入当前物品，取两者的较大值，`dp[i][w] = max(dp[i-1][w], dp[i-1][w-weight[i]] + value[i])`。

### 2.3.3 最长公共子序列问题

最长公共子序列（LCS）问题的目标是找出两个序列最长的公共子序列。这个问题可以使用动态规划方法高效地解决。

对于两个序列`X = {x1, x2, ..., xm}`和`Y = {y1, y2, ..., yn}`，定义状态`dp[i][j]`表示`X`的前`i`个字符和`Y`的前`j`个字符的最长公共子序列的长度。状态转移方程如下：

- 如果`xi == yj`，那么`dp[i][j] = dp[i-1][j-1] + 1`。
- 如果`xi != yj`，那么`dp[i][j] = max(dp[i-1][j], dp[i][j-1])`。

通过构建一个二维数组来存储所有子问题的解，可以得到原问题的最优解。

### 表格法示例：最长公共子序列的动态规划实现

public int longestCommonSubsequence(String text1, String text2) {
    int m = text1.length();
    int n = text2.length();
    int[][] dp = new int[m + 1][n + 1];
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    return dp[m][n];
}

在这个示例中，我们使用了一个二维数组`dp[][]`来存储子问题的解。`dp[i][j]`代表`text1`的前`i`个字符和`text2`的前`j`个字符的最长公共子序列的长度。通过填充表格，我们最终获得`dp[m][n]`的值，即为两个字符串的最长公共子序列的长度。

通过上述的案例分析，我们可以看出动态规划方法的强大之处。通过将复杂问题拆解为简单子问题，结合状态定义、状态转移方程以及适当的存储策略，动态规划不仅能够解决经典的算法问题，还为处理实际问题提供了有效的工具和思路。

# 3. 递归算法的优化技巧

递归算法是一种常见的编程技巧，它将问题分解为更小的子问题，直到达到基本情况。然而，递归可能会导致性能问