【高级数据结构】

# 1. 高级数据结构概述

在计算机科学中，数据结构是组织和存储数据的方式，以便能够高效地进行访问和修改。随着技术的发展，尤其是在处理大量数据的应用中，传统的线性数据结构已经不能满足所有需求。因此，高级数据结构应运而生，它们提供了在特定场景下更加高效的数据操作方法。

高级数据结构包括但不限于树型结构、图结构、散列表等，它们各自拥有独特的特点和应用场景。这些数据结构为解决复杂问题提供了更加强大的工具，如树型结构在数据库索引中的运用、图在网络分析中的应用、散列表在快速查找和数据缓存系统中的应用等。

在本章中，我们将探讨这些高级数据结构的基本概念和它们在算法设计中的重要性。接下来的章节将分别深入探讨每一种数据结构的内部机制、操作方法及其在实际应用中的优化策略。理解这些高级数据结构对于任何一名希望在IT领域取得进步的从业者来说都是不可或缺的。

# 2. 树型数据结构

### 2.1 树的基本概念

#### 2.1.1 树的定义和术语

树（Tree）是一种非线性数据结构，它模拟了一种层次结构的抽象。在树结构中，每一个节点可以有零个或多个子节点，这些子节点被称作“叶子节点”或“分支节点”。树的最顶端节点称为根节点（Root），每个非根节点有且仅有一个父节点（Parent），而根节点没有父节点。树中的节点之间存在从上至下的层级关系。

术语解释：

- **节点（Node）**：树结构中的基本单元，包含数据和指向子节点的指针。
- **边（Edge）**：连接两个节点的线段，表示节点之间的父子关系。
- **深度（Depth）**：节点到根节点的唯一路径上的边数。
- **高度（Height）**：节点到最远叶子节点的最长路径上的边数。

与线性数据结构（如链表、数组）相比，树型数据结构特别适合表示层次关系的数据，如组织结构、文件系统等。通过树的层级结构，我们可以快速定位、管理和查询数据。

#### 2.1.2 二叉树和其特殊形式

二叉树（Binary Tree）是最常见的一种树型数据结构，每个节点最多有两个子节点，通常称为左子节点和右子节点。二叉树的特殊形式包括：

- **满二叉树（Full Binary Tree）**：每一个节点都有0个或者2个子节点。
- **完全二叉树（Complete Binary Tree）**：除了最后一层外，其他每一层都被完全填满，且最后一层的节点都靠左排列。
- **二叉搜索树（Binary Search Tree, BST）**：树中的每个节点都满足对于任一节点，其左子树的所有元素都小于该节点，而其右子树的所有元素都大于该节点。

二叉树及其特殊形式在算法和数据结构中极为重要，它们在快速查找、排序和删除等操作上都表现出了优异的性能。

### 2.2 树的操作与应用

#### 2.2.1 树的遍历算法

树的遍历是指按照一定的顺序访问树中的每一个节点，不重复访问任何一个节点。树的遍历算法通常分为三种类型：

- **前序遍历（Pre-order Traversal）**：先访问根节点，然后前序遍历左子树，接着前序遍历右子树。
- **中序遍历（In-order Traversal）**：先中序遍历左子树，然后访问根节点，最后中序遍历右子树。
- **后序遍历（Post-order Traversal）**：先后序遍历左子树，然后后序遍历右子树，最后访问根节点。

中序遍历一个二叉搜索树会得到一个有序序列，这对于排序和查找操作非常有用。

# 中序遍历二叉树的递归函数示例

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right

def inorderTraversal(root):
    if root:
        inorderTraversal(root.left)
        print(root.value)
        inorderTraversal(root.right)

# 示例树结构
#     1
#    / \
#   2   3
#  / \
# 4   5
root = TreeNode(1, TreeNode(2, TreeNode(4), TreeNode(5)), TreeNode(3))
inorderTraversal(root)
# 输出: 4 2 5 1 3

#### 2.2.2 堆和优先队列的实现

堆（Heap）是一种特殊的完全二叉树，通常实现为数组。堆分为两类：最大堆和最小堆。在最大堆中，父节点的值总是大于或等于任何子节点的值；在最小堆中，父节点的值总是小于或等于其子节点的值。

堆是一种优先队列的实现方式，其中最大堆实现最大优先队列，最小堆实现最小优先队列。优先队列是允许在队列中的元素有不同优先级的数据结构，在高优先级元素总是先出队列。

# 最大堆的实现

import heapq

def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1
    r = 2 * i + 2
    if l < n and arr[i] < arr[l]:
        largest = l
    if r < n and arr[largest] < arr[r]:
        largest = r
    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

def maxHeap(arr):
    n = len(arr)
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

# 示例数组
arr = [12, 11, 13, 5, 6, 7]
maxHeap(arr)
print("Maximum element is", arr[0])
# 输出: Maximum element is 13

### 2.3 平衡树和B树

#### 2.3.1 AVL树和红黑树的原理与应用

AVL树和红黑树都是自平衡二叉搜索树。它们通过旋转操作来保持树的平衡，从而保证各种操作（如查找、插入、删除）的效率。

- **AVL树**：任何节点的两个子树的高度最多相差1，如果超过则进行旋转。
- **红黑树**：树上的节点必须是红色或黑色，并且必须满足五个性质：
1. 每个节点是红色或黑色；
2. 根节点是黑色；
3. 每个叶子节点（NIL节点，空节点）是黑色的；
4. 如果一个节点是红色的，则它的两个子节点都是黑色的（从每个叶子到根的所有路径上不能有两个连续的红色节点）；
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

AVL树提供了更严格的平衡条件，因此查询效率更高，但插入和删除操作可能需要更多的调整。红黑树则在插入和删除操作中提供更好的性能，但查询效率略低。红黑树广泛应用于C++ STL中的`map`和`set`，以及Java的`TreeMap`和`TreeSet`中。

// AVL树节点结构的简化版代码

struct AVLNode {
    int key;
    int height;
    AVLNode *left;
    AVLNode *right;
    AVLNode(int k) : key(k), height(1), left(nullptr), right(nullptr) {}
};

// 红黑树节点结构的简化版代码

enum NodeColor {
    RED,
    BLACK
};

struct RBTreeNode {
    int key;
    NodeColor color;
    RBTreeNode *left;
    RBTreeNode *right;
    RBTreeNode *parent;
    RBTreeNode(int k) : key(k), color(RED), left(nullptr), right(nullptr), parent(nullptr) {}
};

#### 2.3.2 B树和B+树在数据库索引中的应用

B树和B+树是多路平衡查找树，非常适合用于读写相对较大的数据块的系统，例如磁盘存储系统。B树的每一个节点可以有多个子节点，能够减少磁盘I/O次数，提高数据检索的速度。

- **B树**：具有以下特点：
1. 所有的键值分布在整棵树中；
2. 每个节点最多包含m个子节点；
3. 根节点最少有两个子节点；
4. 非根节点最少有`ceil(m/2)`个子节点；
5. 每个节点的键值从左至右有序排列，其中节点内的键值可以重复。

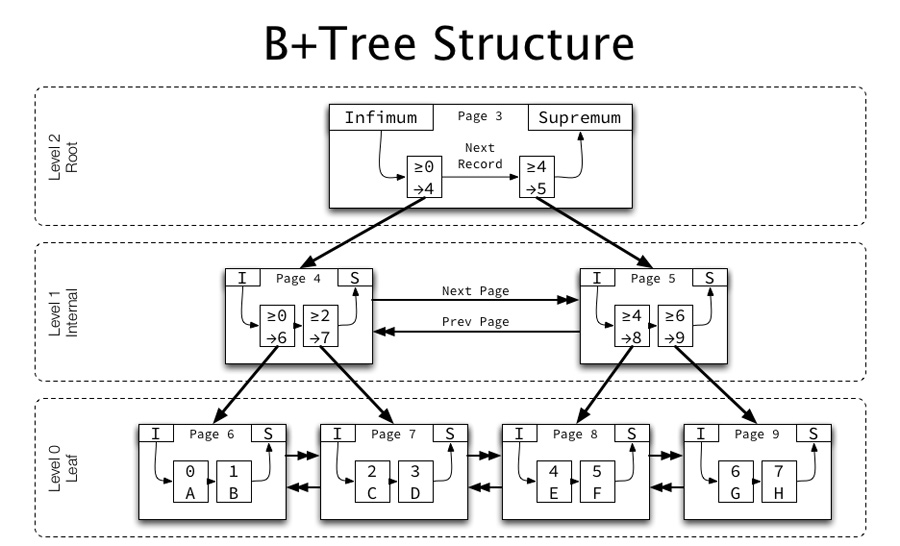
- **B+树**：是B树的变种，它与B树的不同点在于：
1. 所有的数据记录都存放在叶子节点；
2. 非叶子节点仅用于索引，不保存实际的数据；
3. 叶子节点之间通过指针连接，可以方便地进行顺序遍历。

B树和B+树常用于数据库索引结构，例如，MySQL数据库的InnoDB存储引擎就是使用B+树来组织索引数据。

# B树插入节点操作的简化伪代码

def BTreeInsert(T, k):
    t = T.root
    if len(t.keys) == 2*t.degree - 1:  # 树满
        u = TreeNode()
        T.root = u
        u.left = t
        BTreeSplitChild(u, 0)
        BTreeInsertNonFull(u, k)
    else:
        BTreeInsertNonFull(t, k)

def BTreeInsertNonFull(x, k):
    i = len(x.keys) - 1
    if isinstance(x, Leaf):
        while i >= 0 and x.keys[i] > k:
            x.keys[i+1] = x.keys[i]
            i -= 1
        x.keys[i+1] = k
    else:
        while i >= 0 and x.keys[i] > k:
            i -= 1
        i += 1
        if len(x.children[i].keys) == 2*x.degree - 1:
            BTreeSplitChild(x, i)
            if k > x.keys[i]:
                i += 1
        BTreeInsertNonFull(x.children[i], k)

在这个章节中，我们介绍了树型数据结构的基础概念、操作和应用。树结构以层次化的方式组织数据，特别适用于描述具有层次关系的信息，例如文件系统的目录结构、公司的组织结构图等。通过二叉树及其实现如AVL树和红黑树，我们能够维护数据的有序性和快速检索能力。而B树和B+树则适用于数据库系统中的磁盘存储，优化了大块数据的读取性能。这些数据结构在各种软件系统中广泛应用，是高级数据结构学习中的关键概念。

# 3. 图的数据结构

## 3.1 图的基本理论

### 3.1.1 图的定义和表示方法

图是一种数据结构，由顶点（也称节点或点）和连接顶点的边组成。图可以用来表示复杂的网络结构，比如社交网络、交通网络和互联网。图的表示方法主要有邻接矩阵和邻接表。

- 邻接矩阵是一种二维数组的表示方法，每个顶点都对应一个行和列，如果顶点u和顶点v之间有边，则矩阵的第u行第v列的