【数据结构与算法】

# 1. 数据结构与算法概述

在计算机科学和编程领域中，数据结构和算法是基础且核心的内容。本章将为读者提供这两个概念的全面概览，为后续章节中对具体数据结构和算法的深入分析打下坚实基础。

## 数据结构与算法的定义

数据结构是一门研究组织、存储、管理和检索数据的学科，它涉及数据的逻辑结构、物理存储结构以及这些数据结构上的操作算法。而算法则是解决特定问题的一系列定义良好的步骤。

## 数据结构与算法的重要性

它们对于开发高效和优化的软件至关重要。通过合理选择和实现数据结构，可以在信息检索、资源管理和数据操作方面提高程序的性能。掌握算法则可以优化解决问题的方法，降低资源消耗，提高计算效率。

## 学习数据结构与算法的目标

学习数据结构和算法不仅能够提高编程能力，还能培养良好的逻辑思维和抽象建模能力。这些技能对于准备技术面试、开发复杂的软件系统、以及为未来可能面对的新技术挑战做好准备都具有重要意义。

# 2. 核心数据结构分析

## 2.1 线性结构

线性结构是数据结构中最简单的一种类型，其元素之间存在一对一的关系，即除了第一个和最后一个元素之外，其它数据元素都是首尾相接的。在这一节中，我们将深入探讨数组和链表、栈和队列的基本概念、应用以及它们的操作原理和实现方法。

### 2.1.1 数组和链表的基本概念与应用

数组和链表是最常见的两种线性结构，它们在内存中的存储方式和操作方法各有千秋。数组是一种线性表数据结构，它用一段连续的内存空间来存储一组相同类型的数据。链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

数组适合用于读多写少的场景，因为它允许通过索引直接访问任何位置的元素，时间复杂度为O(1)。在随机访问频繁的场景中，数组可以提供良好的性能。然而，数组的大小在初始化后是固定的，且插入和删除操作需要移动大量元素，因此不太适合频繁增减元素的场景。

链表由于其节点之间的链接关系，允许在任何位置进行插入和删除操作，时间复杂度为O(1)，但其缺点是不能通过索引直接访问元素，需要从头节点开始遍历，所以时间复杂度为O(n)。链表非常灵活，适合用于写多读少的场景。

在实际应用中，数组常用于实现各种缓存策略，而链表则广泛用于实现数据的动态存储管理和复杂链表结构，如双向链表和循环链表。

// 示例：链表节点的定义
struct Node {
    int data;
    struct Node* next;
};

// 示例：数组的定义
#define MAX_SIZE 10
int array[MAX_SIZE];

以上代码分别展示了如何定义一个简单的链表节点和数组。在定义数组时，可以指定其最大容量，而链表的大小则是动态的，可根据需要随时添加新节点。

### 2.1.2 栈和队列的操作原理及实现

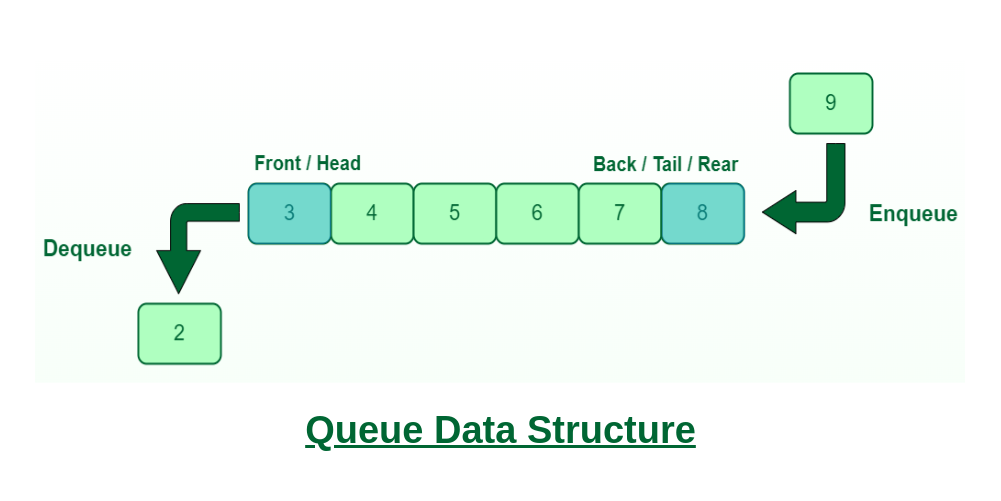
栈和队列是特殊的线性表，它们的元素插入和删除操作只限定在表的某一端，这使得它们具有“后进先出（LIFO）”和“先进先出（FIFO）”的特点。

栈（Stack）是一种后进先出的数据结构，只能在一端进行插入和删除操作。它的操作可以类比为一摞盘子，最后放上去的盘子必须是最先拿下来的。栈的操作通常包括压栈（push）、弹栈（pop）、查看栈顶元素（peek）等。

队列（Queue）是一种先进先出的数据结构，只允许在一端添加元素（入队），而在另一端删除元素（出队）。队列的操作可以类比为排队买票，先进来的顾客先接受服务。队列的主要操作包括入队（enqueue）、出队（dequeue）、查看队首元素（front）等。

// 示例：栈的简单实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX_SIZE 10

typedef struct Stack {
    int top;
    int data[MAX_SIZE];
} Stack;

bool push(Stack *s, int x) {
    if (s->top == MAX_SIZE - 1)
        return false;
    s->top++;
    s->data[s->top] = x;
    return true;
}

bool pop(Stack *s, int *x) {
    if (s->top == -1)
        return false;
    *x = s->data[s->top];
    s->top--;
    return true;
}

// 示例：队列的简单实现
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>

#define MAX_SIZE 10

typedef struct Queue {
    int front;
    int rear;
    int data[MAX_SIZE];
} Queue;

bool enqueue(Queue *q, int x) {
    if ((q->rear + 1) % MAX_SIZE == q->front)
        return false;
    q->data[q->rear] = x;
    q->rear = (q->rear + 1) % MAX_SIZE;
    return true;
}

bool dequeue(Queue *q, int *x) {
    if (q->front == q->rear)
        return false;
    *x = q->data[q->front];
    q->front = (q->front + 1) % MAX_SIZE;
    return true;
}

以上代码实现了栈和队列的基本操作，包括插入、删除和查看顶部或队首元素。在栈的操作中，使用了一个名为top的变量来追踪栈顶的位置。而在队列的操作中，使用了两个变量front和rear来追踪队首和队尾的位置。通过模运算实现循环队列，避免在队列为空时进行无效的访问。

通过本节的介绍，我们了解了线性结构的基本概念及其应用，并通过代码实例展示了如何实现数组、链表、栈和队列等常见线性结构。在下一节中，我们将继续探讨树形结构的遍历与操作，以及堆与优先队列的管理方法。

# 3. 经典排序与搜索算法

## 3.1 排序算法详述

### 3.1.1 冒泡、选择、插入排序的原理与实现

冒泡排序、选择排序、插入排序是最基础的三种排序算法，通常在算法学习的初期就被介绍。尽管它们在实际应用中效率不是最高，但在理解排序的基本概念和原理方面起着重要的作用。

#### 冒泡排序

冒泡排序是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小（或越大）的元素会经过交换慢慢“浮”到数列的顶端。

def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n-i-1):
            if arr[j] > arr[j+1]:
                arr[j], arr[j+1] = arr[j+1], arr[j]

example_array = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(example_array)
print(example_array)

在上述代码中，我们使用了一个双层循环，外层循环控制遍历次数，内层循环负责每轮的比较和交换。冒泡排序的时间复杂度为O(n^2)，并且它是一种稳定的排序算法。

#### 选择排序

选择排序是一种原址比较排序算法。它的工作原理是：首先在未排序序列中找到最小（或最大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（或最大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

def selection_sort(arr):
    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i+1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

example_array = [64, 25, 12, 22, 11]
selection_sort(example_array)
print(example_array)

选择排序同样具有O(n^2)的时间复杂度，但它是不稳定排序。它的优点是，只需要极少数的交换次数，且它不需要像冒泡排序一样在每轮结束后都做大量的元素交换。

#### 插入排序

插入排序的工作方式像玩扑克牌时整理牌的动作，即从头到尾进行遍历，将每个元素插入到已排序序列的适当位置。如果当前元素比前一个元素小，则交换它们，继续向前插入；如果当前元素比前一个元素大，则停止交换，因为已排序序列是有序的。

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i-1
        while j >=0 and key < arr[j]:
            arr[j+1] = arr[j]
            j -= 1
        arr[j+1] = key

example_array = [12, 11, 13, 5, 6]
insertion_sort(example_array)
print(example_array)

插入排序也是稳定的排序算法，其时间复杂度为O(n^2)，在最坏的情况下也是这样。尽管插入排序效率不高，但当输入数据接近已排序状态时，它将非常有效。

### 3.1.2 快速排序与归并排序的优化策略

快速排序和归并排序是两种更高效的排序算法，它们的平均时间复杂度为O(n log n)，在实际应用中比前述冒泡、选择、插入排序要常用。

#### 快速排序

快速排序的基本思想是选择一个元素作为“基准”（pivot），重新排列数组，使得所有比基准小的元素摆放在基准前面，所有比基准大的元素摆放在基准后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数组的中间位置。这个称为分区（partition）操作。递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

example_array = [3, 6, 8, 10, 1, 2, 1]
print(quick_sort(example_array))

快速排序在最好情况下时间复杂度为O(n log n)，但由于分区操作的性能对于快速排序的效率至关重要，因此其最坏情况下的时间复杂度为O(n^2)。实际应用中，可以通过随机选择基准或使用三数取中法等策略优化其性能。

#### 归并排序

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。归并排序是一种稳定的排序方法，和选择排序一样，归并排序的性能不受输入数据的影响，但表现比选择排序好的多，因为归并排序时间复杂度是O(n log n)。

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1