【数据科学必学】：利用正态分布提升模型性能的秘诀

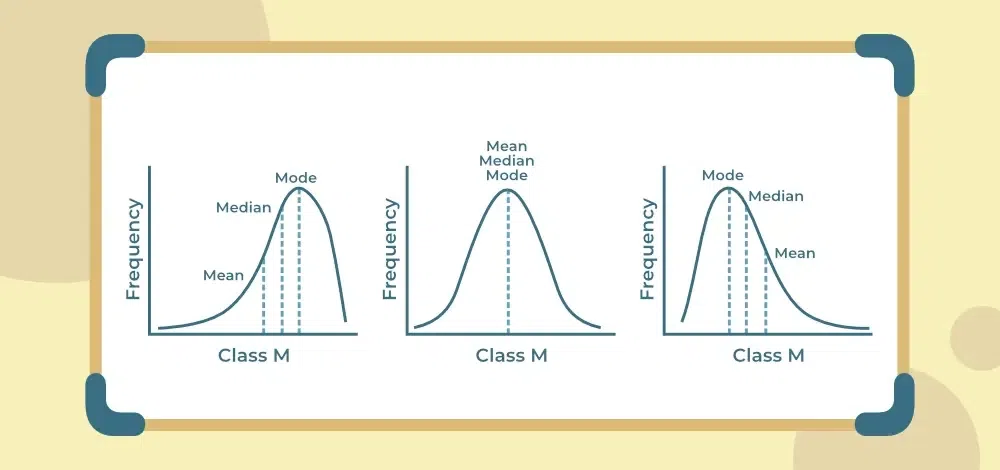
# 1. 数据科学中的正态分布概念

在数据科学的世界里，正态分布是基石之一，是许多分析和模型预设的天然语言。正态分布，又称高斯分布，它以数学家卡尔·弗里德里希·高斯的名字命名，因为它在自然界和社会现象中的普遍性而闻名。正态分布具有两个关键参数：均值（μ）和标准差（σ），这两个参数决定了分布的形状和数据的离散程度。通过理解正态分布，数据科学家们能够预测数据的行为，更有效地处理数据，以及在统计推断中做出更准确的决策。接下来的章节将深入探讨正态分布的数学原理，以及它在数据科学中的广泛应用。

# 2. 正态分布在数据科学中的理论基础

### 2.1 正态分布的数学定义

正态分布，也称为高斯分布，是自然界和社会科学领域中最为常见的一种概率分布。在数据科学中，理解其数学定义至关重要，因为这将有助于我们深入理解正态分布如何影响数据分析和模型构建。

#### 2.1.1 均值、方差和标准差的概念

正态分布的形状由两个主要参数决定：均值（mean）和方差（variance）。均值定义了分布的中心位置，它代表了数据集的平均值或期望值。方差衡量的是数据点相对于均值的离散程度，即数据分布的波动性。标准差是方差的平方根，它提供了用同一个单位来表示均值和数据点之间的距离的手段。

graph LR
    A[正态分布] -->|定义由| B(均值)
    A -->|定义由| C(方差)
    B -->|是| D[数据集的平均值或期望值]
    C -->|衡量| E[数据点与均值的离散程度]
    C -->|开方得到| F[标准差]
    F -->|表示| G[均值和数据点的距离]

均值、方差和标准差是描述数据集中趋势和离散程度的基本工具。例如，如果一个班级学生的考试成绩符合正态分布，则均值会告诉我们在平均意义上学生们的表现如何，而方差或标准差则会揭示这些成绩的波动范围。

#### 2.1.2 正态分布的概率密度函数

正态分布的概率密度函数（Probability Density Function，简称PDF）是一个关于均值和标准差的数学函数，用于描述数据点在某区间内出现的概率。其形式如下：

\[ f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

这里，\( x \) 是随机变量，\( \mu \) 是均值，\( \sigma^2 \) 是方差。函数图形呈现出一个钟形曲线，其对称轴位于均值 \( \mu \)，曲线在均值处达到最高点，随着距离均值的增加，概率密度迅速下降。

### 2.2 正态分布的性质和定理

#### 2.2.1 中心极限定理

中心极限定理（Central Limit Theorem, CLT）是概率论中非常重要的定理之一。它表明，无论总体分布如何，只要样本容量足够大，样本均值的分布将近似为正态分布。这一性质为数据科学提供了强大的统计推断工具。

中心极限定理的应用极其广泛，例如，在市场调查中，我们可能只对总体的一部分进行采样，根据CLT，即使原始总体分布不是正态的，样本均值的分布也会接近正态，这使得我们能够使用z分数（或t分数）进行置信区间的估计和假设检验。

#### 2.2.2 大数定律

大数定律（Law of Large Numbers, LLN）指出，当试验次数足够多时，样本均值会收敛到总体均值。简单来说，随着样本数量的增加，样本均值会越来越接近真实均值。

大数定律是抽样理论的基础。在实际应用中，我们常常基于有限的样本数据来推断总体情况，而大数定律保证了这种推断的可靠性和有效性。例如，通过大量顾客的购物行为数据来预测未来销售趋势。

### 2.3 正态分布与数据科学的关系

#### 2.3.1 数据标准化的重要性

在数据科学中，数据标准化是预处理过程的关键步骤之一。通过将数据标准化，即将数据转换为均值为0，标准差为1的分布，可以使得不同量纲和量级的数据变得可比，特别是在应用机器学习算法时，数据的尺度一致性非常关键。

标准化操作通常涉及从每个数据点中减去均值，然后除以标准差。数学上表示为：

\[ z = \frac{(x - \mu)}{\sigma} \]

其中，\( x \)是原始数据点，\( \mu \)是均值，\( \sigma \)是标准差，\( z \)是标准化后的数据点。

#### 2.3.2 正态分布与异常值检测

异常值指的是那些与数据集中的其他观测值显著不同的值。在许多情况下，异常值可能表示错误或重要的变异。利用正态分布可以检测异常值，因为正态分布具有特定的性质，即大部分数据（约99.7%）会落在均值的三个标准差范围内。

异常值检测可以应用于金融欺诈检测、网络入侵检测等多个领域。例如，一个正常的交易行为可能符合正态分布，如果出现了与均值偏离很大的交易，那么可能就是一笔欺诈交易。

正态分布在数据科学中不仅仅是一个简单的概率分布，它是许多理论和应用的基础。在后续章节中，我们将探讨正态分布如何在数据预处理、模型评估、深度学习优化等方面发挥作用，以及如何在实际中应用正态分布来提升模型性能。

# 3. 正态分布与模型性能提升的实践案例

## 3.1 数据预处理中的正态分布应用
### 3.1.1 数据清洗和标准化技术
在数据科学中，数据预处理是一个关键步骤，它对模型的性能有着直接的影响。数据清洗和标准化是数据预处理中最重要的技术之一，它们确保了数据的质量和一致性，为后续分析提供了坚实的基础。数据清洗主要是识别并处理缺失值、异常值和噪声数据。标准化技术则旨在将数据转换为一个通用的尺度，这样不同的特征或变量就可以直接比较和组合。

数据清洗过程中，识别异常值的一个有效方法就是假设数据遵循正态分布，并使用3σ原则（即三个标准差原则），识别超出这个范围的数据点作为异常值。处理这些数据点可以是删除、填补或替换。标准化技术如z-score标准化，通过从每个数据点中减去均值并除以标准差，将数据转换为均值为0，方差为1的标准正态分布。这在处理不同尺度和分布的特征时尤其重要。

### 3.1.2 特征缩放的方法和选择
在数据预处理阶段，特征缩放是提高模型性能的一种常用方法，尤其是在距离计算和梯度下降优化算法中。特征缩放的目的是将所有特征缩放到相同的尺度范围内，常用的特征缩放方法包括最小-最大标准化和z-score标准化。

最小-最大标准化将特征缩放到一个闭区间，通常是[0, 1]。公式如下：

X_scaled = (X - X_min) / (X_max - X_min)

其中`X`是原始特征，`X_min`和`X_max`是该特征的最小值和最大值，`X_scaled`是缩放后的特征值。

z-score标准化则使得特征的分布具有0的均值和1的标准差，即转换为标准正态分布。公式如下：

X_scaled = (X - μ) / σ

其中`μ`是特征的均值，`σ`是标准差，`X_scaled`是缩放后的特征值。

选择哪种方法取决于数据的性质和所用模型的需求。例如，神经网络通常需要z-score标准化，而一些基于距离的算法如K-最近邻（KNN）则更适宜使用最小-最大标准化。

## 3.2 模型评估中的正态分布
### 3.2.1 正态分布假设检验在模型评估中的作用
在模型评估中，假设检验是一个重要的步骤，特别是在回归分析和时间序列分析中。假设检验可以帮助我们了解模型参数的显著性以及预测结果是否可靠。正态分布假设检验，如t检验和F检验，在这里发挥着关键作用。

t检验用于评估单个均值或两个均值的差异是否显著，通常用于独立样本或配对样本的均值比较。其基本原理是：

t = (X̄ - μ) / (s / √n)

其中`X̄`是样本均值，`μ`是总体均值，`s`是样本标准差，`n`是样本大小。

F检验用于比较两个总体方差的差异是否显著。它基于以下公式：

F = s1^2 / s2^2

其中`s1^2`和`s2^2`是两个样本的方差。

### 3.2.2 应用正态分布进行A/B测试
A/B测试是一种比较两个版本的网页或应用以确定哪个版本性能更优的实验方法。在A/B测试中，转化率通常假设遵循正态分布，因此，正态分布理论可以用来确定版本之间的差异是否具有统计学意义。

为了进行这种测试，我们首先需要收集数据并计算两个版本的转化率均值和方差。然后，计算这两个样本均值的差异，并使用以下公式来计算z分数：

z = (X̄1 - X̄2) / √(σ1^2/n1 + σ2^2/n2)

其中`X̄1`和`X̄2`是两个版本的转化率均值，`σ1^2`和`σ2^2`是各自方差，`n1`和`n2`是样本大小。

根据z分数和显著性水平（如α=0.05），我们可以通过查找正态分布表来判断两个版本是否存在显著差异。如果z分数对应的P值小于α，那么我们拒绝原假设（即两个版本之间没有差异），认为两者存在统计学上的显著差异。

## 3.3 深度学习中的正态分布优化
### 3.3.1 权重初始化与正态分布
在深度学习中，权重初始化是训练神经网络时非常重要的一步。权重初始化不当可能导致模型训练失败，例如梯度消失或梯度爆炸。正态分布初始化是一种常见的方法，它根据均值和方差的设定，从正态分布中随机选取初始值赋予神经网络的权重。

权重初始化的方程通常如下：