霍夫变换直线检测：从理论到实践的完整指南

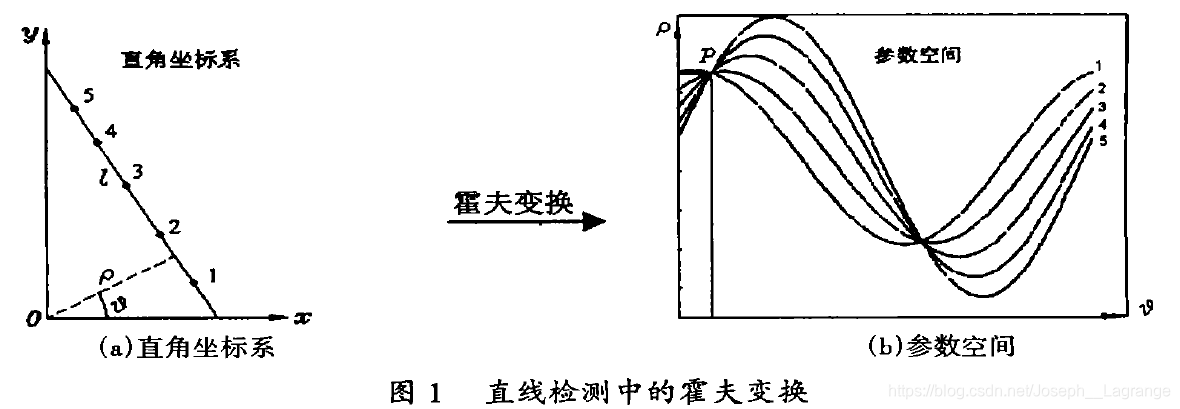
# 1. 霍夫变换的理论基础

霍夫变换是一种图像处理技术，用于检测特定形状，如直线、圆形和弧线。它基于一个简单的原理：一条直线在参数空间中表示为一个点。因此，通过对参数空间进行累加，我们可以找到图像中所有直线的交点，从而检测出直线。

霍夫变换的数学基础可以表示为：

ρ = x cos(θ) + y sin(θ)

其中：

* ρ 是直线到原点的距离
* θ 是直线与 x 轴之间的夹角
* x 和 y 是直线上的一个点

# 2. 霍夫变换直线检测的算法

### 2.1 标准霍夫变换

**原理：**

标准霍夫变换是一种基于参数空间的直线检测算法。它将图像中的每个边缘点映射到参数空间中的正弦曲线，其中正弦曲线的参数对应于直线的斜率和截距。

**算法步骤：**

1. **边缘检测：**使用边缘检测算法（如 Canny 算子）检测图像中的边缘点。
2. **参数空间累加：**对于每个边缘点，计算其正弦曲线在参数空间中的所有可能值。在参数空间中累加这些正弦曲线的交点。
3. **直线提取：**在参数空间中找到局部最大值，这些局部最大值对应于图像中检测到的直线。

**代码示例：**

import numpy as np
import cv2

def standard_hough_transform(image):
    # 边缘检测
    edges = cv2.Canny(image, 100, 200)

    # 参数空间累加
    hough_space = np.zeros((360, image.shape[0]))
    for y in range(image.shape[0]):
        for x in range(image.shape[1]):
            if edges[y, x] > 0:
                for theta in range(360):
                    r = x * np.cos(theta * np.pi / 180) + y * np.sin(theta * np.pi / 180)
                    hough_space[theta, int(r)] += 1

    # 直线提取
    lines = []
    for theta in range(360):
        for r in range(image.shape[0]):
            if hough_space[theta, r] > 100:
                lines.append((theta, r))

    return lines

**参数说明：**

* `image`: 输入图像
* `lines`: 检测到的直线列表，每个元素为一个元组，包含直线的斜率和截距

### 2.2 概率霍夫变换

**原理：**

概率霍夫变换是一种改进的霍夫变换算法，它通过随机采样来提高检测速度。它只计算边缘点正弦曲线的随机子集，并使用这些子集来累加参数空间。

**算法步骤：**

1. **边缘检测：**使用边缘检测算法检测图像中的边缘点。
2. **随机采样：**从边缘点中随机选择一个子集。
3. **参数空间累加：**对于每个采样的边缘点，计算其正弦曲线在参数空间中的所有可能值。在参数空间中累加这些正弦曲线的交点。
4. **直线提取：**在参数空间中找到局部最大值，这些局部最大值对应于图像中检测到的直线。

**代码示例：**

import numpy as np
import cv2

def probabilistic_hough_transform(image, num_samples=100):
    # 边缘检测
    edges = cv2.Canny(image, 100, 200)

    # 随机采样
    sampled_edges = np.random.choice(np.where(edges > 0), num_samples, replace=False)

    # 参数空间累加
    hough_space = np.zeros((360, image.shape[0]))
    for y, x in sampled_edges:
        for theta in range(360):
            r = x * np.cos(theta * np.pi / 180) + y * np.sin(theta * np.