机器学习性能评估：时间复杂度在模型训练与预测中的重要性

# 1. 机器学习性能评估概述

## 1.1 机器学习的性能评估重要性
机器学习的性能评估是验证模型效果的关键步骤。它不仅帮助我们了解模型在未知数据上的表现，而且对于模型的优化和改进也至关重要。准确的评估可以确保模型的泛化能力，避免过拟合或欠拟合的问题。

## 1.2 性能评估指标的选择
选择正确的性能评估指标对于不同类型的机器学习任务至关重要。例如，在分类任务中常用的指标有准确率、精确率、召回率和F1分数；而回归问题可能使用均方误差或决定系数。根据应用需求选择适当的评估指标是至关重要的。

## 1.3 本章小结
本章从宏观角度介绍了机器学习性能评估的必要性和常用指标。在后续章节中，我们将深入探讨时间复杂度以及它如何影响机器学习模型的性能评估，为我们提供更全面的理解和解决方案。

# 2. 时间复杂度基础理论

### 2.1 时间复杂度的定义与计算

#### 2.1.1 大O符号表示法

在计算机科学中，大O符号表示法是一种表达算法性能上界和下界的方式。它被用来描述算法运行时间的上限，忽略常数因子和低阶项。对于一个给定的函数g(n)，大O符号表示的是一个集合，这个集合包含了所有增长不超过g(n)乘以某个正常数c的函数f(n)。具体来说，如果一个算法的执行时间以n（输入大小）的函数来表示，那么大O符号表示的上界就是这个函数最坏情况下增长的速率。

flowchart TD
    A[算法性能] -->|忽略常数和低阶项| B[大O符号表示]
    B --> C[上界]
    B --> D[下界]

以一个简单的线性搜索算法为例，其时间复杂度可以用大O表示为O(n)，表示其执行时间与输入数据量n成线性关系。

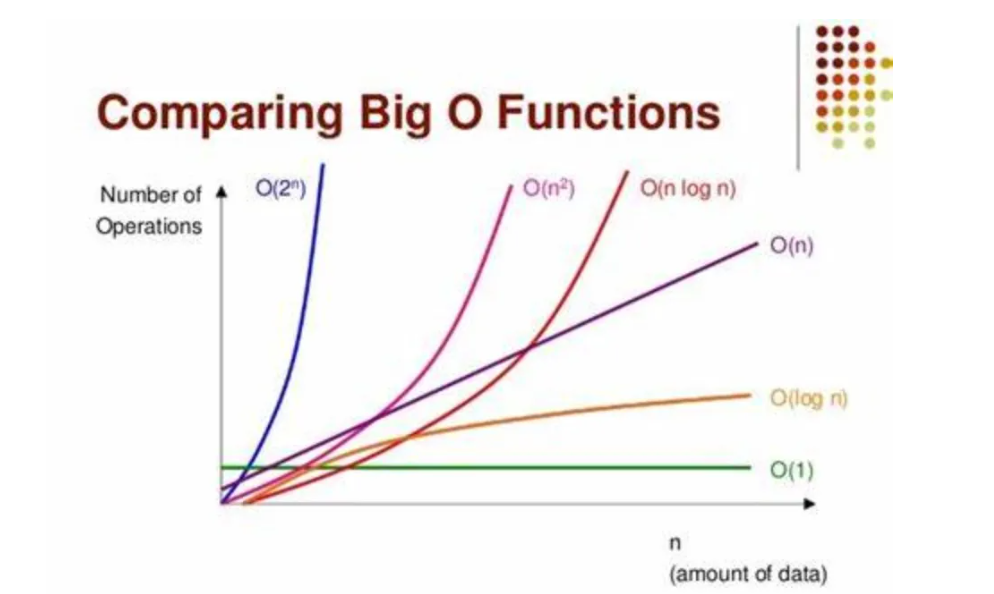
#### 2.1.2 时间复杂度的常见类别

时间复杂度有多种类别，最常见的是以下几种：

- **常数时间复杂度**：O(1)，表示执行时间与输入数据量无关。
- **对数时间复杂度**：O(log n)，通常出现在二分查找算法中。
- **线性时间复杂度**：O(n)，如上所述的线性搜索。
- **线性对数时间复杂度**：O(n log n)，常见于高效的排序算法如快速排序、归并排序。
- **多项式时间复杂度**：O(n^2)，O(n^3)等，常见于简单的排序和搜索算法。
- **指数时间复杂度**：O(2^n)，常见于解决NP完全问题的算法。
- **阶乘时间复杂度**：O(n!)，这类算法的性能随着数据量的增加而急剧下降。

每类时间复杂度反映了算法处理数据量增长时性能的变化趋势，是分析和比较算法效率的关键指标。

### 2.2 算法效率分析

#### 2.2.1 最坏情况、平均情况与最好情况分析

算法的效率可以通过考虑不同情况下的性能来进行分析，其中最重要的三种情况是：

- **最坏情况分析**（Worst-case analysis）：在最坏情况下算法需要执行的步骤数。这是在安全性要求高的应用中最为关键的性能度量，例如金融交易系统。
- **平均情况分析**（Average-case analysis）：在所有可能的输入数据中，算法执行的平均步骤数。这通常更接近于算法在实际中的性能表现。
- **最好情况分析**（Best-case analysis）：在最佳可能情况下算法需要执行的步骤数。虽然在实际情况中很少遇到，但有时可以为算法性能提供下限保证。

在分析算法时，我们经常关注最坏情况，因为它为我们提供了一个性能的保证。但在一些应用中，平均情况分析可能更具有实际意义。

#### 2.2.2 算法的递归与迭代效率比较

在算法设计中，递归和迭代是实现算法的两种常见方式。它们各有优劣，并且往往对应不同的时间复杂度。

- **递归**（Recursive）：递归函数调用自身来解决问题的一部分，然后将这些部分的解组合起来。递归的效率往往和递归深度以及每次递归调用的复杂度有关，且在某些情况下可能会有重复计算的问题。
- **迭代**（Iterative）：通过循环结构对问题进行迭代求解，通常效率较高，因为没有函数调用的开销，并且避免了重复计算。

比较两种方法的效率时，我们通常会考虑以下几个因素：时间复杂度、空间复杂度和程序的可读性及可维护性。在很多情况下，递归算法可以更容易编写，但迭代算法可能具有更低的时间复杂度，尤其是在可以避免递归中产生的额外空间开销时。

### 2.3 时间复杂度与空间复杂度的关系

#### 2.3.1 时间-空间权衡

时间复杂度与空间复杂度之间存在一种权衡关系。有时，我们可以通过牺牲一些计算时间来减少对存储空间的需求，或者反过来。这种权衡在算法设计中非常重要，尤其是在资源受限的情况下。例如，一些排序算法可以在较短的时间内完成排序，但需要额外的空间（如归并排序），而其他排序算法（如冒泡排序）可能在不使用额外空间的情况下运行，但时间效率较低。

在优化算法时，开发者需要根据实际应用场景的需求来决定是优先考虑时间效率还是空间效率，或者在两者之间寻找一个平衡点。

#### 2.3.2 复杂度在实际应用中的权衡实例

在实际应用中，时间复杂度和空间复杂度的权衡取决于具体的应用需求。例如，在内存非常有限的嵌入式系统中，开发者可能会选择使用时间复杂度较高的算法以节省内存空间。而在处理大规模数据的服务器上，尽管需要消耗更多的内存，使用时间复杂度更低的算法可以大大提高处理速度，从而提高整体系统的性能。

具体而言，我们可以考虑以下两种常见情景：

- **图算法**：在处理大型网络数据时，图算法（如最短路径算法）可能会面临时间复杂度和空间复杂度之间的权衡。例如，Dijkstra算法通常需要额外的空间来存储最短路径树，但执行时间相对较短。而Bellman-Ford算法虽然空间要求不高，但其时间复杂度较高，不适合处理大规模网络数据。
- **文本处理**：在处理大量文本数据时，如在搜索引擎中索引网页，空间复杂度可能更为关键。一些高效的压缩算法可以在不显著牺牲时间复杂度的情况下，大幅减少存储空间的需求，从而在有限的存储资源下保持较快的处理速度。

这种权衡在不同的应用场景中可能会有不同的考虑和平衡点，但基本原则是相同的：开发者需要根据实际情况和资源限制来选择最合适的算法。

# 3. 机器学习模型训练中的时间复杂度

在机器学习领域，模型训练阶段是理解和评估时间复杂度的关键环节。时间复杂度不仅影响模型的训练速度，还会对模型的最终性能产生重要影响。本章将深入探讨训练过程中时间复杂度的分析方法，优化策略，以及时间复杂度在实际模型选择中的作用。

## 3.1 训练过程的时间复杂度分析

### 3.1.1 模型训练阶段的关键步骤

在机器学习模型训练的整个过程中，存在着多个关键步骤，包括数据加载、预处理、模型参数更新、评估和验证等。每个步骤的时间消耗在不同算法中表现出不同的复杂度特征。

首先，数据加载通常涉及I/O操作，其时间复杂度依赖于存储介质的读取速度和数据量大小。数据预处理包括标准化、归一化、缺失值处理等，其时间复杂度会随着数据集的大小呈线性增长，具体操作如归一化通常时间复杂度为O(n)，其中n是样本数量。

接下来，模型参数更新环节，对于基于梯度的优化算法，如随机梯度下降（SGD），每次迭代的计算量主要由模型参数数量决定，时间复杂度为O(w)，w表示模型参数总数。而像神经网络这样的复杂模型，其时间复杂度可高达O(w^2)或更高，特别是在使用全连接层时。

模型评估和验证涉及将训练好的模型应用于验证集并计算性能指标，其时间复杂度与模型类型和验证集大小相关。对于分类问题，通常为O(n)，其中n是验证集样本数量。

### 3.1.2 不同机器学习算法的时间复杂度比较

机器学习算法由于其不同的数学原理和计算流程，具有不同的时间复杂度。例如，决策树在构建时需要对每个特征进行分割点的评估，其时间复杂度一