存储与效率的权衡：空间复杂度与时间复杂度的关联解析

# 1. 引言：理解存储与效率的重要性

在当今信息爆炸的时代，数据存储和处理效率是衡量信息技术系统性能的关键指标。无论是大数据分析、云计算服务还是边缘计算，存储空间的高效利用以及算法执行的快速响应都是至关重要的。存储效率直接影响到成本控制，而执行效率则关乎用户体验和市场竞争力。本章将简要介绍存储和效率的重要性，为后续章节的深入探讨打下基础。

## 1.1 现代信息技术的需求

随着互联网和物联网技术的飞速发展，企业和个人用户产生的数据量呈指数级增长。这些数据需要被存储、处理和分析，以实现信息的高效流通和知识的提炼。因此，高效的数据存储解决方案和算法优化成为了技术进步的核心。

## 1.2 效率的衡量标准

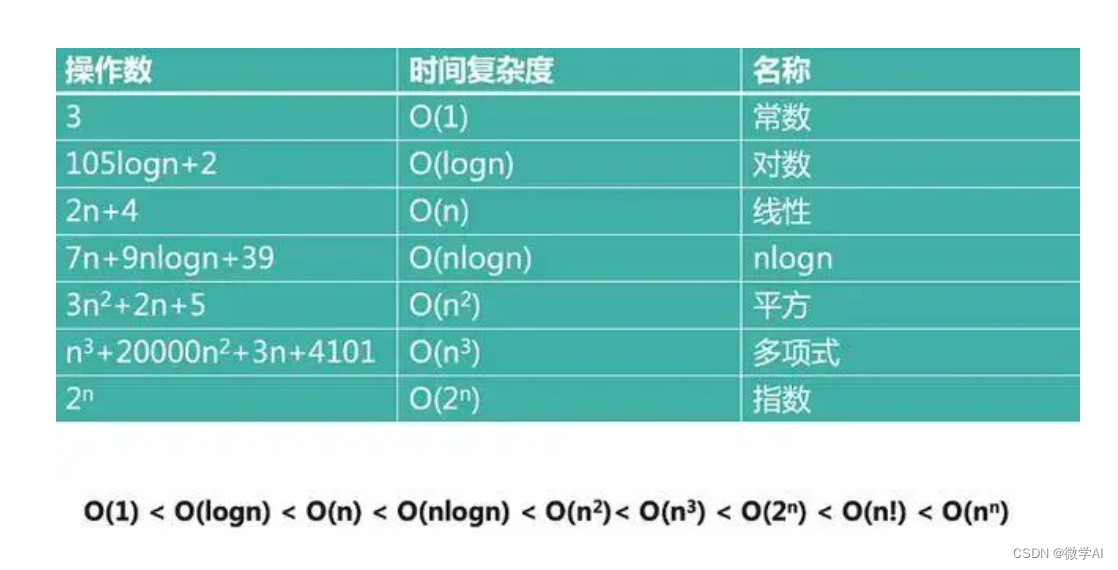
在信息技术领域，效率通常通过时间复杂度和空间复杂度来衡量。时间复杂度关注算法执行所需的时间，与硬件性能和软件算法都有密切关系。空间复杂度则关注算法执行过程中占用的内存或存储空间。理解并优化这两个方面，对于提升系统的整体性能至关重要。

在本章中，我们仅仅触及了存储与效率重要性的皮毛，接下来章节将通过具体实例和深入分析，带领读者深入探索空间与时间复杂度的奥秘。

# 2. 空间复杂度基础

## 2.1 空间复杂度的定义和重要性

### 2.1.1 空间复杂度的含义

在计算机科学中，空间复杂度是指完成算法所需的存储空间。它通常以算法所处理的数据量为基础，与数据规模 n 相关。空间复杂度是一个函数，它表示随着输入数据规模的增加，所需的额外空间量是如何变化的。

空间复杂度的核心在于区分固定空间和额外空间：
- 固定空间是指程序在执行之前就已经分配好的，无论输入数据大小如何都不发生变化的空间。
- 额外空间是指在执行算法的过程中，除了输入数据所需的空间外，算法额外申请的空间。

### 2.1.2 空间复杂度对效率的影响

空间复杂度是衡量算法效率的重要指标之一，尤其在资源受限的环境下更是如此。例如，在嵌入式系统或移动设备中，可用内存是有限的，过度的内存使用可能导致程序崩溃或降低性能。

在设计算法时，尽可能优化空间复杂度以适应不同的运行环境，对于提高算法的通用性和可靠性至关重要。在某些情况下，通过算法优化，可以在不显著增加时间复杂度的前提下，大大减少空间的使用。

## 2.2 空间复杂度的评估方法

### 2.2.1 常数空间与线性空间

空间复杂度的评估从最基本的类别开始：常数空间和线性空间。

- 常数空间（O(1)）：表示算法的空间需求不随输入数据的大小变化而变化。例如，使用固定数量的变量或常量大小的数组。
- 线性空间（O(n)）：空间需求随输入数据的大小成线性比例增长。例如，使用长度为 n 的数组。

graph TD
    A[算法] -->|空间需求| B[常数空间]
    A -->|空间需求| C[线性空间]

### 2.2.2 对数、二次和三维空间复杂度

随着问题规模的增加，空间复杂度可以呈对数、二次或三次方增长，分别表示为 O(log n)、O(n^2) 和 O(n^3)。

- 对数空间：常见于需要访问数据的索引可以对数级别缩小的情况，如二分查找算法。
- 二次空间：通常出现在需要使用二维数组或嵌套循环处理数据的算法中。
- 三维空间：在三维数据处理，或三层嵌套循环中使用。

### 2.2.3 高级数据结构的空间复杂度分析

高级数据结构如哈希表、平衡树、图等，在空间复杂度上表现出特定的特征，需单独分析：

- 哈希表通常具有 O(n) 的空间复杂度，但考虑到哈希冲突和扩容，实际的空间可能稍多。
- 平衡树（如红黑树、AVL树）的空间复杂度为 O(n)。
- 图结构的空间复杂度取决于表示方法，邻接矩阵可能为 O(n^2)，而邻接表为 O(n + m)，其中 n 是顶点数，m 是边数。

## 2.3 实际案例分析：空间优化策略

### 2.3.1 缓存策略

缓存是一种常见的减少空间需求的技术。通过将频繁访问的数据暂存于快速访问的内存中，可以有效减少对原始数据存储（如硬盘）的依赖。

# 示例：简单的缓存策略实现
def get_data(key):
    # 检查缓存中是否存在key
    if key in cache:
        return cache[key]  # 直接返回缓存中的数据
    else:
        data = fetch_data_from_disk(key)  # 从硬盘获取数据
        cache[key] = data  # 存入缓存
        return data

cache = {}  # 初始化缓存

通过上述方法，可以有效减少对硬盘的读取次数，提升整体效率。在实践中，实现缓存策略需要考虑缓存容量、替换策略和缓存一致性等问题。

### 2.3.2 数据压缩技术

数据压缩是另一种节省空间的方法，它通过算法减少数据的冗余部分，达到减小数据体积的目的。

在软件开发中，常见的数据压缩方法包括：
- Gzip压缩：广泛应用于文本文件的压缩，尤其在网络传输中效率高。
- Run-length 编码：适用于有大量重复数据的场景。
- Huffman编码：根据数据出现频率的不同，用不同长度的编码表示数据。

# 示例：使用Gzip压缩和解压文本数据
import gzip
import shutil

# 压缩数据
with open('data.txt', 'rb') as f_in:
    with gzip.open('data.txt.gz', 'wb') as f_out:
        shutil.copyfileobj(f_in, f_out)

# 解压数据
with gzip.open('data.txt.gz', 'rb') as f_in:
    with open('data.txt', 'wb') as f_out:
        shutil.copyfileobj(f_in, f_out)

使用数据压缩技术可以有效减少存储空间占用，尤其在网络传输中可以大幅减少数据传输量，提升效率。

# 3. 时间复杂度基础

## 3.1 时间复杂度的定义和重要性

### 3.1.1 时间复杂度的含义

时间复杂度是衡量算法运行时间效率的标准，通常表示为输入大小n的函数。时间复杂度越高，算法处理大数据量时的效率越低。它能帮助开发者了解算法的性能，并预估在不同规模的数据集上运行算法所需的时间。

### 3.1.2 时间复杂度对性能的影响

一个算法的时间复杂度决定了其在实际应用中的可行性。例如，具有较高时间复杂度的算法在处理大量数据时可能会非常缓慢，导致应用程序响应变慢甚至无法完成任务。因此，理解并优化时间复杂度是提升软件性能的关键。

## 3.2 时间复杂度的计算和分类

### 3.2.1 常数时间、线性时间与多项式时间

- **常数时间 (O(1))**：算法的执行时间不依赖于输入数据的大小，如访问数组中的元素。
- **线性时间 (O(n))**：算法的执行时间与输入数据的大小成正比，如遍历数组。
- **多项式时间 (O(n^k))**：算法的执行时间与输入数据的大小的多项式成正比，其中k为常数。例如，对数组进行双重循环即为O(n^2)。

### 3.2.2 对数时间与指数时间复杂度

- **对数时间 (O(log n))**：算法的执行时间与输入数据大小的对数成正比，常见于分而治之的算法。
- **指数时间