回溯算法优化实战：剪枝技术与时间复杂度的重要性

# 1. 回溯算法基础

## 1.1 回溯算法的定义
回溯算法是一类问题求解的方法，通过探索所有可能的候选解来找出所有解。如果候选解被确认不是一个解，则回溯并且尝试下一个可能的候选解。

## 1.2 算法工作原理
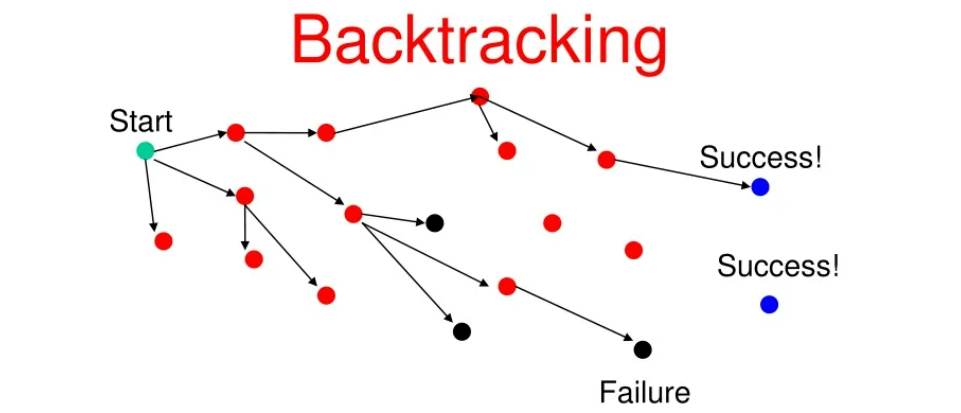
基本思想是递归地尝试每一个可能的路径，一旦发现当前路径不可能产生有效的解决方案，就会回退到上一步进行重新选择。这个过程中可能会放弃大量当前路径上的节点，从而显著降低问题的搜索空间。

## 1.3 算法的关键要素
关键在于“回溯”二字，即当算法到达某一节点发现当前选择不可能产生问题的解时，撤销上一步或几步的计算，回退到上一个节点，并在其他方向进行试探。

通过这个过程，回溯算法保证了找到所有可能的解，并且尽可能高效地减少不必要的搜索，其在解决诸如N皇后、图的着色问题以及许多组合优化问题中都发挥着重要作用。

# 回溯算法的一般结构伪代码
def backtrack(路径, 选择列表):
    if 满足结束条件:
        存储解
        return
    for 选择 in 选择列表:
        做出选择
        backtrack(路径, 选择列表)
        撤销选择

这个伪代码显示了回溯算法的基础框架，关键在于在满足结束条件时存储解，并且在递归调用后撤销所做的选择，以此来探索其他的可能路径。在实际应用中，算法的效率高度依赖于选择列表和结束条件的设计。

# 2. 剪枝技术的原理与应用

## 2.1 剪枝技术概述

### 2.1.1 剪枝技术的定义
剪枝技术是一种常见的优化方法，通过减少搜索树的节点数量来降低问题求解的复杂度。在回溯算法中，剪枝操作通常发生在生成新节点时。如果当前节点不可能产生有效解，或者通过某种方式判断出该节点的所有子节点都不会对最终解有贡献，则可以“剪掉”这个节点，不再进一步探索其子节点。

剪枝技术的核心思想是减少不必要的计算，提高算法效率。在实际应用中，剪枝技术可以在不影响解的正确性和完整性的情况下，显著减少搜索空间，从而加快算法的求解速度。

### 2.1.2 剪枝技术的作用
剪枝技术的作用在于它能够有效地提升算法的性能，主要表现在以下几个方面：
1. **提高效率**：通过剪去无效或不可能的分支，减少需要处理的节点数量，从而加快算法的求解速度。
2. **降低内存消耗**：较少的节点意味着较低的内存使用，尤其是在解决大规模问题时更为明显。
3. **优化算法时间复杂度**：剪枝能够减少算法的时间复杂度，尤其是对于指数型增长的搜索问题，其效果尤为显著。
4. **提升可扩展性**：剪枝技术使得算法能够处理更大规模的问题实例，提高了算法的适用范围。

## 2.2 常见剪枝策略

### 2.2.1 限界剪枝
限界剪枝是一种基于问题约束的剪枝方法。在搜索过程中，通过设定一个界限值来决定是否继续探索某个节点。如果一个节点的当前值已经超出了可能达到最优解的界限，那么该节点及其所有子节点都可以被剪去。

限界剪枝的关键在于正确设置界限值，这个界限值通常根据问题的特性及已有的信息动态计算得出。例如，在旅行商问题（TSP）中，如果当前路径的长度已经超过了已知的最短路径长度，那么这个路径分支可以被剪去。

def bound(node, best):
    # 假设bound函数根据当前节点的状态和已知的最优解来计算界限值
    # 如果当前节点的潜在最优解已经大于已知的最优解，则返回负无穷表示剪枝
    if potential_best(node) > best:
        return float('-inf')
    # 否则返回界限值
    return potential_best(node)

def search(node, best):
    # 伪代码，展示如何使用界限值进行剪枝
    if bound(node, best) == float('-inf'):
        return
    # 正常的回溯算法搜索过程
    ...

### 2.2.2 启发式剪枝
启发式剪枝依赖于问题特定的经验法则，通过评估节点的优先级来决定是否继续搜索。这种方法不需要严格证明，而是根据经验判断某个节点是否有可能导致更好的解。

例如，在图着色问题中，如果某个节点的颜色选择空间已经非常小，那么可以优先搜索这个节点，反之则可能将其剪去。

def heuristic_pruning(node):
    # 使用启发式评估当前节点的优先级
    priority = evaluate_priority(node)
    # 如果优先级低于某个阈值，则剪枝
    if priority < THRESHOLD:
        return True
    return False

def search(node):
    # 伪代码，展示如何使用启发式剪枝
    if heuristic_pruning(node):
        return
    # 正常的回溯算法搜索过程
    ...

### 2.2.3 记忆化剪枝
记忆化剪枝是一种存储已经计算过的节点结果，避免重复计算的技术。通常使用一个哈希表来记录节点的状态和对应的最优解或剪枝信息。当遇到状态相同的节点时，直接从记忆中获取信息，无需重复计算。

记忆化剪枝特别适合于具有大量重复子问题的优化问题，如动态规划问题。在回溯算法中，记忆化剪枝可以减少重复的搜索工作，从而加速算法运行。

def memoization(node, solutions):
    # 将当前节点的状态作为键，搜索结果作为值
    key = generate_key(node)
    if key in solutions:
        return solutions[key]
    # 正常的回溯算法搜索过程
    result = ...
    solutions[key] = result
    return result

def search(node):
    solutions = {}
    # 伪代码，展示如何使用记忆化剪枝
    return memoization(node, solutions)

## 2.3 剪枝技术的实践案例

### 2.3.1 N皇后问题的剪枝实现
N皇后问题是一个经典的回溯问题，要求在一个N×N的棋盘上放置N个皇后，使得它们互不攻击（即任意两个皇后都不在同一行、同一列及同一斜线上）。

在解决N皇后问题时，可以通过剪枝技术显著提高求解效率。例如，在放置第i个皇后时，可以检查当前列和对角线是否已经有皇后存在，如果存在，则剪去这个分支。

### 2.3.2 算法竞赛中的剪枝应用
在算法竞赛中，剪枝技术的应用可以极大地提高算法的性能。许多题目可以转化为图问题、搜索问题或者组合优化问题，通过剪枝可以快速找到问题的解决方案或者验证解的正确性。

例如，在解决组合优化问题时，可以利用问题的对称性或者特殊性质，来剪去那些明显不可能包含最优解的分支。在某些情况下，甚至可以根据题目的限制条件精确地计算出剪枝的界限值，实现高效的搜索过程。

def prune_symmetry(node):
    # 利用对称性进行剪枝
    if symmetry_condition(node):
        return True
    return False

def search(node):
    # 伪代码，展示如何在算法竞赛中使用剪枝
    if prune_symmetry(node):
        return
    # 正常的回溯算法搜索过程
    ...

通过上述的介绍，我们了解了剪枝技术的定义