图算法深度剖析：从DFS到Dijkstra的时间复杂度优化策略

目录
1. 图算法基础与深度优先搜索（DFS）

1.1 图算法简介
1.2 深度优先搜索（DFS）介绍

示例代码（DFS遍历无向图）

1.3 深度优先搜索的应用场景

2. Dijkstra算法原理与应用

2.1 Dijkstra算法概述

2.1.1 算法原理
2.1.2 算法特点
2.1.3 算法伪代码

2.2 Dijkstra算法的时间复杂度

2.2.1 时间复杂度分析
2.2.2 空间复杂度分析
2.2.3 算法优化方向

2.3 Dijkstra算法的应用实例

2.3.1 路由选择
2.3.2 地图导航
2.3.3 实际代码实现

解锁专栏，查看完整目录
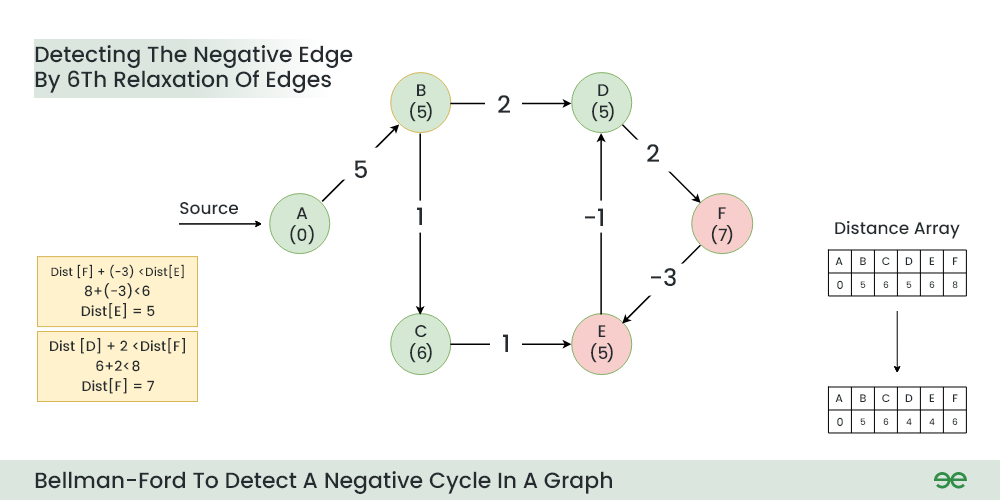
1. 图算法基础与深度优先搜索（DFS）
1.1 图算法简介
图算法是一类处理图形数据结构问题的算法，广泛应用于计算机科学、社交网络、生物信息学等领域。图由节点（也称为顶点）和连接它们的边组成，能够描绘元素之间的复杂关系。图算法可以帮助我们解决路径查找、网络设计、资源分配等多种问题。
1.2 深度优先搜索（DFS）介绍
深度优先搜索是一种用于遍历或搜索树或图的算法。在图中执行DFS时，算法从一个节点开始，沿着一条路径深入探索，直到无法继续前进，然后回溯并尝试其他路径。这种方法在解决迷宫问题、拓扑排序、寻找连通分量等任务中非常有效。
示例代码（DFS遍历无向图）
# Python示例代码，表示DFS遍历无向图# 假设我们有一个图的邻接表表示graph = { 'A': ['B', 'C'], 'B': ['A', 'D', 'E'], 'C': ['A', 'F'], 'D': ['B'], 'E': ['B', 'F'], 'F': ['C', 'E']}# 初始化访问标记visited = set()def dfs(visited, graph, node): # dfs函数定义 if node not in visited: print(node) visited.add(node) for neighbour in graph[node]: dfs(visited, graph, neighbour)# 从节点'A'开始深度优先遍历dfs(visited, graph, 'A')登录后复制
1.3 深度优先搜索的应用场景
DFS在许多领域都有广泛应用。例如，在有向图中使用DFS可以判断是否存在回路。在游戏开发中，DFS被用来追踪最优解路径，如在棋盘游戏中找到从起点到终点的最佳走法。在网络安全领域，DFS可以用于检测和分析病毒的传播路径。
通过本章的学习，我们将打下图算法和DFS的基础，为后续章节中复杂图算法的时间复杂度优化和实际应用案例分析奠定基础。
2. Dijkstra算法原理与应用
2.1 Dijkstra算法概述
Dijkstra算法是最著名的最短路径算法之一，由荷兰计算机科学家Edsger W. Dijkstra在1956年提出，并于1959年发表。该算法用于在加权图中找到两个节点之间的最短路径，尤其是当图中边的权重非负时，Dijkstra算法可以保证找到最优解。
2.1.1 算法原理
Dijkstra算法采用贪心策略，逐步构建起从起始点到其他所有可达节点的最短路径。算法从源点开始，初始化源点到自身的距离为0，到其他所有点的距离为无穷大。然后重复以下步骤，直到所有节点的最短路径被确定：

从未处理的节点中选择一个距离源点最近的节点u。
更新节点u所有相邻节点v的距离，如果通过u到v的距离比已知的最短路径短，则更新最短路径值。
标记节点u为已处理。

2.1.2 算法特点
Dijkstra算法有以下显著特点：

正权边：算法要求图中的所有边的权重必须是非负的。
单源最短路径：算法计算的是从单个源点出发到图中所有其他节点的最短路径。
贪心思想：在每一步中选择当前看来最优的选择，即距离最短的节点。

2.1.3 算法伪代码
Dijkstra(Graph, source): create vertex set Q for each vertex v in Graph: dist[v] ← INFINITY prev[v] ← UNDEFINED add v to Q dist[source] ← 0 while Q is not empty: u ← vertex in Q with min dist[u] remove u from Q for each neighbor v of u: // only v that are still in Q alt ← dist[u] + length(u, v) if alt < dist[v]: dist[v] ← alt prev[v] ← u return dist[], prev[]登录后复制
2.2 Dijkstra算法的时间复杂度
2.2.1 时间复杂度分析
Dijkstra算法的时间复杂度取决于所采用的数据结构。最朴素的实现方式是使用邻接矩阵，时间复杂度为O(V^2)，其中V是顶点的数量。当使用优先队列（例如二叉堆）时，可以将时间复杂度降低到O((V+E)logV)，其中E是边的数量。这是因为每次从优先队列中取出最小距离节点的操作复杂度为O(logV)，而更新相邻节点距离的操作复杂度为O(1)。
2.2.2 空间复杂度分析
Dijkstra算法的空间复杂度主要由存储距离信息和节点前驱信息的数组决定，因此空间复杂度为O(V)。
2.2.3 算法优化方向
由于Dijkstra算法的时间复杂度与边的数量E成正比，优化方向主要集中在减少对边的处理次数和优化数据结构上。例如：

使用斐波那契堆可以将时间复杂度进一步降低到O(VlogV + E)。
对于稠密图，可以使用邻接矩阵表示图，快速访问任意两点之间的距离。
对于稀疏图，则可以使用邻接表，并配合优先队列优化算法性能。

2.3 Dijkstra算法的应用实例
2.3.1 路由选择
Dijkstra算法在很多与网络相关的应用中都有应用，如网络路由选择。在该应用场景下，路由器会利用Dijkstra算法计算到达网络中其他路由器的最短路径。
2.3.2 地图导航
在地图应用中，Dijkstra算法被用来计算从一个地点到另一个地点的最短路径。无论是步行、驾车还是公共交通，该算法都可用于最优路径的计算。
2.3.3 实际代码实现
以下是Dijkstra算法的一个简单实现，使用Python语言和标准库中的堆结构进行优化。
import heapqdef dijkstra(graph, start): distances = {vertex: float('infinity') for vertex in graph} distances[start] = 0 priority_queue = [(0, start)] while priority_queue: current_distance, current_vertex = heapq.heappop(priority_queue) if current_distance > distances[current_vertex]: continue for neighbor, weight in graph[current_vertex].items(): distance = current_distance + weight if distance < distances[neighbor]: distances[neighbor] = distance heapq.heappush(priority_queue, (distance, neighbor)) return distances登录后复制