【软件应用】：用Excel释放线性优化的力量，助你高效决策


# 摘要
本文深入探讨了线性优化基础及其与Excel软件的契合度，阐述了Excel在构建和解决线性优化模型中的广泛应用。从理论基础到具体应用，本文详细讲解了线性优化模型的构建过程，包括设计输入数据表格、建立目标函数和约束条件，并使用Excel求解器进行求解。同时，本文还分析了模型结果，包括如何解读求解器输出以及进行敏感性分析以评估模型的稳健性。通过实践案例分析，如供应链优化、生产计划与调度以及财务规划，本文展示了Excel线性优化模型的实际应用价值。最后，探讨了Excel线性优化模型的进阶技巧、存在的限制与解决策略，以及模型的维护和更新方法。本文还前瞻了线性优化的未来趋势，并指出了可能的扩展应用方向，例如结合Excel最新功能和其他优化技术。

# 关键字
线性优化；Excel；供应链优化；生产计划；财务规划；敏感性分析

参考资源链接：[线性优化解农业种植问题：蔬菜净收益最大化](https://wenku.csdn.net/doc/62gphke39o?spm=1055.2635.3001.10343)
# 1. 线性优化基础与Excel的契合度

线性优化是运筹学中的一种重要方法，它在计划、决策和资源分配等多个领域有着广泛的应用。而在众多工具中，Excel凭借其易于使用和强大的数据处理能力成为了构建和应用线性优化模型的理想平台。本章将为读者介绍线性优化的基础知识，并探讨Excel如何协助完成优化任务。

## 线性规划问题的定义和数学表达

线性规划问题通常涉及一组线性不等式或等式，以及一个需要最大化或最小化的线性目标函数。在数学表达中，这类问题可以表示为：

minimize    c^T * x
subject to  A * x <= b
            x >= 0

其中，`c` 是目标函数的系数向量，`x` 是决策变量向量，`A` 和 `b` 分别是约束条件的系数矩阵和常数向量。

## 线性优化模型的组成要素

一个线性优化模型通常包括以下几个要素：

- **目标函数**：定义了模型要优化的目标，比如最小化成本或最大化收益。
- **决策变量**：代表模型中的未知数，是需要通过优化计算得出的。
- **约束条件**：限制了决策变量的选择范围，确保解的可行性。

通过将问题的逻辑和数学表达式转化为Excel中的数据和公式，我们能够利用Excel内置的求解器工具来寻找最优解。在后续章节中，我们将详细探讨如何利用Excel的强大功能来实现这一点。

# 2. Excel在构建线性优化模型中的应用

在本章节中，我们将深入探讨如何使用Excel来构建和应用线性优化模型。我们将从理论基础开始，逐步介绍构建过程，并以实际案例分析来加深理解。Excel作为一款强大的电子表格工具，在处理和分析大量数据时具有诸多优势，它内置的求解器功能能够轻松解决线性规划问题，使得构建优化模型变得更加简单和高效。

## 2.1 线性优化模型的理论基础

### 2.1.1 线性规划问题的定义和数学表达

线性规划问题是一种数学优化方法，它涉及到找到一组决策变量的最优值，以最大化或最小化某个线性目标函数，同时满足一组线性不等式或等式约束条件。在数学上，线性规划问题的一般形式可以表示为：

**目标函数:**
\[ \text{Maximize (或 Minimize)} \; Z = c_1x_1 + c_2x_2 + ... + c_nx_n \]

**约束条件:**
\[ a_{11}x_1 + a_{12}x_2 + ... + a_{1n}x_n \leq b_1 \]
\[ a_{21}x_1 + a_{22}x_2 + ... + a_{2n}x_n \leq b_2 \]
\[ \vdots \]
\[ a_{m1}x_1 + a_{m2}x_2 + ... + a_{mn}x_n \leq b_m \]

**非负性约束:**
\[ x_1, x_2, ..., x_n \geq 0 \]

其中，\( Z \) 是目标函数，\( c_1, c_2, ..., c_n \) 是目标函数系数，\( x_1, x_2, ..., x_n \) 是决策变量，\( a_{ij} \) 和 \( b_i \) 是约束系数和常数项，分别对应第 \( i \) 个约束条件中的第 \( j \) 个变量和常数值。

### 2.1.2 线性优化模型的组成要素

线性优化模型由以下几个基本要素组成：

- **决策变量**: 这些是需要确定的量，通常表示为 \( x_1, x_2, ..., x_n \)。在实际问题中，它们可以代表产品数量、货物配额、资源分配比例等。

- **目标函数**: 这是一个线性表达式，表示问题的目标，即要最大化或最小化的量。

- **约束条件**: 这些条件限制了决策变量的取值范围。它们通常以线性不等式或等式的形式存在。

- **非负性约束**: 决策变量不能取负值，这在实际问题中通常意味着不能生产负数的产品或不能拥有负数的资源。

通过这些基本要素的组合，可以构建出反映实际情况的线性优化模型，并求解出最优解。

## 2.2 利用Excel构建线性优化模型

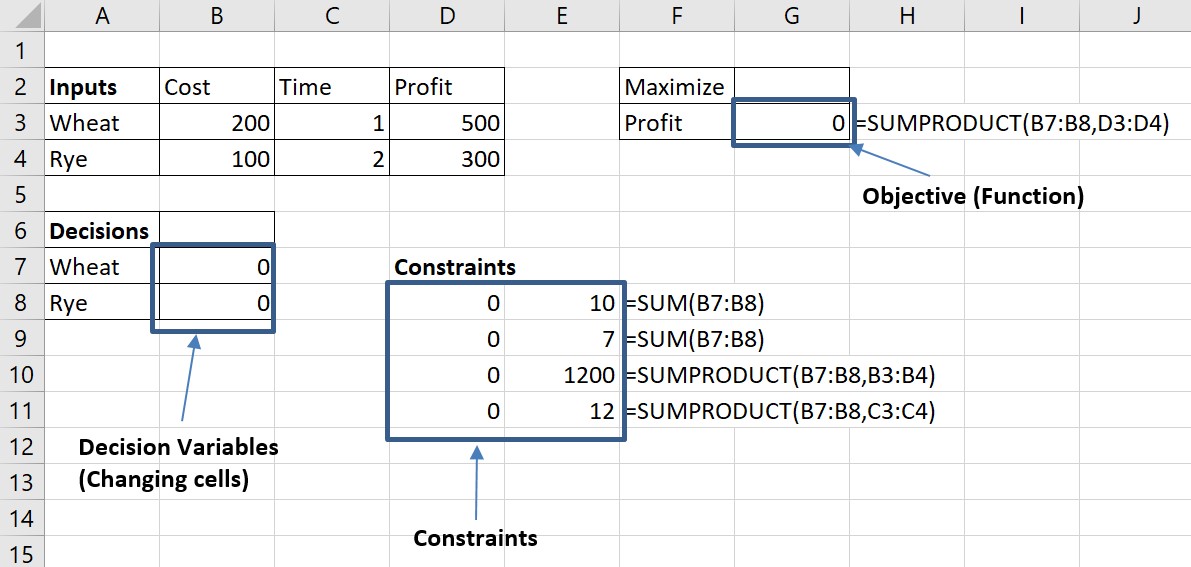
### 2.2.1 设计输入数据表格和决策变量

在Excel中，首先需要设计一个输入数据表格，其中包含模型的所有必要数据。这个表格可以是产品成本、产品需求、资源限制等数据。

接着，需要定义决策变量。在Excel中，决策变量可以是表格中的一个或多个单元格，这些单元格代表优化模型中需要计算得出的值。

### 2.2.2 创建目标函数和约束条件

目标函数和约束条件是线性优化模型的核心部分。在Excel中，它们通常使用单元格引用和公式来表示。

**目标函数**可以通过一个公式来定义，这个公式将引用决策变量的单元格以及它们对应的系数。例如，如果目标是最大化利润，公式可能是 `=SUMPRODUCT(产品利润, 产品数量)`。

**约束条件**则需要使用单元格引用和Excel的函数来构建。例如，如果有一个库存限制，那么可以创建一个公式来确保总产品数量不超过库存限制，形式如 `SUM(产品数量) <= 库存上限`。

### 2.2.3 使用Excel求解器进行优化计算

Excel内置了一个名为“求解器”的工具，它可以用来寻找满足约束条件的目标函数的最大值或最小值。

在使用求解器前，需要先加载这个工具。在Excel选项中，选择“加载项”，并从可用加载项列表中选择“求解器”并确认。

使用求解器时，需要做以下设定：

- 将目标单元格（即包含目标函数的单元格）设置为需要优化的单元格。
- 指定是最大化、最小化还是达到某个目标值。
- 选择决策变量单元格，即那些需要被优化的单元格。
- 添加约束条件，告诉求解器决策变量应该如何被限制。

设置好这些参数后，点击“求解”，Excel将运行求解器算法，寻找满足所有约束条件的目标函数的最优解。

## 2.3 模型结果分析与敏感性分析

### 2.3.1 解释求解器输出结果

求解器完成优化计算后，将给出最优解以及目标函数的最大值或最小值。每个决策变量单元格将显示其对应的最优值。

在模型结果分析中，需要解读这些输出值，并将它们转换为对实际问题的见解。例如，对于一个生产计划问题，输出结果可能表明在特定条件下应生产某种产品的最大数量，以及预期的最大利润。

### 2.3.2 执行敏感性分析以评估模型稳健性

敏感性分析是用来评估模型结果对于参数变化的敏感程度。换句话说，这种分析可以告诉我们当模型的某些参数发生变化时，最优解和目标函数值如何改变。

在Excel中，敏感性分析可以通过观察求解器的“报告”来进行。求解器提供三种类型报告：最终报告、可调报告和极限报告。这些报告揭示了决策变量的值、目标函数的值以及约束条件的变化对整个模型的影响。

通过分析这些报告，我们可以更好地理解模型的稳健性，以及在不确定性和变化的环境中模型的可靠性。

在下一章节中，我们将通过实际案例来展示Excel在线性优化模型构建中的应用，并通过案例分析来进一步深入理解这些概念和技术的应用。

# 3. Excel线性优化的实践案例分析

在本章中，我们将深入探讨Excel线性优化在不同行业中的实际应用案例。通过这些案例，我们可以了解线性优化模型如何解决现实世界中的复杂问题，以及如何利用Excel强大的计算和数据处理能力来实现优化目标。

## 3.1 供应链优化问题

供应链管理是物流、生产和销售等多个环节的综合协调过程。在供应链优化中，通常需要考虑成本、效率和风险等多重因素。Excel线性优化模型能够帮助企业在原料采购、库存管理等方面作出更为精确的决策。

### 3.1.1 原料采购成本与供应量决策模型

一个典型的原料采购成本与供应量决策模型会涉及到多个原料供应商的选择，不同供应商的价格、质量、交货周期和供应能力均不相同。企业需要通过线性优化来确定从各个供应商采购原料的最优量，以实现成本最小化。

**案例背景：**

一家制造企业面临不同供应商提出的原材料采购方案，有三个供应商可供选择，每个供应商都有一系列的供货价格、质量保证和供货周期等条件。

**构建模型步骤：**

1. 设定决策变量，例如：从供应商A、B、C采购的原料量。
2. 定义目标函数，即最小化总采购成本。
3. 设置约束条件，包括每个供应商的最大供货能力、原料的最小需求量、质量标准和交货期限等。

**代码示例：**

=SUMPRODUCT(Costs, Purchases) -> 设定总采购成本为目标函数。

=SUM(A2:A4) <= Supplier_Capacity -> 约束条件，确保采购量不超过供应商的最大供货能力。

**分析与解释：**

通过设定合适的决策变量、目标函数和约束条件，使用Excel求解器可以找到满足所有约束条件的最优解，即最小化总采购成本的同时满足生产需求。最终得出每个供应商的采购量。

**敏感性分析：**

在原料成本或供应链条件发生变动时，通过敏感性分析评估模型的稳健性，即哪些参数变化对总成本影响最大，从而做出应对策略。

### 3.1.2 优化库存管理的Excel解决方案

库存管理是供应链中的另一个关键环节。企业必须保持合理的库存水平，避免过多的库存造成资金占用，或者库存不足导致生产中断。

**案例背景：**

一家零售企业希望优化其库存管理，需要考虑诸如商品的销售速度、存储成本、缺货成本和补货周期等因素。

**构建模型步骤：**

1. 设置决策变量，例如：各种商品的订购量和安全库存量。
2. 定义目标函数，比如最小化总库存成本，包括存储成本和缺货成本。
3. 添加约束条件，如需求量、补货周期和最大存储容量限制等。

**代码示例：**

=SUMPRODUCT(Stocking_Costs, Stock_Levels) + SUMPRODUCT(Stocking_Costs, Safety_Stocks) -> 目标函数，计算总库存成本。

= Inventory * Cycle -> 约束条件，确保库存周期内的需求得到满足。

**分析与解释：**

通过Excel求解器，我们可以得到每个商品的最优订购量和安全库存水平。这样的解决方案有助于企业减少资金占用、降低缺货风险，同时确保顾客满意度。

## 3.2 生产计划与调度问题

在生产制造领域，生产计划和调度问题直接关系到企业的生产效率和成本控制。通过Excel线性优化，企业可以实现生产过程中的最优资源配置。

### 3.2.1 确定最优生产批量和产品组合

生产计划的核心是确定最优的生产批量和产品组合，以满足市场需求，同时最小化生产成本和提高资源利用率。

**案例背景：**

一家工厂有多种产品需要生产，每种产品有其特定的生产周期、原材料消耗、人工成本和市场需求。

**构建模型步骤：**

1. 决策变量包括：各产品的生产量。
2. 目标函数是总生产成本的最小化。
3. 约束条件包括生产能力和市场需求限制。

**代码示例：**

=SUMPRODUCT(Production_Costs, Production_Levels) -> 目标函数，计算总生产成本。

=SUM(Production_Levels) <= Capacity -> 约束条件，确保生产量不超过生产能力。

**分析与解释：**

通过Excel求解器计算，我们可以找到在满足市场需求的同时，使得生产成本最低的最优生产量组合。

### 3.2.2 时间表和资源分配的Excel模型

资源分配问题涉及到生产过程中的劳动力、机器使用、时间等资源的有效分配。

**案例背景：**

一家工厂拥有多条生产线和不同时间段的订单需求，需要根据生产效率和成本制定合理的生产时间表。

**构建模型步骤：**

1. 决策变量包括：各生产线在各个时间段的使用情况。
2. 目标函数是最大化生产效率或最小化生产时间。
3. 约束条件包括劳动力的工作时间、机器的维护时间等。

**代码示例：**

=MAX(SUM(Production_Times)) -> 目标函数，最大化生产线的使用效率。

=SUM(Time_Allocation) <= Working_Hours -> 约束条件，确保工作时间不超过工人的最大工作时间。

**分析与解释：**

求解器将协助优化生产线的使用计划，保证资源得到合理分配，同时满足订单需求。

## 3.3 财务规划与投资组合优化

在金融服务行业，线性优化可用于财务规划和投资组合的优化。其目标是实现风险和回报之间的最佳平衡。

### 3.3.1 资产分配模型与风险最小化

资产分配模型旨在确定如何分配资金到不同的投资渠道，以达到收益最大化和风险最小化的目标。

**案例背景：**

一家投资公司希望为客户提供一个资产分配方案，需要考虑市场趋势、投资回报率和客户的风险承受能力。

**构建模型步骤：**

1. 决策变量为不同投资产品的投资比例。
2. 目标函数是最大化投资组合的预期回报率，同时最小化风险。
3. 约束条件包括投资预算、法律法规限制和客户的风险偏好。

**代码示例：**

=SUMPRODUCT(Returns, Investment_Proportions) -> 目标函数，计算预期回报率。

=VAR.S(Investment_Outcomes) -> 目标函数，计算投资组合的风险值。

**分析与解释：**

通过优化模型，我们可以为客户提供一个既符合其风险偏好又尽可能增加收益的资产分配方案。

### 3.3.2 财务预算的线性优化分析

财务预算的线性优化分析用于确定在有限资源下的最佳开支分配，以确保公司运营的效率和经济性。

**案例背景：**

一个企业希望规划其年度预算，确保各个部门的支出与公司整体的财务目标保持一致。

**构建模型步骤：**

1. 决策变量为各部门的预算分配。
2. 目标函数是最大化公司的整体收益。
3. 约束条件包括总体预算限制、部门间的依赖关系和项目的优先级。

**代码示例：**

=SUM(Dept_Budgets) -> 约束条件，确保总预算不超过公司设定的财务指标。

=SUMPRODUCT(Dept_Benefits, Dept_Budgets) -> 目标函数，计算总收益。

**分析与解释：**

通过Excel求解器，公司可以优化各部门的预算分配，以达成整体财务目标，提升公司的盈利能力。

# 4. Excel线性优化模型的进阶技巧

## 4.1 Excel高级功能在优化模型中的应用

### 4.1.1 使用数组公式简化模型复杂度

数组公式是Excel中一个强大的功能，它允许用户执行对一系列数据的操作，这些操作在传统公式中需要多个步骤来完成。在进行线性优化时，数组公式可以极大地简化模型的复杂度，减少公式数量，提高计算效率。

#### 数组公式示例

假设我们有一个简单的线性优化问题，需要根据一组数据点找到最佳拟合线。以下是一个使用数组公式来计算线性回归的示例：

{=LINEST(A2:A10, B2:B10, TRUE, FALSE)}

在这个例子中，`LINEST`函数是计算线性回归的数组函数。`A2:A10`是x值的范围，`B2:B10`是y值的范围。`TRUE`和`FALSE`分别表示我们希望得到回归统计信息和不希望得到标准误差。按下`Ctrl` + `Shift` + `Enter`将输入数组公式，Excel将在公式栏中将其括在大括号中。

#### 逻辑分析与参数说明

使用数组公式，我们能够一次性对数据进行多个操作，避免了使用循环或多个单独公式，这在处理大型数据集时尤其有用。在上述例子中，`LINEST`函数返回的数组结果包括了斜率、截距和其他回归统计量，这对于线性优化模型中参数的快速求解非常有效。

### 4.1.2 利用VBA自动化优化任务

VBA（Visual Basic for Applications）是Excel的内置编程语言，能够用来创建宏，实现更复杂的操作和自动化任务。在线性优化中，VBA可以用来编写自定义算法，优化模型的求解过程，以及处理复杂的输入输出任务。

#### VBA自动化示例

假设我们需要优化一个包含多个产品的生产计划。我们可以使用VBA编写一个循环来迭代不同的生产组合，寻找成本最低的方案。

Sub OptimizeProduction()
    Dim product As Range
    Dim best组合 As Range
    Dim best成本 As Double
    best成本 = 1E+308
    For Each product In Range("A2:A10")
        ' 计算每个产品的成本和产量
        ' ...
        If total成本 < best成本 Then
            Set best组合 = product
            best成本 = total成本
        End If
    Next product
    ' 输出最优组合到工作表
    best组合.Worksheet.Range("B2").Value = best组合.Value
End Sub

#### 逻辑分析与参数说明

在上述VBA代码中，我们遍历了A2:A10范围内的所有产品，并计算了每种可能的生产组合的成本。然后我们找到成本最低的组合，并将其输出到工作表的特定位置。使用VBA进行自动化，可以有效地处理复杂的逻辑判断和计算过程，提高工作效率。

## 4.2 线性优化模型的限制与解决策略

### 4.2.1 应对非线性问题的线性化方法

线性优化模型的一个主要限制是它仅适用于线性关系。现实世界中的许多问题都具有非线性特征，因此我们需要采用特定的技术将这些问题转换为线性问题，以便可以用线性优化方法来解决。

#### 线性化方法示例

考虑一个需求函数，它是价格的非线性函数。为了线性化，我们可以通过引入二进制变量和线性约束，将非线性函数分解为多个线性部分。

需求 = a - b * 价格

通过引入二进制变量和线性约束，可以将此非线性函数表达为：

需求 = a - b1 * 价格 - b2 * (价格 - 门槛值)

其中，`b1` 和 `b2` 是二进制变量，`门槛值` 是选定的分割点。

#### 逻辑分析与参数说明

线性化过程需要对非线性问题有深刻的理解，并且需要仔细选择二进制变量和适当的分割点。上述线性化方法通过将非线性关系分解为线性部分，允许我们使用线性优化技术来处理原本非线性的问题。这使得原本无法在Excel中处理的复杂模型得以应用线性优化方法解决。

### 4.2.2 数据不准确性和模型的健壮性调整

在实际应用中，线性优化模型通常依赖于大量数据输入，这些数据可能存在不确定性或错误。模型的健壮性对于应对这些问题是至关重要的。

#### 健壮性调整示例

为了提高模型的健壮性，我们可以在模型中引入容错机制，比如使用区间估计替代单点值，或为关键参数设置边界条件。

目标函数：Minimize Σ（成本_i * 变量_i）
约束条件：
    Σ（需求_i * 变量_i） <= Σ（供应_i），对所有产品i
    变量_i >= 下限_i
    变量_i <= 上限_i

在这里，成本、需求、供应以及上限和下限都是不确定的，并且具有一定的变动范围。我们可以通过设置变量的上下限来反映这种不确定性，使得模型在面对不精确数据时依然保持稳健。

#### 逻辑分析与参数说明

在线性优化模型中引入边界条件是一种常见的健壮性调整策略。通过设定参数的上下限，模型能够容纳一定的输入变化，而不是在遇到小的输入变动时就产生大的输出结果变化。这样的调整增强了模型对不确定数据的适应能力，确保了优化结果的可靠性。

## 4.3 模型的维护和更新

### 4.3.1 模型的文档编制和版本控制

随着业务需求的变化，线性优化模型也需要定期更新和维护。良好的文档编制和版本控制可以确保模型的可追溯性和持续改进。

#### 文档编制和版本控制示例

下面是一个简化的模型文档编制和版本控制流程：

1. **模型文档编制** - 详细记录模型的构建、数据源、假设条件和优化目标等关键信息。
2. **版本控制** - 使用Excel的修订功能或版本控制工具记录每次模型的更新和变更历史。

| 版本号 | 更新日期   | 更新人 | 更新内容摘要           |
|--------|------------|--------|------------------------|
| 1.0    | 2023-01-01 | Alice  | 初始模型构建           |
| 1.1    | 2023-02-15 | Bob    | 增加了成本数据          |
| 1.2    | 2023-03-30 | Alice  | 对约束条件进行了调整    |

#### 逻辑分析与参数说明

模型文档编制应详细说明模型的设计原理、数据来源、关键参数和决策逻辑，这对于新用户理解模型和现有用户跟踪模型变更非常有帮助。而版本控制则确保了模型的变更历史可以被追溯，便于团队协作和问题调试。

### 4.3.2 长期维护与动态调整优化模型

为了确保线性优化模型能够适应不断变化的业务需求和环境，模型需要定期进行检查和更新。这种动态的调整可以保持模型的相关性和准确性。

#### 长期维护与动态调整示例

例如，如果我们的生产优化模型需要考虑季节性需求变化，可能需要周期性地更新模型以反映这种变化。

| 季节 | 需求预测 |
|------|----------|
| 春季 | 增加10%  |
| 夏季 | 减少5%   |
| 秋季 | 保持不变 |
| 冬季 | 增加3%   |

在模型中引入季节性调整因子，可以让模型动态地适应需求的波动。

#### 逻辑分析与参数说明

在进行长期维护时，需要关注模型的输出结果是否合理，以及是否需要引入新的约束条件或调整现有的参数。通过动态调整模型，可以保证模型输出的准确性和应用的有效性。对于模型的任何改动都应该通过严格的测试和验证过程来确保其稳健性。

# 5. 线性优化的未来趋势与扩展应用

随着技术的不断进步，优化技术也在持续发展，特别是与新兴技术的结合，为线性优化带来了更多可能性。本章将探讨线性优化技术的最新趋势和扩展应用，包括结合最新Excel版本的新功能以及探索线性优化之外的优化技术。

## 结合最新Excel版本的新功能

### Excel 365与Power Query在数据处理中的应用

Excel 365作为微软推出的一款订阅模式的Office办公软件，其中包含了诸多实用的新功能。Power Query是一个强大的数据准备工具，可用来清洗、转换和加载数据。结合线性优化模型，Power Query可以帮助我们更快地从不同数据源导入数据，进行预处理，并最终整合到优化模型中。

#### 实操步骤：

1. 打开Excel，选择“数据”选项卡中的“获取数据”。
2. 从各种数据源中选择所需的数据源类型，比如从网页、文件、数据库等。
3. 使用Power Query编辑器进行数据清洗和转换。
4. 加载数据到工作表或数据模型中，以便在构建线性优化模型时使用。

### 使用Excel的高级分析工具箱

Excel内置的高级分析工具箱（也称为分析工具库）提供了包括线性规划在内的各种统计分析功能。最新的Excel版本继续扩展了这些工具的功能，提高了它们的计算速度和对复杂问题的处理能力。

#### 实操步骤：

1. 确保在Excel选项中激活了“分析工具库”。
2. 进入“数据”选项卡，在“分析”组中选择“分析工具库”。
3. 选择“规划求解”进行线性优化。
4. 设置目标单元格、目标值、变量单元格、约束条件等。
5. 运行求解器，并查看结果。

## 探索线性优化之外的优化技术

### 约束规划与随机优化技术简介

尽管线性优化在解决资源分配和生产调度等传统问题上表现突出，但它在处理一些实际问题时也遇到了局限性，比如在涉及高度复杂约束或不确定性的场景中。约束规划（Constraint Programming）和随机优化技术（Stochastic Optimization）是两种扩展方法，它们在特定领域内提供了更强的灵活性和适应性。

#### 约束规划

约束规划通过声明式的变量约束、目标函数和搜索策略来解决复杂的优化问题。与线性优化相比，约束规划在问题建模上更加直观和灵活。

#### 随机优化技术

随机优化技术，如模拟退火、遗传算法等启发式算法，用于处理具有不确定性参数的优化问题。这些方法在找到最优解的过程中具有更强的适应性和鲁棒性。

### 机器学习与优化算法的结合

机器学习的兴起为优化算法的发展带来了新的契机。通过训练数据集，机器学习模型可以预测结果并对优化问题提供启发式解。例如，强化学习能够通过学习策略来求解复杂决策问题，神经网络可以用来近似复杂的非线性关系，为优化算法提供更精准的输入。

通过集成机器学习算法，优化模型不仅能够处理更复杂的问题，而且能够进行自我学习和优化，以适应动态变化的环境和条件。这种结合为优化领域打开了新的大门，促进了先进人工智能技术在现实世界问题中的应用。

在本章节中，我们探索了线性优化的未来趋势，以及一些扩展应用。随着技术的演进，我们可以预见线性优化技术将会在与最新工具和算法的结合下，展现出更多强大的应用潜力。这将帮助我们更加高效地解决复杂的现实世界问题。