揭秘MATLAB曲面拟合的7大陷阱：让你的拟合更准确

# 1. MATLAB曲面拟合概述

**1.1 曲面拟合的定义和目的**

曲面拟合是一种数学技术，用于根据一组给定的数据点找到一个曲面，该曲面最能代表数据的趋势。其目的是从有限的数据中推断出数据的潜在规律和关系。

**1.2 MATLAB中曲面拟合的应用**

MATLAB提供了一系列用于曲面拟合的函数和工具，使其成为执行各种曲面拟合任务的理想平台。MATLAB中的曲面拟合可用于：

* 数据可视化和趋势分析
* 模型拟合和预测
* 优化和控制
* 科学和工程中的复杂数据建模

# 2. 曲面拟合的理论基础

### 2.1 曲面拟合的基本原理

曲面拟合是一种通过给定一组数据点，找到一条或多条曲面，以最优地表示这些数据点的过程。其基本原理是：

- **数据点拟合：**寻找一条或多条曲面，使这些曲面尽可能接近给定的数据点。
- **误差最小化：**通过最小化曲面与数据点之间的误差，来确定最优的拟合曲面。
- **模型选择：**根据数据的特点和拟合目的，选择合适的曲面模型，如多项式、指数函数或三角函数等。

### 2.2 常见的曲面拟合方法

MATLAB 提供了多种曲面拟合方法，包括：

| 方法 | 描述 |
|---|---|
| `polyfit` | 多项式拟合 |
| `fit` | 通用拟合，支持多种模型 |
| `csaps` | 样条拟合 |
| `scatteredInterpolant` | 散点插值 |

### 2.3 误差评估和模型选择

拟合曲面的质量可以通过误差评估来衡量，常用的误差指标包括：

- **均方误差 (MSE)**：曲面与数据点之间的平均平方误差。
- **均方根误差 (RMSE)**：MSE 的平方根。
- **最大绝对误差 (MAE)**：曲面与数据点之间最大的绝对误差。

在选择曲面拟合模型时，需要考虑以下因素：

- **数据的分布：**数据的分布决定了合适的模型类型，如线性、非线性或多项式。
- **拟合目的：**拟合曲面的目的是预测、插值还是描述数据趋势。
- **模型复杂度：**模型越复杂，拟合效果越好，但过拟合的风险也越大。

% 导入数据
data = load('data.txt');

% 创建多项式拟合模型
model = polyfit(data(:,1), data(:,2), 2);

% 评估拟合质量
mse = mean((model(1) * data(:,1).^2 + model(2) * data(:,1) + model(3) - data(:,2)).^2);
rmse = sqrt(mse);
mae = max(abs(model(1) * data(:,1).^2 + model(2) * data(:,1) + model(3) - data(:,2)));

% 打印误差评估结果
fprintf('均方误差 (MSE): %.4f\n', mse);
fprintf('均方根误差 (RMSE): %.4f\n', rmse);
fprintf('最大绝对误差 (MAE): %.4f\n', mae);

**代码逻辑分析：**

- 导入数据文件 `data.txt`，其中包含两列数据：自变量 `data(:,1)` 和因变量 `data(:,2)`。
- 使用 `polyfit` 函数创建二次多项式拟合模型 `model`。
- 计算 MSE、RMSE 和 MAE 以评估拟合质量。
- 打印误差评估结果，以了解拟合曲面的准确性。

# 3.1 数据预处理和特征工程

#### 数据预处理

数据预处理是曲面拟合过程中至关重要的一步，它可以提高拟合模型的精度和鲁棒性。数据预处理的主要步骤包括：

- **数据清理：**删除缺失值、异常值和噪声数据。异常值可以显著影响拟合结果，因此需要将其识别并处理。
- **数据标准化：**将数据特征缩放到相同的范围，以防止某些特征对拟合过程产生过大影响。
- **特征选择：**选择与目标变量最相关的特征，以减少模型的复杂度并提高其泛化能力。

#### 特征工程

特征工程是创建新的特征或修改现有特征的过程，以提高模型的性能。常见的特征工程技术包括：

- **特征转换：**将原始特征转换为更适合拟合任务的形式，例如对数转换或二值化。
- **特征组合：**将多个原始特征组合成新的特征，以捕获更复杂的关系。
- **降维：**使用主成分分析 (PCA) 或奇异值分解 (SVD) 等技术减少特征的数量，同时保留最重要的信息。

### 3.2 曲面拟合模型的建立和评估

#### 模型建立

MATLAB 提供了多种曲面拟合模型，包括：

- **多项式回归：**使用多项式函数拟合数据。
- **径向基函数 (RBF) 拟合：**使用径向基函数作为内核函数拟合数据。
- **神经网络：**使用神经网络模型拟合数据。

模型选择取决于数据的性质和拟合任务。

#### 模型评估

模型评估是衡量拟合模型性能的过程。常用的评估指标包括：

- **均方误差 (MSE)：**测量拟合模型和真实数据之间的平均平方误差。
- **决定系数 (R^2)：**表示模型解释数据变异的程度。
- **交叉验证：**将数据分成训练集和测试集，以评估模型的泛化能力。

### 3.3 模型优化和参数调整

#### 模型优化

模型优化旨在找到模型参数的最佳值，以最小化误差。MATLAB 提供了多种优化算法，例如：

- **梯度下降：**使用梯度信息迭代更新模型参数。
- **牛顿法：**使用二阶导数信息加速梯度下降。
- **共轭梯度法：**一种快速收敛的梯度下降变体。

#### 参数调整

模型参数调整是通过调整模型超参数（例如多项式的阶数或 RBF 核函数的带宽）来提高模型性能的过程。超参数调整可以通过网格搜索或贝叶斯优化等技术进行。

# 4. 曲面拟合陷阱及解决方案

在曲面拟合过程中，可能会遇到各种各样的陷阱，影响拟合模型的准确性和鲁棒性。本章节将探讨常见的曲面拟合陷阱及其对应的解决方案。

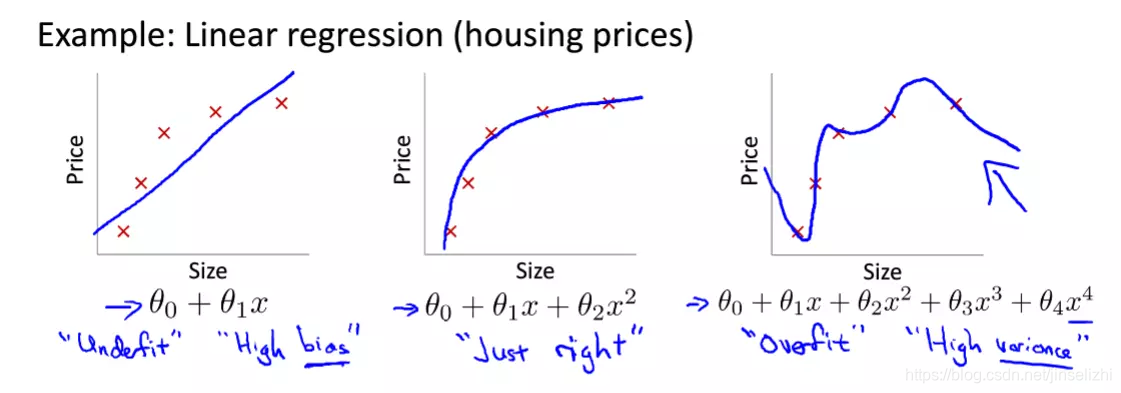
### 4.1 过拟合和欠拟合

**过拟合**是指模型对训练数据拟合得太好，以至于无法泛化到新的数据。这会导致模型在训练集上表现良好，但在测试集上表现不佳。

**欠拟合**是指模型对训练数据拟合得太差，无法捕获数据的潜在模式。这会导致模型在训练集和测试集上都表现不佳。

**解决方案：**

* **正则化：**添加正则化项到损失函数中，以惩罚模型的复杂度。这有助于防止过拟合。
* **交叉验证：**使用交叉验证来评估模型的泛化能力。将训练数据分成多个子集，并使用其中一个子集作为验证集，其余子集作为训练集。通过多次重复此过程，可以获得模型泛化能力的更可靠估计。
* **模型选择：**尝试不同的模型复杂度，并根据验证集上的性能选择最佳模型。

### 4.2 数据噪声和异常值

**数据噪声**是指数据中存在的随机波动，它可能会干扰曲面拟合过程。**异常值**是指与数据集中其他点明显不同的数据点，它们也可能对拟合模型产生负面影响。

**解决方案：**

* **数据预处理：**在拟合模型之前，对数据进行预处理，以去除噪声和异常值。这可以包括平滑、滤波和剔除异常值。
* **稳健回归：**使用稳健回归算法，这些算法对异常值不敏感。
* **M估计：**使用M估计，它是一种对异常值鲁棒的估计方法。

### 4.3 协线性问题

**协线性**是指自变量之间存在高度相关性。这会导致模型不稳定，并且难以解释模型系数。

**解决方案：**

* **特征选择：**选择一组非共线的特征，以构建模型。
* **正则化：**使用正则化项，以惩罚模型中协线性特征的系数。
* **主成分分析 (PCA)：**使用PCA将协线性特征投影到一组正交主成分上。

### 4.4 模型复杂度选择

**模型复杂度**是指模型中参数的数量。模型复杂度过高会导致过拟合，而模型复杂度过低会导致欠拟合。

**解决方案：**

* **交叉验证：**使用交叉验证来选择最佳模型复杂度。
* **AIC 和 BIC：**使用赤池信息准则 (AIC) 或贝叶斯信息准则 (BIC) 来评估模型复杂度。AIC 和 BIC 会惩罚模型复杂度，从而有助于选择最优模型。

**代码示例：**

% 使用交叉验证选择正则化参数lambda
lambda_values = [0.01, 0.1, 1, 10, 100];
mse_values = zeros(size(lambda_values));

for i = 1:length(lambda_values)
    lambda = lambda_values(i);
    % 训练模型
    model = fitlm(X, y, 'Linear', 'Lambda', lambda);
    % 计算交叉验证均方误差
    mse_values(i) = crossval('mse', X, y, 'Model', model);
end

% 选择具有最小交叉验证均方误差的lambda值
[min_mse, min_index] = min(mse_values);
lambda_opt = lambda_values(min_index);

# 5. MATLAB曲面拟合高级应用

### 5.1 多维曲面拟合

在现实世界中，数据通常具有多个维度。多维曲面拟合涉及拟合具有多个自变量的高维曲面。MATLAB提供了用于多维曲面拟合的函数，例如 `fitnlm` 和 `fitrnet`。

% 生成三维数据
x = linspace(-1, 1, 100);
y = linspace(-1, 1, 100);
[X, Y] = meshgrid(x, y);
Z = X.^2 + Y.^2;

% 多维曲面拟合
model = fitnlm([X(:), Y(:)], Z(:), 'quadratic');

% 评估模型
rmse = sqrt(mean((Z(:) - predict(model, [X(:), Y(:)])).^2));
disp(['RMSE: ', num2str(rmse)]);

### 5.2 非线性曲面拟合

非线性曲面拟合涉及拟合非线性关系。MATLAB提供了用于非线性曲面拟合的函数，例如 `fminsearch` 和 `fminunc`。

% 定义非线性函数
f = @(x) x.^3 - 2*x + 1;

% 非线性曲面拟合
x0 = 0;  % 初始猜测
options = optimset('Display', 'iter');  % 显示迭代信息
[x_opt, fval] = fminsearch(f, x0, options);

% 评估模型
disp(['最优值: ', num2str(x_opt)]);
disp(['函数值: ', num2str(fval)]);

### 5.3 曲面拟合在工程和科学中的应用

曲面拟合在工程和科学中有着广泛的应用，包括：

- **工程设计：**优化飞机机翼形状、汽车底盘设计等。
- **科学建模：**模拟物理现象、化学反应等。
- **医学成像：**重建三维器官模型、诊断疾病等。
- **金融预测：**预测股票价格、汇率等。