MATLAB曲面拟合模型评估秘籍：度量拟合质量的5大指标

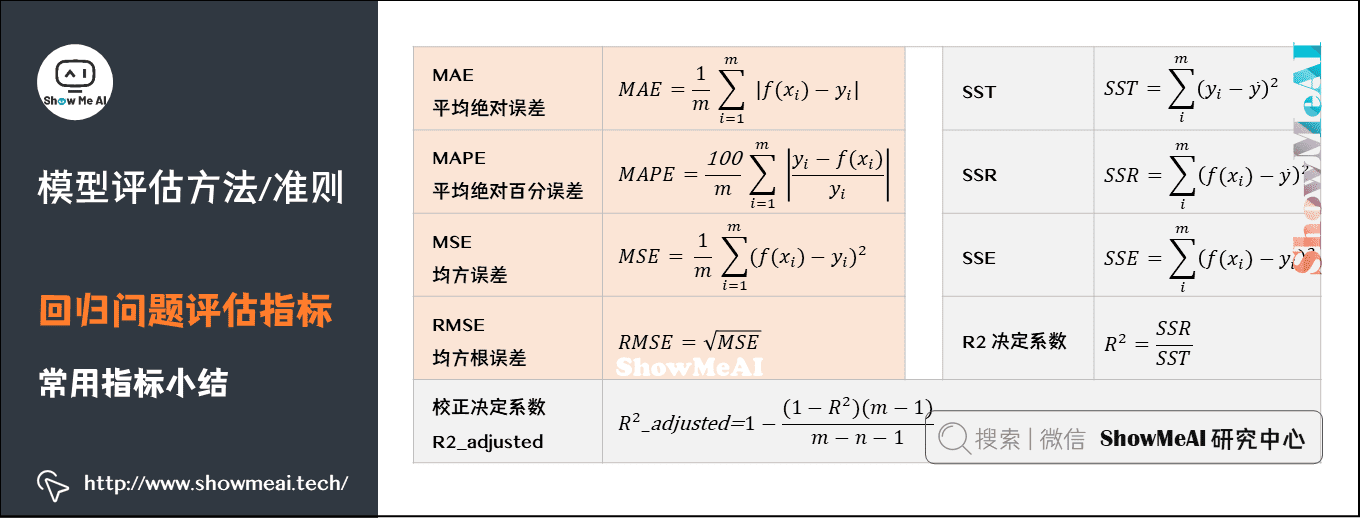
# 1. MATLAB曲面拟合概述**

曲面拟合是一种通过数学函数近似表示一组数据点的技术。在MATLAB中，可以通过`fit`函数执行曲面拟合。`fit`函数接收数据点和一个函数模型作为输入，并返回一个拟合对象，其中包含拟合函数的参数和相关统计信息。

曲面拟合在各种应用中非常有用，例如：

- 数据可视化：通过将数据拟合到曲面上，可以更直观地展示数据的趋势和模式。
- 数据预测：拟合的曲面可用于预测新数据的行为，从而支持决策和规划。
- 模型开发：曲面拟合可用于开发预测模型，这些模型可以用于各种目的，例如优化和控制。

# 2. 曲面拟合质量评估指标

### 2.1 拟合优度指标

拟合优度指标衡量拟合模型与原始数据的匹配程度。常用的拟合优度指标包括：

#### 2.1.1 均方根误差（RMSE）

RMSE 衡量预测值与真实值之间的平均差异。RMSE 越小，拟合效果越好。

RMSE = sqrt(1/n * Σ(y_i - y_hat_i)^2)

其中：

* n 为数据点数
* y_i 为真实值
* y_hat_i 为预测值

#### 2.1.2 平均绝对误差（MAE）

MAE 衡量预测值与真实值之间的平均绝对差异。MAE 越小，拟合效果越好。

MAE = 1/n * Σ|y_i - y_hat_i|

#### 2.1.3 确定系数（R²）

R² 衡量拟合模型解释数据变异的程度。R² 越接近 1，拟合效果越好。

R² = 1 - Σ(y_i - y_hat_i)^2 / Σ(y_i - y_bar)^2

其中：

* y_bar 为真实值的平均值

### 2.2 残差分析指标

残差分析指标衡量拟合模型的误差分布。常用的残差分析指标包括：

#### 2.2.1 残差图

残差图显示预测值与真实值之间的差异。理想情况下，残差图应呈现随机分布，无明显模式。

#### 2.2.2 残差分布直方图

残差分布直方图显示残差的分布情况。理想情况下，残差分布应接近正态分布，无明显偏态或峰度。

#### 2.2.3 自相关图

自相关图显示残差之间的相关性。理想情况下，自相关图应无明显模式，表明残差之间无相关性。

# 3. 曲面拟合模型评估实践

### 3.1 模型拟合与评估流程

曲面拟合模型评估是一个系统化的过程，涉及以下步骤：

**3.1.1 数据预处理**

* **数据清理：**删除异常值和缺失数据。
* **数据标准化：**将数据缩放或中心化，以提高拟合算法的效率。
* **特征工程：**提取相关特征或创建新特征，以增强模型的预测能力。

**3.1.2 模型训练和拟合**

* **模型选择：**根据数据的特征和拟合目标，选择合适的曲面拟合模型。
* **模型训练：**使用训练数据集训练模型，调整模型参数以最小化损失函数。
* **模型拟合：**将训练好的模型应用于测试数据集，评估模型的拟合优度。

**3.1.3 模型评估**

* **拟合优度指标：**使用RMSE、MAE和R²等指标评估模型的预测精度。
* **残差分析指标：**使用残差图、残差分布直方图和自相关图分析模型的拟合质量。
* **交叉验证：**使用k折交叉验证或留一法交叉验证，评估模型的鲁棒性和泛化能力。

### 3.2 不同指标的应用场景

**3.2.1 预测精度评估**

* **RMSE：**衡量预测值与实际值之间的平均误差，适用于预测连续变量。
* **MAE：**衡量预测值与实