递归算法在数据结构中的角色：实现栈和队列的递归方法


参考资源链接：[递归算法求解传染病问题](https://wenku.csdn.net/doc/6412b75bbe7fbd1778d4a00d?spm=1055.2635.3001.10343)
# 1. 递归算法基础

递归算法是计算机科学中解决问题的一种基本方法，它通过函数自我调用来简化问题的解决步骤。在这一章节中，我们将从递归算法的基础概念入手，逐步深入探讨其核心原理和应用场景。

## 1.1 递归的定义和原理

递归算法的核心思想是将大问题分解为小问题，直到达到一个简单的基础情况，该情况可以直接解决。然后，通过解决所有小问题来组合出大问题的解决方案。

例如，计算一个数的阶乘可以定义为 `n! = n * (n-1)!`，其中 `1! = 1` 是基础情况。递归算法的代码实现通常包含两个基本要素：
- 基础情况（Base Case）：算法的最简单形式，避免无限递归。
- 递归情况（Recursive Case）：将问题分解成更小的子问题，并递归调用函数自身。

代码示例（Python）：

def factorial(n):
    if n == 1:  # 基础情况
        return 1
    else:  # 递归情况
        return n * factorial(n - 1)

print(factorial(5))  # 输出: 120

## 1.2 递归与问题解决

递归算法特别适用于处理那些可以自然分解为相似子问题的问题。它能够简化代码的复杂性，但同时也带来了一些挑战，如栈溢出、效率低下等。在接下来的章节中，我们将探讨如何有效地实现和优化递归算法，以及它在不同领域的实际应用。

# 2. 递归与栈的实现

## 2.1 栈的数据结构概述

### 2.1.1 栈的定义和基本操作

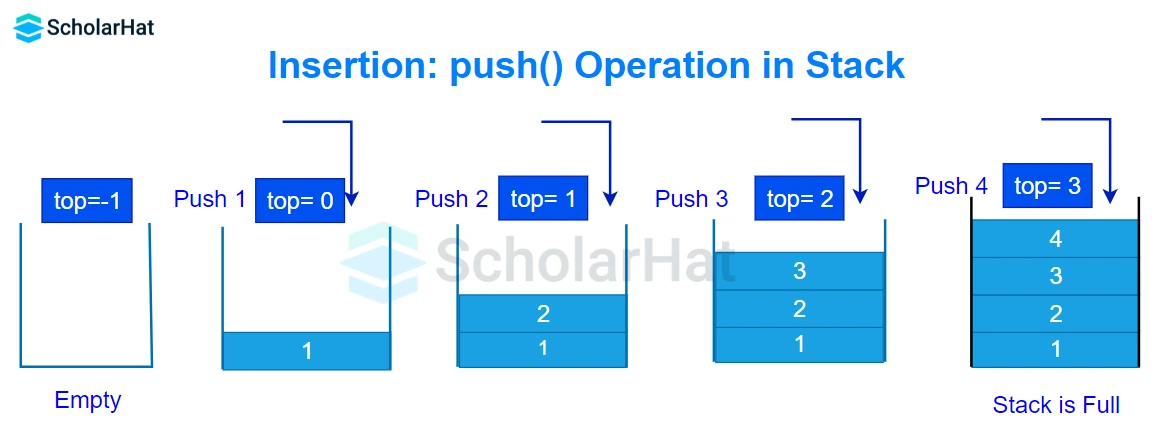
在计算机科学中，栈是一种遵循后进先出（LIFO, Last In First Out）原则的数据结构。在栈中，新加入的元素被存放在栈的顶部，而取元素则只能从栈顶开始，这也被称为“推入（Push）”和“弹出（Pop）”操作。这两个操作保证了在任何时候，只有最后一个被“推入”的元素可以被“弹出”。

- **基本操作包括**：
- **推入（Push）**：将一个数据项添加到栈的顶部。
- **弹出（Pop）**：移除栈顶的数据项，并返回它。
- **查看栈顶（Peek）**：查看栈顶的数据项但不移除它。
- **检查是否为空（IsEmpty）**：检查栈是否为空。
- **清空栈（Clear）**：移除栈内的所有元素。

### 2.1.2 栈的递归实现原理

递归是实现栈操作的一种自然方式，因为它本质上就是函数调用自身，符合栈的后进先出特性。递归实现的每个函数调用都相当于压入一个栈帧，每个栈帧包含了该次调用的状态和局部变量，当一个函数结束时，它会将控制权返回给前一个栈帧，直到所有栈帧都被清空。

递归实现栈的一个关键点是使用系统栈来维护函数调用状态，这意味着每一次函数调用都会创建一个栈帧并将其放在系统栈上。例如，在递归函数中，每次调用自身时，新的调用都会在系统栈上创建一个新的栈帧。

下面是一个简单的递归实现的栈结构的示例代码：

class Node:
    def __init__(self, value):
        self.value = value
        self.next = None

class Stack:
    def __init__(self):
        self.top = None
    def push(self, value):
        new_node = Node(value)
        new_node.next = self.top
        self.top = new_node
    def pop(self):
        if self.is_empty():
            return None
        popped_node = self.top
        self.top = self.top.next
        return popped_node.value
    def is_empty(self):
        return self.top is None

在上述代码中，`push` 方法和 `pop` 方法都是递归地访问和操作栈顶元素。`push` 方法将新节点添加到栈顶，而 `pop` 方法则移除栈顶元素。要注意的是，由于我们使用了递归，因此需要设定一个递归结束的条件。例如，在 `pop` 方法中，当栈为空时，我们没有节点可弹出，递归将结束。

## 2.2 栈的递归应用案例

### 2.2.1 递归实现汉诺塔问题

汉诺塔问题是一个经典的递归问题，目标是将所有盘子从一个塔移动到另一个塔上，且在移动过程中必须遵守以下规则：

- 每次只能移动一个盘子。
- 盘子只能从塔顶移动到另一个塔顶。
- 在移动过程中，较大的盘子不能叠在较小的盘子上面。

汉诺塔问题可以递归地解决，通过将较大的盘子移动到辅助塔，然后将较小的盘子移动到目标塔，最后将大的盘子从辅助塔移动到目标塔。下面是一个递归解法的示例：

def hanoi(n, source, target, auxiliary):
    if n == 1:
        print(f"Move disk 1 from {source} to {target}")
        return
    hanoi(n-1, source, auxiliary, target)
    print(f"Move disk {n} from {source} to {target}")
    hanoi(n-1, auxiliary, target, source)

# 调用函数
hanoi(3, 'A', 'C', 'B')

### 2.2.2 递归解决括号匹配问题

括号匹配是编程语言中常见的一种结构，目的是检查一个字符串中的括号是否正确匹配。例如，在字符串 "((()))" 中，括号是匹配的，而在字符串 "(()" 中则不是。

递归方法可以检查括号匹配问题，通过递归地处理字符串的每个字符，每次遇到左括号时将其压入栈，遇到右括号时检查栈顶是否有对应的左括号，有则弹出，否则说明括号不匹配。

def is_parentheses_balanced(expression):
    stack = []
    parentheses_map = {')': '(', '}': '{', ']': '['}
    for char in expression:
        if char in parentheses_map.values():
            stack.append(char)
        elif char in parentheses_map.keys():
            if stack == [] or parentheses_map[char] != stack.pop():
                return False
        else:
            return False  # 非括号字符会使匹配失败
    return stack == []

# 测试函数
print(is_parentheses_bal