递归算法在优化问题中的应用：找到传染病问题的最优解


参考资源链接：[递归算法求解传染病问题](https://wenku.csdn.net/doc/6412b75bbe7fbd1778d4a00d?spm=1055.2635.3001.10343)
# 1. 递归算法与优化问题

## 1.1 递归算法概述
递归算法是一种在解决问题时调用自身的算法策略，它将复杂问题分解为更小的相似子问题，直至达到基本情况（base case），从而得到问题的解。递归的方法为程序员提供了一种简洁的编码方式，尤其在处理树形数据结构和一些自然分层的问题时，递归的表达能力强大且直观。

## 1.2 递归与迭代的比较
递归与迭代是实现算法的两种不同方法。递归的代码通常更易于理解，因为它直接反映了问题的数学模型。然而，递归可能会导致大量的函数调用，从而消耗更多的内存资源。相比之下，迭代通过循环结构重复使用同一变量，通常具有更高的空间效率。在实际应用中，选择递归还是迭代取决于问题的具体情况和性能需求。

## 1.3 递归深度的限制与优化
在某些情况下，如深度递归调用时，可能会遇到栈溢出的问题，这是因为每个递归调用都会占用一定的栈空间，而计算机的栈空间是有限的。为了解决这一问题，可以进行递归深度的限制与优化，例如将递归改为迭代，使用尾递归优化技术，或是在函数调用前检测栈空间是否足够等策略。

import sys

sys.setrecursionlimit(3000)  # 增加递归深度限制

以上代码示例展示了如何通过Python的sys模块增加递归深度限制。然而，更重要的是理解算法本身的优化，以减少实际需要的递归深度，这将在后续章节中详细介绍。

# 2. 递归算法的理论基础

### 2.1 递归的定义与特性

递归是一种常见的编程技术，它允许函数调用自身以解决问题。递归函数的定义包括两个主要部分：基本情况和递归情况。基本情况是递归结束的条件，通常是一个简单的实例，可以直接解决而不需要进一步的递归调用。递归情况则是函数调用自身来处理问题的子集，这个过程会不断重复，直到达到基本情况。

#### 2.1.1 递归的基本概念

递归函数通常包括以下几个要素：

1. **终止条件（Base Case）**：确定何时停止递归。
2. **递归步骤（Recursive Step）**：定义问题如何分解为更小的同类问题。
3. **递归表达式**：函数调用自身来解决问题的更小实例。

递归是一种强大而灵活的编程方法，可以简化代码结构，减少冗余，但同时它可能引入高复杂度和栈溢出的风险。

#### 2.1.2 递归与迭代的比较

递归与迭代是解决问题的两种不同方法。递归通过分解问题并使用自身函数解决子问题来工作，而迭代则是通过循环结构重复执行操作直至完成。

| 特点 | 递归 | 迭代 |
| --- | --- | --- |
| **理解复杂度** | 可能更直观，尤其对于分层或自然分解的问题 | 通常更简单，逻辑更加直接 |
| **性能开销** | 函数调用可能导致额外的性能开销 | 循环控制通常比函数调用更高效 |
| **资源消耗** | 可能导致栈溢出，特别是深层递归 | 通常占用更少的内存资源 |
| **代码简洁性** | 代码更简洁，易于编写 | 可能需要更复杂的控制逻辑 |

在选择递归还是迭代时，需要根据具体问题的性质和资源限制来决定。递归在解决某些类型的问题（如树遍历、分治策略）时更为直观和方便，而迭代则在处理简单的循环逻辑时更为高效。

### 2.2 递归算法的数学模型

#### 2.2.1 概率模型在递归算法中的应用

概率模型在递归算法中的应用十分广泛，尤其是在处理具有随机性质的问题时，例如在模拟、预测、风险分析等领域。递归与概率模型相结合，可以通过构建递归树来模拟不同的概率场景，并求解预期结果。

一个典型的例子是递归与马尔可夫链的结合，马尔可夫链是一种描述状态转移概率的模型，当状态转移过程可递归表示时，可以利用递归算法来计算长期均衡分布等概率性质。

#### 2.2.2 递归模型与动态规划

动态规划是解决多阶段决策问题的一个有力工具，其思想基于将复杂问题分解为简单子问题，并存储这些子问题的解以避免重复计算。递归模型与动态规划有天然的联系，因为动态规划本质上是利用递归关系式进行优化。

在动态规划中，递归关系式定义了问题的最优子结构，而记忆化技术可以用于存储已经解决的子问题的解，从而避免不必要的重复计算，大大提高了算法的效率。

### 2.3 递归算法的效率分析

#### 2.3.1 时间复杂度与空间复杂度

递归算法的效率分析主要是基于时间和空间复杂度的考量。时间复杂度反映了算法执行所需的时间量，而空间复杂度则反映了算法执行所需的存储空间。

递归算法的时间复杂度通常为O(n)，其中n是问题规模。但是，由于递归函数的调用堆栈，空间复杂度会是O(n)。在递归深度很大时，这可能导致栈溢出。

递归算法的优化通常包括减少不必要的递归调用（例如通过剪枝技术），或者将递归转换为迭代形式来减少栈空间的使用。

#### 2.3.2 递归深度的限制与优化

递归深度是指递归调用的最大层数。在实际应用中，过深的递归可能导致栈溢出错误。因此，了解并优化递归深度是递归算法实现的关键。

限制递归深度的一种方法是通过引入剪枝技术，即在递归过程中，根据特定条件提前终止某些递归分支的执行。另一种方法是使用尾递归优化技术，在函数调用自身作为最后一个操作时，编译器或解释器可以优化这个递归过程，避免增加新的栈帧，从而减少栈空间的使用。

以上章节内容详细介绍了递归算法的理论基础，包括递归的定义、特性、数学模型的应用以及效率分析。为了使内容连贯，下一章节将探讨递归算法在传染病模型中的应用，这不仅有助于理解理论，也展示了递归在实际问题中的应用价值。

# 3. 递归算法在传染病模型中的应用

## 3.1 传染病模型简介

### 3.1.1 SIR模型及其变种

传染病模型是理解和预测疾病传播的数学工具。其中，最基础也是最著名的模型是SIR模型。SIR模型将人群分为三个相互作用的组别：易感染者（Susceptible）、感染者（Infectious）和移除者（Removed），分别对应S、I和R三个状态。该模型通过一组微分方程来模拟个体在不同状态间的转移，从而对传染病的传播动态进行预测。

SIR模型的基本方程为：

- dS/dt = -βSI/N
- dI/dt = βSI/N - γI
- dR/dt = γI

其中，β表示感染率，γ表示恢复率，N表示总人口数。通过这些方程，我们可以构建出传染病的传播图景，包括疫情的爆发、传播、终止等阶段。

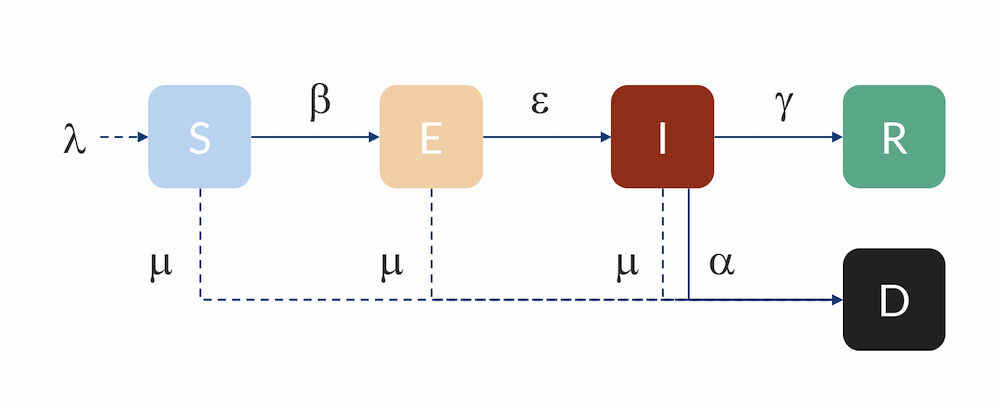
由于SIR模型只关注三种状态，它不能够捕捉到所有类型的疾病传播特点，于是诞生了诸多变种模型，比如SIRS模型增加了重新易感的概念，SEIR模型则在SIR的基础上增加了潜伏者（Exposed）这一类别，用于描述感染后尚未传染给他人的阶段。

### 3.1.2 模型参数的重要性

模型参数对于SIR模型的结果至关重要。感染率β和恢复率γ的变化直接影响着传染病的传播速度和范围。在真实的疫情分析中，这些参数往往基于实际数据进行估计，并且它们可能随着时间和环境条件的变化而变化。

比如，在COVID-19疫情中，不同地区的β值就随着人口密度、公共卫生措施的严格程度、民众的防疫意识等因素而表现出很大差异。因此，准确估计和动态调整这些参数是传染病模型预测准确性的关键。

## 3.2 递归算法求解传染病模型

### 3.2.1 递归框架的构建

递归框架可以用于求解传染病模型中的某些特定问题，尤其是那些涉及多个时间步长或复杂状态转移的问题。递归框架的构建首先需要定义递归方程，然后通过递归调用来计算每个时间点的S、I和R值。

递归的基本思路是，给定当前的S、I、R值，根据感染率和恢复率计算下一个时间步长的状态值。这可以表示为：

def sir_recursive(S, I, R, beta, gamma, time_step):
    if time_step == 0:
        return S, I, R
    new_S = S - beta * S * I / N
    new_I = I + beta * S * I / N - gamma * I
    new_R = R + gamma * I
    return sir_recursive(new_S, new_I, new_R, beta, gamma, time_step - 1)