【R语言专家级教程】：princomp包参数调优的深度解读

# 1. R语言与princomp包概览

## 1.1 R语言简介
R语言是一个用于统计计算和图形表示的强大编程语言和软件环境。它在数据挖掘、机器学习以及生物信息学等领域中广泛应用。R语言因其开源、灵活性以及丰富的包支持而备受专业人士青睐。

## 1.2 princomp包的用途和重要性
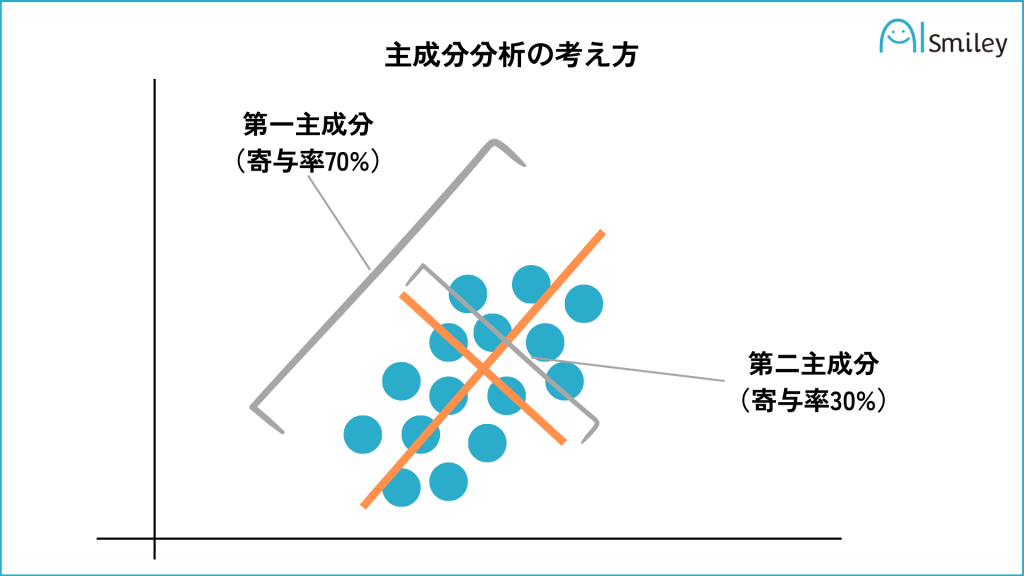
princomp包是R语言中用于执行主成分分析(PCA)的重要工具包之一。PCA是一种常用于数据降维的技术，它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量。在princomp包的帮助下，用户可以方便地处理数据集，识别数据中的主要变化趋势，以及对数据进行可视化解释。

## 1.3 如何安装和加载princomp包
在R环境中，princomp包可以通过以下命令进行安装和加载：

# 安装princomp包（如果尚未安装）
install.packages("princomp")

# 加载princomp包
library(princomp)

通过以上步骤，用户即可开始使用princomp包进行主成分分析了。

# 2. princomp包的统计学基础

### 2.1 主成分分析(PCA)的数学原理

#### 2.1.1 协方差矩阵的概念及其计算

主成分分析（PCA）是多元统计分析中的一种常用技术，它通过正交变换将一组可能相关的变量转换为一组线性不相关的变量，这些新变量称为主成分。在数学表示上，PCA试图在k维空间中寻找数据的最佳表示，通常这个k远小于原始数据的维度。

协方差矩阵是PCA中不可或缺的一个数学工具，它能够描述随机变量之间的线性关系。假设有一个随机变量矩阵X，其中包含了n个观测值，每一行代表一个观测，每一列代表一个变量。协方差矩阵C可以通过下面的公式进行计算：

C = (1/n) * X^T * X

在这里，X^T代表矩阵X的转置，而乘以(1/n)是为了得到无偏估计。

在R语言中，使用princomp包的`covmat`参数可以直接计算数据的协方差矩阵。例如：

# 假设数据集为 dataset
cov_matrix <- princomp(dataset, covmat = TRUE)$covmat

#### 2.1.2 特征值与特征向量的意义

特征值与特征向量是PCA中用于确定主成分的重要数学概念。它们是协方差矩阵的固有属性，描述了矩阵在特定方向上的伸缩程度和方向。

- **特征值**：表示一个主成分的方差大小，可以理解为该方向上数据分布的离散程度。特征值越大，说明该主成分包含的信息越多。
- **特征向量**：与特征值相对应，指示了数据在各个主成分上的展开方向。

在R中，使用princomp函数得到的主成分分析结果中包含了特征值和特征向量的信息。以下是如何提取特征值和特征向量的代码示例：

# 执行主成分分析
pca_result <- princomp(dataset)

# 提取特征值
eigen_values <- pca_result sürek

# 提取特征向量
eigen_vectors <- pca_result vectors

### 2.2 princomp包在PCA中的应用

#### 2.2.1 princomp函数的基本用法

princomp包提供了用于执行PCA的函数`princomp`，其基本用法涉及指定数据集和一些可选参数，如`cor`，`scores`和`center`等。`cor`参数指示是否使用数据集的相关矩阵代替原始数据矩阵进行分析，`scores`参数决定是否返回主成分得分。

例如，对一个数据集进行PCA分析的基本步骤如下：

# 加载数据集
data(iris)

# 执行PCA分析
pca_model <- princomp(iris[, 1:4], cor = TRUE)

# 查看PCA分析结果
summary(pca_model)

在上述示例中，我们使用了鸢尾花数据集（iris dataset）的前四列，这是因为PCA分析通常需要对数值型数据进行。

#### 2.2.2 参数选择对分析结果的影响

在使用princomp函数时，参数的选择至关重要，因为它们将影响最终的分析结果。例如，`cor`参数决定是否将数据标准化。通常在数据变量具有不同量纲或数量级时，我们会选择标准化以避免大数量级的变量对结果产生过大的影响。参数`scores`的使用也很关键，它允许我们查看每个观测在每个主成分上的得分。

参数的选择将直接影响PCA结果的解释性和后续分析。例如，如果我们不使用标准化，那么数据中数值范围大的变量可能会主导协方差矩阵，从而影响主成分的计算。选择是否包含`scores`影响我们能否得到每个样本点的主成分得分，这对于后续的数据可视化和解释非常重要。

### 2.3 PCA结果的解释与可视化

#### 2.3.1 主成分的解释性

在进行PCA后，解释主成分变得至关重要。每个主成分都是原始数据中若干变量的线性组合。主成分的解释性主要依据其特征向量中的系数，系数的绝对值越大，说明在该主成分上该变量的作用越显著。

主成分的解释通常需要领域专家的知识，但也有统计方法如“碎石图”来辅助决策哪些主成分应该被保留。例如，在R中，我们可以通过以下方式绘制“碎石图”：

# 绘制碎石图
plot(pca_model, type = "lines")

通过查看碎石图，我们可以找到特征值开始平坦的地方，这些位置之后的主成分可能不那么重要。

#### 2.3.2 结果的可视化展示方法

PCA结果的可视化是帮助我们理解数据结构和模式的有效手段。最常用的可视化方法包括散点图和气泡图，它们可以帮助我们识别数据中的聚类和异常点。

使用R中的`biplot`函数可以生成一个包含了样本点和变量方向的图表：

# 绘制biplot
biplot(pca_model)

在`biplot`中，样本点的位置表示它们在主成分空间中的位置，而向量则指向原始变量的方向。这可以帮助我们理解哪些变量对哪些主成分有较大的贡献。

mermaid流程图是一个特别有用的工具，用于可视化PCA结果，尤其是当涉及到复杂的数据结构时。然而，由于PCA本身是一个统计过程，mermaid的直接应用较少。不过，mermaid可以被用于显示PCA分析后的数据结构，比如通过描述PCA后如何进行聚类分析。以下是一个简单的mermaid流程图，描述了一个PCA后数据聚类的流程：

graph LR
A[开始PCA分析] --> B[计算协方差矩阵]
B --> C[计算特征值和特征向量]
C --> D[确定主成分]
D --> E[根据特征值选择主成分]
E --> F[计算数据集的主成分得分]
F --> G[可视化结果]
G --> H[分析与解释]

上述流程图虽然不直接用于PCA过程，但它展示了从P