【数据预处理的艺术】：用princomp包优化主成分分析的前奏

# 1. 主成分分析的理论基础

## 1.1 主成分分析的定义
主成分分析（PCA）是一种统计方法，用于将数据集的变量转换为一组线性不相关的变量，称为主成分。这是通过正交变换实现的，转换后的变量称为主成分。在高维数据集分析中，主成分分析帮助减少数据集的维度，同时保留大部分的数据变异性。

## 1.2 主成分分析的目的
PCA的主要目的是降维。在数据科学和机器学习中，拥有大量特征（或维度）的复杂数据集可能导致模型难以解释，计算成本高昂，并且容易过拟合。通过保留原始数据中的重要特征，同时去除冗余特征，PCA提高了数据的可操作性和可解释性。

## 1.3 主成分分析的工作原理
PCA通过找出数据方差最大的方向来工作，每个方向定义为一个主成分。第一个主成分与数据的最大方差对应，第二个主成分与剩余方差的最大值对应，并且与第一个主成分正交，以此类推。通过这种方式，PCA能够将原始数据转换到新的坐标系统中，其坐标轴由这些主成分构成。

# 2. 数据预处理的重要性与方法

## 2.1 数据清洗

### 2.1.1 缺失值处理

在真实世界的数据集中，数据缺失是常见问题。处理缺失值是数据清洗阶段的重要任务，因为缺失值会严重影响后续数据挖掘和分析的效果。常见的处理方法包括：

- 删除含缺失值的记录。适用于缺失值不多的情况。
- 填充缺失值，比如使用均值、中位数、众数或预测模型估计值填充。
- 利用模型或算法直接处理缺失值，如使用支持向量机(SVM)或随机森林。

例如，在R语言中使用均值填充缺失值，可以使用以下代码：

# 假设data为数据框，且其中含有缺失值
for (i in 1:ncol(data)) {
  data[ , i][is.na(data[ , i])] <- mean(data[ , i], na.rm = TRUE)
}

上述代码逐列遍历数据框`data`，对每一列中含有NA值的元素，用该列的均值替代。使用均值填充是一种简单方法，但在数据不符合正态分布或者缺失值过多时，效果可能不佳。

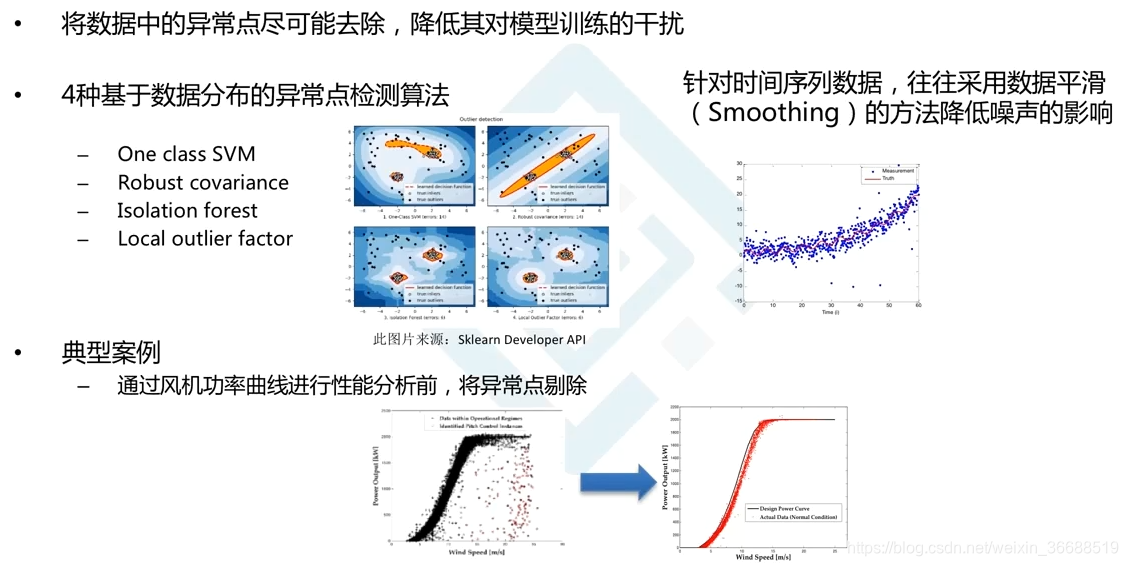
### 2.1.2 异常值检测与处理

异常值是显著偏离其他观测值的数据点，可能由错误、测量误差或其他异常情况引起。异常值的检测和处理对数据质量和后续分析至关重要。异常值的处理方法包括：

- 删除异常值。
- 使用箱型图、Z-score或基于统计学的方法来识别异常值。
- 进行数据变换，例如对数变换、Box-Cox变换等。

例如，在R中使用Z-score方法检测异常值的代码如下：

# 计算每列的Z-score
z_scores <- scale(data)

# 定义异常值的标准，例如超过3个标准差
outliers <- abs(z_scores) > 3

# 将异常值替换为NA
data[outliers] <- NA

# 处理异常值，例如用均值替代
data[ , ] <- apply(data, 2, function(x) {
  x[is.na(x)] <- mean(x, na.rm = TRUE)
  return(x)
})

在该示例中，`scale`函数计算了数据的标准化Z-score，随后根据阈值确定并处理了异常值。

## 2.2 数据标准化与归一化

### 2.2.1 标准化的方法

数据标准化是数据预处理的重要环节，旨在消除不同变量之间的尺度影响，使得分析更加准确。标准分数（Z-score）标准化是最常用的一种方法，其计算公式为：

\[ Z = \frac{(X - \mu)}{\sigma} \]

其中，\(X\) 是原始数据，\(\mu\) 是均值，\(\sigma\) 是标准差。

例如，在Python中使用pandas库标准化数据的代码如下：

import pandas as pd

# 假设df为pandas DataFrame，并且我们需要标准化df中的所有列
df_standardized = (df - df.mean()) / df.std()

# df_standardized包含了标准化后的数据

通过上述代码，我们对DataFrame中的每一列执行了标准化处理，减去了该列的均值并除以了标准差，得到了新的标准化数据。

### 2.2.2 归一化的目的与实现

归一化是另一种数据预处理技术，其目的在于把数据缩放到一个特定的范围，通常是[0,1]区间内。归一化的公式如下：

\[ X_{\text{norm}} = \frac{(X - X_{\text{min}})}{(X_{\text{max}} - X_{\text{min}})} \]

其中，\(X\) 是原始数据，\(X_{\text{min}}\) 和 \(X_{\text{max}}\) 分别是数据中的最小值和最大值。

在Python中实现归一化的代码示例如下：

# 假设df为pandas DataFrame，并且我们需要归一化df中的所有列
df_normalized = (df - df.min()) / (df.max() - df.min())

# df_normalized包含了归一化后的数据

通过执行上述代码，DataFrame中每一列的数据被缩放到了[0,1]区间内，完成了归一化过程。

## 2.3 特征选择与提取

### 2.3.1 筛选相关特征

在构建机器学习模型之前，特征选择是一个关键步骤，用以提高模型性能，缩短训练时间，并减少过拟合的风险。常用的特征选择方法有：

- 单变量统计测试，如卡方检验、ANOVA。
- 基于模型的特征选择，使用诸如递归特征消除（RFE）的方法。

### 2.3.2 提取高维数据特征

对于高维数据集，直接分析原始特征是不切实际的。特征提取技术可以用来降维，包括：

- 主成分分析（PCA）
- 线性判别分析（LDA）
- t-分布随机邻域嵌入（t-SNE）

这些技术能够帮助我们从数据中提取出最重要的特征，简化数据集，同时尽可能保留原始数据的信息。

# 3. princomp包与主成分分析

## 3.1 princomp包简介

### 3.1.1 princomp包的主要功能

princomp包是R语言中实现主成分分析（PCA）的一个常用工具包。PCA是一种统计技术，通过正交变换将一组可能相关的变量转换成一组线性不相关的变量，这些新的变量称为主成分。主成分按照方差递减的顺序排列，通常用于数据降维、可视化及噪声过滤。

在princomp包中，主要功能包括但不限于：
- 数据的标准化处理；
- 计算数据的协方差矩阵；
- 提取特征值和特征向量；
- 降维和生成得分（即主成分）。

### 3.1.2 如何安装和加载princomp包

首先，确保你已经安装了R语言，并且有一个可用的R环境。在R的控制台中，可以通过以下指令安装princomp包：

install.packages("princomp")

安装完成后，使用以下指令加载princomp包：

library(princomp)

## 3.2 使用princomp进行主成分分析

### 3.2.1 princomp函数的使用方法

princomp函数是执行主成分分析的核心函数。基本的使用方法如下：

pca_result <- princomp(x, cor = FALSE, scores = TRUE, ...)

- `x` 参数代表你想要分析的数据集，数据通常为数值型矩阵或数据框；