机器学习中的正则化艺术：吴恩达课程中的过拟合避免策略


# 摘要
本文全面解析了机器学习中正则化技术的理论基础及其在实践中的应用。首先，探讨了正则化的概念、目的和作用，特别是针对过拟合问题的解决方法及其与模型复杂度之间的关系。接着，详细介绍了L1、L2以及弹性网络等不同类型的正则化方法，并讨论了如何在不同场景下选择合适的正则化参数及其优化策略。第三章通过Python实践和案例研究，展示了正则化技术在具体模型中的应用和效果对比。第四章深入探讨了正则化的数学原理，包括与贝叶斯统计的联系、优化算法的结合，以及在深度学习中的应用。第五章展望了正则化技术的未来趋势，特别强调了集成学习和大规模数据集中的应用。最后，第六章通过一个构建正则化模型的项目实践，介绍了项目流程、数据准备、模型构建以及结果评估与优化。

# 关键字
机器学习；正则化；过拟合；模型选择；贝叶斯统计；深度学习

参考资源链接：[吴恩达机器学习课程PPT精华：数据挖掘与自适应程序](https://wenku.csdn.net/doc/646580fc543f844488aa500b?spm=1055.2635.3001.10343)
# 1. 机器学习与过拟合概念解析

在数据科学和机器学习的领域，模型的构建和优化是核心任务之一。本章节我们首先会对机器学习的概念进行解析，并进一步探讨过拟合这一在模型训练过程中经常出现的问题。

## 1.1 机器学习基础

机器学习是让计算机通过数据自动学习的科学和技术。它从历史数据中学习到规律，并将这些规律应用在新的数据上进行预测或决策。机器学习模型的性能直接关系到业务的成效，因此对模型的理解和掌握至关重要。

## 1.2 过拟合的定义

过拟合（Overfitting）是机器学习中一个常见且棘手的问题。简而言之，过拟合是指模型在训练数据上表现极好，但在新的、未见过的数据上表现糟糕的现象。这是因为模型学习到了训练数据中的噪声和非代表性的特征，而非普遍适用的模式。

## 1.3 过拟合的影响

过拟合会直接影响模型的泛化能力，导致模型在实际应用中的表现远低于预期。在商业环境中，这可能会导致错误的预测或决策，进而产生严重的财务损失或其他不良后果。

通过理解这些基础概念，我们将为后续章节中深入探讨如何使用正则化技术来应对过拟合问题奠定坚实的基础。在下一章中，我们将详细介绍正则化技术，并解释它是如何帮助我们避免过拟合的。

# 2. 正则化技术理论基础

### 2.1 正则化的目的和作用

正则化是在机器学习中防止过拟合的重要技术。它通过向损失函数添加一个额外的项来惩罚模型复杂度，从而达到提高模型泛化能力的目的。正则化的核心思想是“少即是多”，即在保持模型对训练数据具有足够拟合度的同时，尽量减少模型参数的数量和大小，使得模型结构尽可能简单，避免对训练数据中的噪声过度敏感。

#### 2.1.1 解决过拟合问题

过拟合是指模型在训练数据上表现良好，但在新的、未见过的数据上表现差的现象。这通常是因为模型学习了训练数据中的特定噪声和异常值，而没有捕捉到数据的真实分布。正则化通过对模型的复杂度进行约束，减少了模型对这些噪声和异常值的依赖，从而减少了过拟合的风险。

正则化通常有两种形式：L1和L2，它们通过不同的方式对模型复杂度进行惩罚。L1正则化倾向于产生稀疏模型，因为它倾向于将参数值压缩到0，而L2正则化则倾向于分散参数值，但不会完全消除任何一个参数。在实际应用中，选择哪种形式取决于特定的问题和数据集。

#### 2.1.2 正则化与模型复杂度

模型复杂度是衡量模型拟合数据能力的一个重要指标。复杂度高的模型可能会对训练数据过拟合，而复杂度低的模型可能会欠拟合。正则化通过添加惩罚项来控制模型复杂度，使得模型在保持对数据拟合能力的同时，避免过度拟合。

### 2.2 正则化方法分类

正则化方法大致可以分为L1正则化、L2正则化和弹性网络三类。这些方法通过不同的数学形式对模型参数施加惩罚，以达到抑制过拟合的目的。

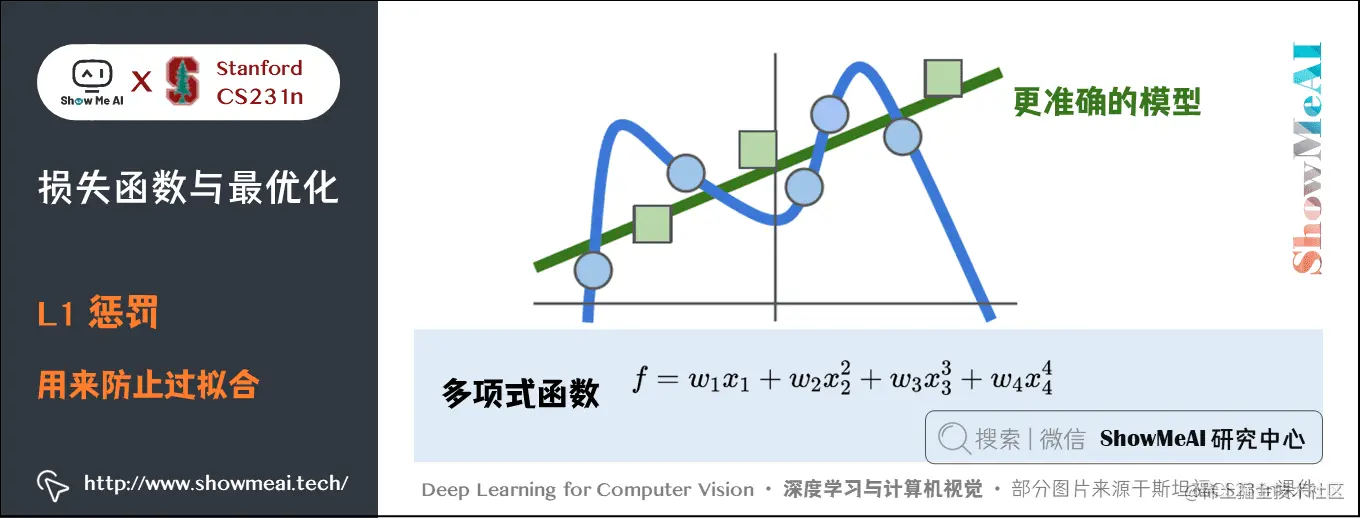
#### 2.2.1 L1正则化（Lasso）

L1正则化，也被称为Lasso，是一种对模型参数大小施加惩罚的方法。其对数损失函数的惩罚项是所有参数的绝对值之和。L1正则化的主要优点是它倾向于产生稀疏的模型，即它能够将一些不重要的特征参数压缩到零，从而实现特征选择的目的。

L1正则化的一个关键挑战是选择合适的正则化参数（通常用λ表示）。选择过大的λ会导致重要特征的参数也被错误地压缩到零，而选择过小的λ则无法有效抑制过拟合。L1正则化的优化问题通常通过坐标下降法（Coordinate Descent）等迭代算法解决。

#### 2.2.2 L2正则化（Ridge）

L2正则化，也被称为Ridge回归，通过在损失函数中添加参数平方和的惩罚项来实现。与L1正则化不同，L2正则化不会将参数压缩到零，因此不会产生稀疏模型。它的主要优点是倾向于使参数值分散且较小，从而减少模型对单个参数的依赖，防止过拟合。

L2正则化同样需要选择一个合适的正则化参数λ。通常，λ选择过大可能会导致模型欠拟合，而选择过小则可能无法有效控制模型复杂度。L2正则化问题的解通常通过对正则化后的损失函数求导并解线性方程来获得。

#### 2.2.3 弹性网络（Elastic Net）

弹性网络是L1正则化和L2正则化的一种结合形式，它将两者的优势结合起来，以期获得更好的特征选择和模型泛化能力。弹性网络的惩罚项是L1和L2正则化项的线性组合，其可以控制模型的稀疏性和参数的大小。

弹性网络的关键在于平衡L1和L2正则化项的权重。一般来说，这种平衡由参数α决定，其中α = 1表示纯L1正则化，α = 0表示纯L2正则化。参数α和正则化参数λ的选择对于模型的最终性能至关重要。

### 2.3 正则化强度与模型选择

模型的选择依赖于特定问题的需求以及数据集的特性。正则化强度的选择是一个关键因素，它决定了模型复杂度和泛化能力之间的平衡。

#### 2.3.1 如何选择合适的正则化参数

选择合适的正则化参数是防止过拟合的关键。参数选择的过程通常需要使用验证集或交叉验证方法。在L1和L2正则化中，通常使用网格搜索（Grid Search）来遍历一系列可能的参数值，并评估模型在验证集上的性能，最终选择使得验证集误差最小的参数值。

#### 2.3.2 正则化参数的优化策略

正则化参数的优化策略不仅包括确定合适的λ值，还涉及对模型结构的调整和选择。例如，选择包含或不包含截距项、选择特征变量的类型和数量等。此外，正则化参数的选择应结合模型的优化算法，如随机梯度下降（Stochastic Gradient Descent）或批量梯度下降（Batch Gradient Descent）等。

选择正则化参数的策略需要综合考虑模型的复杂度、计算资源和预期的泛化误差。在实际应用中，可能需要多次迭代和调整参数，以便在保持模型性能的同时，控制计算成本。

from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
import numpy as np

# 假设X_train, y_train为已有的训练数据和标签
# 创建Ridge回归模型实例
ridge_model = Ridge()

# 设定正则化参数的搜索范围
parameters = {'alpha': np.logspace(-4, 4, 100)}

# 使用交叉验证来选择最佳的正则化参数
clf = GridSearchCV(ridge_model, parameters, scoring='neg_mean_squared_error', cv=5)
clf.fit(X_train, y_train)

# 输出最佳的参数和对应的模型性能
print("最优正则化参数:", clf.best_params_)
print("模型在验证集上的性能:", -clf.best_score_)

在上述代码块中，我们使用了`GridSearchCV`来对`Ridge`回归模型进行网格搜索，以确定最佳的正则化参数。我们遍历了从10^-4到10^4的正则化参数范围，并通过五折交叉验证来评估每个参数值对应的模型性能。

以上内容仅以Ridge回归为例，同样的方法也适用于Lasso回归和Elastic Net模型。对于L1正则化，还需要考虑算法的选择，例如可以使用`LassoCV`类，它内置了交叉验证功能，从而避免了手动设置网格搜索的步骤。

在接下来的章节中，我们将继续深入探讨正则化技术在实践中的应用和具体案例分析。

# 3. 正则化实践技巧与案例分析

在深入理解正则化的理论基础之后，我们现在将目光转向实践技巧，这是将正则化技术应用到具体机器学习问题中的关键步骤。本章节将提供正则化技术的实现方法、不同模型中的应用案例，以及通过案例研究展示过拟合与正则化之间的关系和实际影响。

## 3.1 基于Python的正则化实现

Python作为机器学习领域的主流编程语言之一，其丰富的库支持使得实现正则化变得简单而直观。我们将使用Python中的scikit-learn库来演示如何轻松地实现正则化，并对参数进行调整和验证。

### 3.1.1 使用scikit-learn库进行正则化

scikit-learn库提供了易于使用的接口来实现正则化。我们将演示如何在构建线性回归和逻辑回归模型时应用L1和L2正则化。

from sklearn.linear_model import Lasso, Ridge, ElasticNet, LogisticRegression
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 生成模拟数据集
X, y = make_classification(n_samples=1000, n_features=20, n_informative=2, n_redundant=10, random_state=42)
X_train, X_test, y_train, y_test = tra