线性化在金融科技中的应用：提升金融交易的可靠性和可审计性

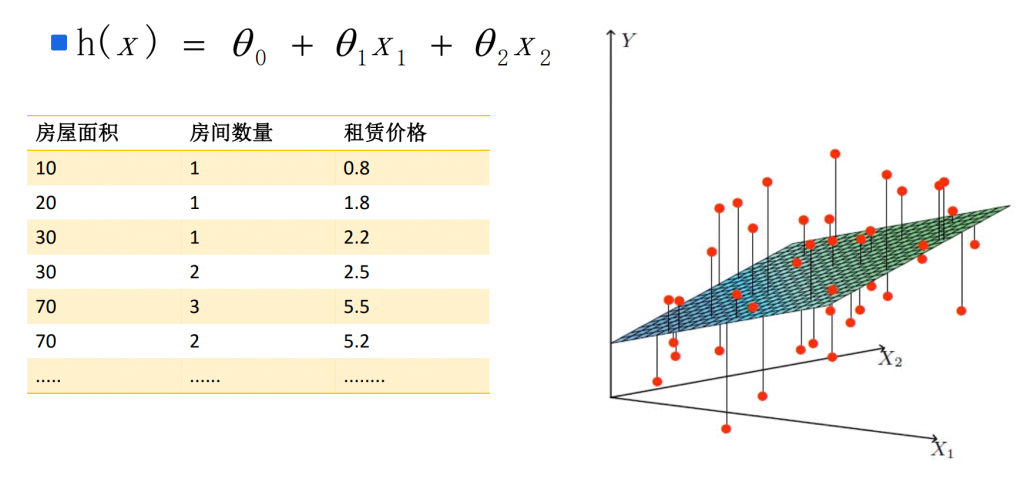
# 1. 线性化的概念和原理**

线性化是一种数学技术，用于将非线性问题近似为线性问题。在金融科技中，线性化被广泛应用于各种领域，因为它可以简化复杂的问题，并使我们能够使用线性代数和优化技术来解决这些问题。

线性化的基本原理是使用泰勒级数展开式在非线性函数的某个点附近对其进行近似。通过截断泰勒级数展开式的高阶项，我们可以得到非线性函数的线性近似。这种线性近似可以用来近似非线性问题的行为，并使我们能够使用线性方法来解决这些问题。

# 2. 线性化在金融科技中的应用

### 2.1 线性化模型在金融交易中的应用

#### 2.1.1 交易风险评估

线性化模型在金融交易风险评估中发挥着至关重要的作用。通过将复杂的非线性交易数据线性化，模型可以识别潜在的风险因素并量化其影响。具体而言，线性化模型可以：

- **识别风险因素：**通过线性回归或逻辑回归等技术，模型可以识别与交易风险相关的关键因素，例如市场波动、交易规模和交易对手信用评级。
- **量化风险敞口：**线性模型可以计算每个风险因素对交易风险的贡献程度，从而量化交易的整体风险敞口。
- **预测风险事件：**通过训练线性分类器，模型可以预测交易是否会发生风险事件，例如违约或亏损。

#### 2.1.2 交易策略优化

线性化模型还可以用于优化金融交易策略。通过模拟不同交易策略在各种市场条件下的表现，模型可以帮助交易员识别最优策略并提高交易收益。具体而言，线性化模型可以：

- **模拟交易策略：**模型可以模拟不同交易策略在历史或模拟市场数据上的表现，评估其收益率、风险和夏普比率。
- **优化策略参数：**通过线性规划或其他优化技术，模型可以优化交易策略的参数，例如交易频率、持仓时间和止损水平，以最大化收益或最小化风险。
- **回测交易策略：**模型可以对优化后的交易策略进行回测，以评估其在真实市场条件下的表现并识别潜在的改进领域。

### 2.2 线性化算法在金融数据分析中的应用

#### 2.2.1 金融数据降维

金融数据通常具有高维和复杂性。线性化算法可以将高维数据降维到低维空间，从而简化数据分析和可视化。具体而言，线性化算法可以：

- **主成分分析（PCA）：**PCA是一种线性化算法，通过识别数据中的主成分来将数据降维。主成分是数据方差最大的线性组合，可以捕捉数据的大部分信息。
- **奇异值分解（SVD）：**SVD是一种线性化算法，通过将数据分解为奇异值、左奇异向量和右奇异向量的乘积来降维。SVD可以有效地处理稀疏和噪声数据。

#### 2.2.2 金融数据预测

线性化算法还可以用于预测金融数据，例如股票价格、汇率和利率。通过学习历史数据中的线性关系，模型可以预测未来趋势和做出准确的预测。具体而言，线性化算法可以：

- **线性回归：**线性回归是一种线性化算法，通过拟合数据点之间的直线来预测连续变量。线性回归可以用于预测股票价格、汇率和利率等金融变量。
- **时间序列分析：**时间序列分析是一种线性化算法，通过分析时间序列数据的趋势和季节性来预测未来值。时间序列分析可以用于预测股票价格、商品价格和经济指标。

# 3. 线性化模型的实践应用

### 3.1 线性回归模型在金融交易预测中的应用

#### 3.1.1 模型构建与训练

线性回归模型是一种用于预测连续型变量的统计模型。在金融交易预测中，线性回归模型可以用来预测未来资产价格、交易量或其他相关指标。

模型构建过程如下：

1. **数据收集：**收集历史